山东省济南市历城区2022-2023学年九年级上学期12月月考数学试题
试卷更新日期:2022-12-27 类型:月考试卷
一、单选题
-
1. 如图是一根空心方管,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是( ) .A、 B、 C、 D、3. 在一个不透明的布袋中装有50个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.3左右,则布袋中白球可能有( )A、15个 B、20个 C、30个 D、35个4. 若关于x的一元二次方程有实数根,则实数k的取值范围是( )A、 B、且 C、 D、5. 若A(﹣3,y1), ,C(2,y3)在二次函数y=x2+2x+c的图象上,则y1 , y2 , y3的大小关系是( )A、y2<y1<y3 B、y1<y3<y2 C、y1<y2<y3 D、y3<y2<y16. 如图,AB是⊙O的直径,点D在⊙O上,若∠AOC=120°,则∠D的度数是( )
2. 已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是( ) .A、 B、 C、 D、3. 在一个不透明的布袋中装有50个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.3左右,则布袋中白球可能有( )A、15个 B、20个 C、30个 D、35个4. 若关于x的一元二次方程有实数根,则实数k的取值范围是( )A、 B、且 C、 D、5. 若A(﹣3,y1), ,C(2,y3)在二次函数y=x2+2x+c的图象上,则y1 , y2 , y3的大小关系是( )A、y2<y1<y3 B、y1<y3<y2 C、y1<y2<y3 D、y3<y2<y16. 如图,AB是⊙O的直径,点D在⊙O上,若∠AOC=120°,则∠D的度数是( )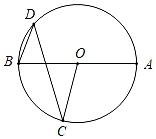 A、20° B、30° C、40° D、45°7. 如图,点 , , ,在 上, 是 的一条弦,则 ( ).
A、20° B、30° C、40° D、45°7. 如图,点 , , ,在 上, 是 的一条弦,则 ( ). A、 B、 C、 D、8. 如图,当ab>0时,函数y=ax2与函数y=bx+a的图象大致是( )A、
A、 B、 C、 D、8. 如图,当ab>0时,函数y=ax2与函数y=bx+a的图象大致是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,在平面直角坐标系中,在中,点在轴上, , 函数的图象经过点与边的中点 , 则的值为( )
9. 如图,在平面直角坐标系中,在中,点在轴上, , 函数的图象经过点与边的中点 , 则的值为( ) A、24 B、 C、36 D、10. 已知函数(a为常数),当时,y随x增大而增大.是该函数图象上的两点,对任意的和 , 总满足 , 则实数a的取值范围是( )A、 B、 C、 D、
A、24 B、 C、36 D、10. 已知函数(a为常数),当时,y随x增大而增大.是该函数图象上的两点,对任意的和 , 总满足 , 则实数a的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 如图,在中, , , , , 则的长 .
 12. 将抛物线先向右平移2个单位,再向上平移3个单位后,得到新抛物线的表达式是 .13. 育才学校积极开展志愿者服务活动,来自初三的3名同学(1男2女)组成了“关爱老人”志愿小分队.若从该小分队中任选2名同学参加周末的志愿活动,则恰好是1男1女的概率是 .14. 如图,菱形的对角线相交于点O,点E在上,连接 , 点F为的中点,连接 , 若 , , , 则线段的长为 .
12. 将抛物线先向右平移2个单位,再向上平移3个单位后,得到新抛物线的表达式是 .13. 育才学校积极开展志愿者服务活动,来自初三的3名同学(1男2女)组成了“关爱老人”志愿小分队.若从该小分队中任选2名同学参加周末的志愿活动,则恰好是1男1女的概率是 .14. 如图,菱形的对角线相交于点O,点E在上,连接 , 点F为的中点,连接 , 若 , , , 则线段的长为 .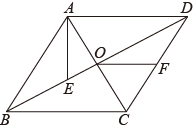 15. 如图,为等腰直角三角形, , , 与相切于 , 则图中阴影部分的面积是 .
15. 如图,为等腰直角三角形, , , 与相切于 , 则图中阴影部分的面积是 . 16. 如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为 .
16. 如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为 .
三、解答题
-
17. 计算:18. 解方程:19. 如图,矩形ABCD中,点M在DC上,AM=AB,且BN⊥AM,垂足为N,证明:△ABN≌△MAD;
 20. 在中国共青团成立一百周年之际,某校举行了以“青春心向党,建功新时代”为主题的知识竞赛活动.发现该校全体学生的竞赛成绩(百分制)均不低于60分,现从中随机抽取n名学生的竞赛成绩进行整理和分析(成绩得分用x表示,共分成四组),并绘制成如下的竞赛成绩分组统计表和扇形统计图.“”这组的数据如下:90,92,93,95,95,96,96,96,97,100.
20. 在中国共青团成立一百周年之际,某校举行了以“青春心向党,建功新时代”为主题的知识竞赛活动.发现该校全体学生的竞赛成绩(百分制)均不低于60分,现从中随机抽取n名学生的竞赛成绩进行整理和分析(成绩得分用x表示,共分成四组),并绘制成如下的竞赛成绩分组统计表和扇形统计图.“”这组的数据如下:90,92,93,95,95,96,96,96,97,100.竞赛成绩分组统计表
组别
竞赛成绩分组
频数
平均分
1
8
65
2
a
75
3
b
88
4
10
95

请根据以上信息,解答下列问题:
(1)、a=;(2)、“”这组数据的众数是分;(3)、扇形统计图中第3组对应圆心角为;(4)、若学生竞赛成绩达到96分以上(含96分)获奖,请你估计全校1200名学生中获奖的人数.21. 开封清明上河园是依照北宋著名画家张择端的《清明上河图》建造的,拂云阁是园内最高的建筑.某数学小组测量拂云阁DC的高度,如图,在A处用测角仪测得拂云阁顶端D的仰角为34°,沿AC方向前进15m到达B处,又测得拂云阁顶端D的仰角为45°.已知测角仪的高度为1.5m,测量点A,B与拂云阁DC的底部C在同一水平线上,求拂云阁DC的高度(结果精确到1m.参考数据: , , ). 22. 某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中 , 且x为整数).当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天的销售量为95件.(1)、求y与x之间的函数关系式.(2)、设该商店销售这种消毒用品每天获利w(元),当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?23. 如图,已知是⊙O的直径,C为⊙O上一点,的平分线交⊙O于点D,过点D作⊙O的切线交的延长线于点E.
22. 某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中 , 且x为整数).当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天的销售量为95件.(1)、求y与x之间的函数关系式.(2)、设该商店销售这种消毒用品每天获利w(元),当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?23. 如图,已知是⊙O的直径,C为⊙O上一点,的平分线交⊙O于点D,过点D作⊙O的切线交的延长线于点E.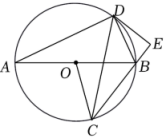 (1)、求证:;(2)、若 , , 求DE的长.24. 如图,一次函数与反比例函数的图象交于点和 , 与y轴交于点C.
(1)、求证:;(2)、若 , , 求DE的长.24. 如图,一次函数与反比例函数的图象交于点和 , 与y轴交于点C. (1)、 , ;(2)、过点A作轴于点D,点P是反比例函数在第一象限的图象上一点,设直线与线段交于点E,当时,求点P的坐标.(3)、点M是坐标轴上的一个动点,点N是平面内的任意一点,当四边形是矩形时,求出点M的坐标.25. 在中, , 点D,E分别是的中点,点P是射线上一点,连接 , 将线段绕点P顺时针旋转得到线段 , 连接 .
(1)、 , ;(2)、过点A作轴于点D,点P是反比例函数在第一象限的图象上一点,设直线与线段交于点E,当时,求点P的坐标.(3)、点M是坐标轴上的一个动点,点N是平面内的任意一点,当四边形是矩形时,求出点M的坐标.25. 在中, , 点D,E分别是的中点,点P是射线上一点,连接 , 将线段绕点P顺时针旋转得到线段 , 连接 .

 (1)、问题发现
(1)、问题发现如图(1),当点P与点D重合时,线段与的数量关系是 , .
(2)、探究证明当点P在射线上运动时(不与点E重合),(1)中结论是否一定成立?请仅就图(2)中的情形给出证明.
(3)、问题解决若 , 连接 , 当是等边三角形时,直接写出的长度.
26. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交点C,抛物线过A,C两点,与x轴交于另一点B.
 (1)、求抛物线的解析式.(2)、在直线上方的抛物线上有一动点E,连接 , 与直线相交于点F,当时,求E点坐标.(3)、在(2)的条件下,若点E位于对称轴左侧,点M是抛物线对称轴上一点,点N是抛物线上一点,当以M,N,E,B为顶点的四边形是菱形时,直接写出点M的坐标.
(1)、求抛物线的解析式.(2)、在直线上方的抛物线上有一动点E,连接 , 与直线相交于点F,当时,求E点坐标.(3)、在(2)的条件下,若点E位于对称轴左侧,点M是抛物线对称轴上一点,点N是抛物线上一点,当以M,N,E,B为顶点的四边形是菱形时,直接写出点M的坐标.