辽宁省抚顺市新抚区2022-2023学年九年级上学期质量检测（一）数学试题

试卷更新日期：2022-12-27 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列方程中，关于x的一元二次方程是（）

A、x²-x（x＋3）＝0 B、ax²＋bx＋c＝0 C、x²-2x＋3＝0 D、x²-2y-1＝0

查看试题解析
2. 一元二次方程 $4 x^{2} - 6 x + 1 = 0$ 的二次项系数、一次项系数、常数项分别是（）

A、4，6，1 B、4，6，－1 C、4，－6，1 D、4，－6，－1

查看试题解析
3. 已知关于x的一元二次方程 $x^{2} + 3 x - m = 0$ 的一个根是 $x = 1$ ，则m的值为（）

A、2 B、4 C、-4 D、-2

查看试题解析
4. 抛物线 $y = {(x + 1)}^{2} + 2$ 的顶点坐标为（）

A、（－1，2） B、（1，2） C、（1，－2） D、（2，1）

查看试题解析
5. 用配方法解方程 $x^{2} + 4 x + 1 = 0$ ，下列变形正确的是（）

A、 ${(x + 2)}^{2} = - 5$ B、 ${(x + 2)}^{2} = 5$ C、 ${(x + 2)}^{2} = - 3$ D、 ${(x + 2)}^{2} = 3$

查看试题解析
6. 若点 $A (- 4 ， y_{1})$ ， $B (- 1 ， y_{2})$ ， $C (1 ， y_{3})$ 都是二次函数 $y = x^{2} + 4 x + k$ 的图象上的点，则（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{3} < y_{2} < y_{1}$ D、 $y_{3} < y_{1} < y_{2}$

查看试题解析
7. 函数y＝ax－a和 $y = a x^{2} + 2$ （a为常数，且 $a \neq 0$ ），在同一平面直角坐标系中的大致图象可能是（）

A、 B、 C、 D、

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ，将 $△ A B C$ 绕点A顺时针旋转 $90 °$ 后得到 $△ A B^{'} C^{'}$ （点B的对应点是点 $B^{'}$ ，点C的对应点是点 $C^{'}$ ），连接 $C C^{'}$ ，若 $∠ B = 80 °$ ，则 $∠ C C^{'} B^{'}$ 的大小是（）

A、25° B、30° C、35° D、40°

查看试题解析
9. 如图是由三个边长分别为6、9、x的正方形所组成的图形，若直线AB将它分成面积相等的两部分，则x的值是（）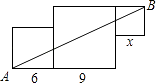

A、1或9 B、3或5 C、4或6 D、3或6

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的部分图像如图，图像过点 $(- 1 ， 0)$ ，对称轴为直线 $x = 2$ ，下列结论：① $4 a + b = 0$ ；② $9 a + c > 3 b$ ；③ $6 a + b + 2 c > 0$ ；④ $5 a + c = 0$ ；⑤当 $x > - 1$ 时， $y$ 的值随 $x$ 值的增大而增大．其中正确的结论有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 一元二次方程x²﹣x＝0的根是．

查看试题解析
12. 抛物线 $y = x^{2} - 2 x - 3$ 与x轴交点坐标是．

查看试题解析
13. 抛物线 $y = 2 {(x + 3)}^{2} - 1$ 的对称轴是．

查看试题解析
14. 若关于x的一元二次方程 $x^{2} - 4 x + m - 1 = 0$ 有两个不相等的实数根，则m的取值范围是．

查看试题解析
15. 已知二次函数 $y = x^{2} - 2 x + 1$ ，当 $- 5 ⩽ x ⩽ 3$ 时，y的取值范围是．

查看试题解析
16. 已知点 $P (m + n ， - 2)$ 与点 $(1 ， m - n)$ 关于原点对称，则mn= ．

查看试题解析
17. 如图，正方形 $A B C D$ 中，将边 $A B$ 绕着点A旋转，当点B落在边 $C D$ 的垂直平分线上的点E处时， $∠ B E D$ 的度数为．

查看试题解析
18. 如图，在 $△ A B C$ 中， $A B = \sqrt{2}$ ， $A C = 4$ ，以 $C$ 为旋转中心，将线段 $C B$ 顺时针旋转 $90 °$ 得线段 $C D$ ，连接 $A D$ ，则 $A D$ 的最小值为．

查看试题解析

三、解答题

19. 如图，四边形 $A B C D$ 四个顶点的坐标分别是 $A (- 2 ， - 1)$ ， $B (- 2 ， - 2)$ ， $C (1 ， - 3)$ ， $D (1 ， 1)$ ，将四边形 $A B C D$ 绕点O顺时针旋转90°得四边形 $A_{1}^{} B_{1}^{} C_{1}^{} D_{1}^{}$ ，

(1)、画出四边形 $A_{1}^{} B_{1}^{} C_{1}^{} D_{1}^{}$ ，写出 $A_{1}$ ， $B_{1}$ ， $C_{1}$ ， $D_{1}$ 的坐标；

(2)、直接写出四边形 $A B C D$ 与四边形 $A_{1}^{} B_{1}^{} C_{1}^{} D_{1}^{}$ 重叠部分的面积．

查看试题解析
20. 解方程：

(1)、 $4 {(x + 1)}^{2} - 9 {(x - 2)}^{2} = 0$ ；

(2)、 $2 x^{2} - 4 x - 1 = 0$ （配方法）．

查看试题解析
21. 画函数 $y = (x - 2)^{2} - 1$ 的图像，并根据图像回答：

(1)、当x为何值时，y随x的增大而减小；

(2)、当x为何值时， $y ＞ 0$ ；

(3)、当 $x \geq 0$ 时，y的取值范围是什么？

查看试题解析
22. 某连锁超市花2000元购进一批糖果，按80%的利润定价无人购买，决定降价出售，但仍无人购买，结果又一次降价后才售完，销售此糖果共获利916元，若两次降价的百分率相同，问每次降价的百分率是多少？

查看试题解析
23. 如图，已知 $△ A B C$ 中， $∠ C A B = 20 °$ ， $∠ A B C = 30 °$ ，将 $△ A B C$ 绕 $A$ 点逆时针旋转 $50 °$ 得到 $△ A B^{'} C^{'}$ ，

(1)、求证： $A C ∥ C^{'} B^{'}$ ；

(2)、求 $∠ B C C^{'}$ 的度数．

查看试题解析
24.
某超市对进货价为10元/千克的某种苹果的销售情况进行统计，发现每天销售量y（千克）与销售价x（元/千克）存在一次函数关系，如图所示．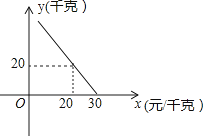

(1)、求y关于x的函数关系式（不要求写出x的取值范围）；

(2)、应怎样确定销售价，使该品种苹果的每天销售利润最大？最大利润是多少？

查看试题解析
25. 如图1，在 $△ A C B$ 中， $∠ A C B = 90 °$ ， $C A = C B$ ，点 $D ， E$ 分别在边 $C A ， C B$ 上， $C D = C E$ ，连接 $D E ， A E ， B D$ ，过点 $C$ 作 $C F ⊥ A E$ ，垂足为 $H$ ，直线 $C F$ 交直线 $B D$ 于 $F$ ．

(1)、求证： $D F = B F$ ；

(2)、将图1中的 $△ C D E$ 绕点 $C$ 逆时针旋转，其他条件不变，如图2，（1）的结论是否成立？如果成立，请证明；如果不成立，请说明理由；

(3)、若 $C D = 2$ ， $C B = 4$ ，将 $△ C D E$ 绕点 $C$ 逆时针旋转一周，当 $A ， E ， D$ 三点共线时，直接写出 $C F$ 的长．

查看试题解析
26. 如图，直线 $y = k x$ 与抛物线 $y = x^{2} + c$ 交于A，B两点，其中点B的坐标是 $(2 ， 2)$

(1)、求直线 $A B$ 及抛物线的解析式；

(2)、C为抛物线上的一点， $△ A B C$ 的面积为3，求点C的坐标；

(3)、P在抛物线上，Q在直线 $A B$ 上，M在坐标平面内，当以A，P，Q，M为顶点的四边形为正方形时，直接写出点M的坐标．

查看试题解析