广东省佛山市南海区大沥镇2022-2023学年九年级上学期第13周阶段考试(月考)数学试卷
试卷更新日期:2022-12-27 类型:月考试卷
一、单选题
-
1. 已知 , 且 , 则 , 一定满足( )A、 , B、 , C、 D、2. 下列方程中,没有实数根的是( )A、 B、 C、 D、3. 有三张卡片,正面分别写有、、三个字母,其它完全相同,反扣在桌面上混合均匀,从中在取两张,同时取到、的概率是( )A、 B、 C、 D、4. 如图,点E、F、G、H分别是四边形ABCD四条边的中点,要使四边形EFGH为菱形,四边形ABCD应具备的条件是( )
 A、一组对边平行而另一组对边不平行 B、对角线相等 C、对角线互相垂直 D、对角线互相平分5. 如图,有一面积为的长方形鸡场,鸡场的一边靠墙(墙长),另三边用竹篱笆围成,其中一边开有的门,竹篱笆的总长为 . 设鸡场垂直于墙的一边为 , 则列方程正确的是( )
A、一组对边平行而另一组对边不平行 B、对角线相等 C、对角线互相垂直 D、对角线互相平分5. 如图,有一面积为的长方形鸡场,鸡场的一边靠墙(墙长),另三边用竹篱笆围成,其中一边开有的门,竹篱笆的总长为 . 设鸡场垂直于墙的一边为 , 则列方程正确的是( ) A、 B、 C、 D、6. 如图,点P在的边上,添加如下一个条件后,仍不能得到的是( )
A、 B、 C、 D、6. 如图,点P在的边上,添加如下一个条件后,仍不能得到的是( ) A、 B、 C、 D、7. 在阳光的照射下,一个矩形框的影子的形状不可能是( )A、线段 B、平行四边形 C、等腰梯形 D、矩形8. 若关于x的一元二次方程有解,那么m的取值范围是( )A、 B、 C、且 D、且9. 下列命题中正确的是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相垂直平分且相等的四边形是正方形 D、一组对边相等,另一组对边平行的四边形是平行四边形10. 如图,在中,中线、相交于点F,连接 , 则下列结论:① , ② , ③ , ④ . 其中正确结论的个数是( )
A、 B、 C、 D、7. 在阳光的照射下,一个矩形框的影子的形状不可能是( )A、线段 B、平行四边形 C、等腰梯形 D、矩形8. 若关于x的一元二次方程有解,那么m的取值范围是( )A、 B、 C、且 D、且9. 下列命题中正确的是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相垂直平分且相等的四边形是正方形 D、一组对边相等,另一组对边平行的四边形是平行四边形10. 如图,在中,中线、相交于点F,连接 , 则下列结论:① , ② , ③ , ④ . 其中正确结论的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 已知关于的方程的一个根为 , 则方程的另一个根 .12. 在一个不透明的盒子里,装有5个黑球和若干个白球,这些球除颜色外都相同,将其摇匀后从中随机摸出一个球,记下颜色后再把它放回盒子中,不断重复,共摸球40次,其中10次摸到黑球,估计盒子中白球的个数是 .13. 如图,菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高DH= .
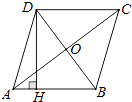 14. 如图,和是以点O为位似中心的位似图形.若 , 则与的面积比是 .
14. 如图,和是以点O为位似中心的位似图形.若 , 则与的面积比是 . 15. 如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD= .
15. 如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD= .
三、解答题
-
16. 解方程: .17. 一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)、求摸出1个球是白球的概率;(2)、摸出1个球,记下颜色后放回,并搅匀,再摸出1个球,求两次摸出的球恰好颜色不同的概率(要求画树状图或列表).
18. 如图,在路灯下,小明(用线段表示)的影子是 , 在处有一棵大树(用线段表示),它的影子是 .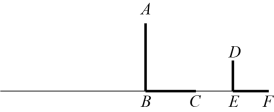 (1)、请确定路灯的位置(用点表示);(2)、若身高1.6米的小明的影长3米,他在距离灯的底部18米处,求路灯的高度.19. 如图,在平行四边形中,对角线相交于点O,且 .
(1)、请确定路灯的位置(用点表示);(2)、若身高1.6米的小明的影长3米,他在距离灯的底部18米处,求路灯的高度.19. 如图,在平行四边形中,对角线相交于点O,且 . (1)、求证:四边形是矩形;(2)、若 , , 求的长.20. 如图,中 , , 点、分别在的边、上,且 .
(1)、求证:四边形是矩形;(2)、若 , , 求的长.20. 如图,中 , , 点、分别在的边、上,且 . (1)、求证: .(2)、如果 , , , 求的长.21. 某工厂生产一批小家电,2020年的出厂价是144元,2021年、2022年连续两年改进技术,降低成本,2022年出厂价调整为100元.(1)、这两年出厂价下降的百分比相同,求平均下降率.(结果保留2位小数)(2)、某商场今年销售这批小家电的售价为140元时,平均每天可销售20台,为了减少库存,商场决定降价销售,经调查发现小家电单价每降低5元,每天可多售出10台,如果每天盈利1250元,单价应降低多少22. 如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)、求证: .(2)、如果 , , , 求的长.21. 某工厂生产一批小家电,2020年的出厂价是144元,2021年、2022年连续两年改进技术,降低成本,2022年出厂价调整为100元.(1)、这两年出厂价下降的百分比相同,求平均下降率.(结果保留2位小数)(2)、某商场今年销售这批小家电的售价为140元时,平均每天可销售20台,为了减少库存,商场决定降价销售,经调查发现小家电单价每降低5元,每天可多售出10台,如果每天盈利1250元,单价应降低多少22. 如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG. (1)、求证:四边形EFDG是菱形;(2)、求证: ;(3)、若AG=6,EG=2 ,求BE的长.23. 如图,在平面直角坐标系中,A、B两点的坐标分别为(20,0)和(0,15),动点P从点A出发在线段AO上以每秒2cm的速度向原点O运动,动直线EF从x轴开始以每秒1cm的速度向上平行移动(即EF∥x轴),分别与y轴、线段AB交于点E、F,连接EP、FP,设动点P与动直线EF同时出发,运动时间为t秒.
(1)、求证:四边形EFDG是菱形;(2)、求证: ;(3)、若AG=6,EG=2 ,求BE的长.23. 如图,在平面直角坐标系中,A、B两点的坐标分别为(20,0)和(0,15),动点P从点A出发在线段AO上以每秒2cm的速度向原点O运动,动直线EF从x轴开始以每秒1cm的速度向上平行移动(即EF∥x轴),分别与y轴、线段AB交于点E、F,连接EP、FP,设动点P与动直线EF同时出发,运动时间为t秒. (1)、求t=9时,△PEF的面积;(2)、直线EF、点P在运动过程中,是否存在这样的t使得△PEF的面积等于40cm2?若存在,请求出此时t的值;若不存在,请说明理由;(3)、当t为何值时,△EOP与△BOA相似.
(1)、求t=9时,△PEF的面积;(2)、直线EF、点P在运动过程中,是否存在这样的t使得△PEF的面积等于40cm2?若存在,请求出此时t的值;若不存在,请说明理由;(3)、当t为何值时,△EOP与△BOA相似.