安徽省安庆市怀宁县2022-2023学年九年级上学期第三次月考数学试卷
试卷更新日期:2022-12-27 类型:月考试卷
一、单选题
-
1. 若= , 则的值为( )A、1 B、 C、 D、2. 在中, , 则cosB的值为( )A、 B、 C、 D、3. 抛物线的顶点坐标是( )A、 B、 C、 D、4. 如图,点A为边上的任意一点,作于点C,于点D,下列用线段比表示出的值,正确的是( )
 A、 B、 C、 D、5. 已知是锐角, , 则的值是( )A、 B、 C、 D、6. 如图,平行四边形中,对角线相交于点 , 点E是的中点,则与的面积比为( )
A、 B、 C、 D、5. 已知是锐角, , 则的值是( )A、 B、 C、 D、6. 如图,平行四边形中,对角线相交于点 , 点E是的中点,则与的面积比为( )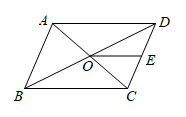 A、1:2 B、1:3 C、1:4 D、1:57. 若函数y=(a﹣1)x2﹣4x+2a的图象与x轴有且只有一个交点,则a的值为( ).A、-1 B、2 C、-1或2 D、-1或2或18. 在平面直角坐标系中,各顶点的坐标分别为: , 以O为位似中心,与位似,若B点的对应点的坐标为 , 则A点的对应点坐标为( )A、 B、 C、 D、9. 已知二次函数 , 若 , 且 , 则它的图象可能是( )A、
A、1:2 B、1:3 C、1:4 D、1:57. 若函数y=(a﹣1)x2﹣4x+2a的图象与x轴有且只有一个交点,则a的值为( ).A、-1 B、2 C、-1或2 D、-1或2或18. 在平面直角坐标系中,各顶点的坐标分别为: , 以O为位似中心,与位似,若B点的对应点的坐标为 , 则A点的对应点坐标为( )A、 B、 C、 D、9. 已知二次函数 , 若 , 且 , 则它的图象可能是( )A、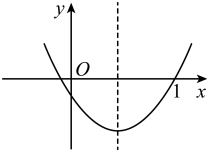 B、
B、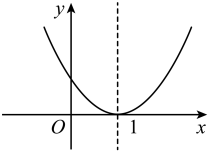 C、
C、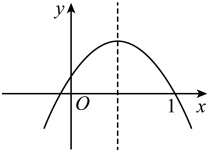 D、
D、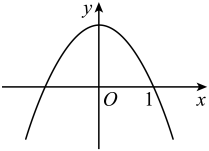 10. 如图,D是等边边上的一点,且 , 现将折叠,使点C与D重合,折痕为 , 点E、F分别在和上则( ).
10. 如图,D是等边边上的一点,且 , 现将折叠,使点C与D重合,折痕为 , 点E、F分别在和上则( ).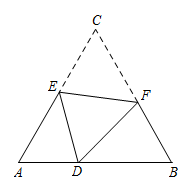 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 抛物线向左平移3个单位,所得的新抛物线的解析式为 .12. 已知舞台长 , 如果主持人从点A出发站到舞台的黄金分割点P处,且 , 那么主持人应走m(结果保留根号)13. 如图,点A、B分别在反比例函数、的图象上,且 , , 则
 14. 抛物线的对称轴为直线 ,(1)、a= .(2)、若抛物线在内与x轴只有一个交点,则t的取值范围是 .
14. 抛物线的对称轴为直线 ,(1)、a= .(2)、若抛物线在内与x轴只有一个交点,则t的取值范围是 .三、解答题
-
15. 计算:16. a,b,c为的三边长,且 , , 求的面积.17. 利民商店销售一种进价为50元/件的土特产商品,当售价为60元/件,每周可卖出200件,若每件商品的售价每上涨1元,则每周就会少卖10件.求利民商店将售价上涨多少时每周可获得最大利润?最大利润是多少?18. 已知:如图,在中,于D,E为直角边的中点,过D,E作直线交的延长线于F.求证: .
 19. 如图,一次函数的图像与轴、轴分别相交于 , 两点,且与反比例函数的图像在第一象限交于点 , 若 , 是线段的中点.
19. 如图,一次函数的图像与轴、轴分别相交于 , 两点,且与反比例函数的图像在第一象限交于点 , 若 , 是线段的中点. (1)、求一次函数和反比例函数的解析式.(2)、直接写出不等式的解集.20. 如图,某超市的仓储中心有一斜坡 , 其坡度为 , 顶部处的高 , B、C在同一水平地面上.
(1)、求一次函数和反比例函数的解析式.(2)、直接写出不等式的解集.20. 如图,某超市的仓储中心有一斜坡 , 其坡度为 , 顶部处的高 , B、C在同一水平地面上.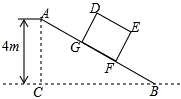 (1)、求斜坡长度;(2)、矩形为长方体货柜的侧面图,其中,将该货柜沿斜坡向上运送,此时 , 身高为的小明站在B处看到点D正上方处有一盏吊灯.求点D离地面的高度并求出小明的仰角的正切值.21. 如图,在平面直角坐标系中,抛物线的对称轴是直线 , 与x轴相交于两点(点在点的左侧),与轴交于点 .
(1)、求斜坡长度;(2)、矩形为长方体货柜的侧面图,其中,将该货柜沿斜坡向上运送,此时 , 身高为的小明站在B处看到点D正上方处有一盏吊灯.求点D离地面的高度并求出小明的仰角的正切值.21. 如图,在平面直角坐标系中,抛物线的对称轴是直线 , 与x轴相交于两点(点在点的左侧),与轴交于点 . (1)、求的值及直线的表达式;(2)、是第一象限内抛物线上的一点,过点作轴于点 , 交于点 . 当线段的长取最大值时,求点M的坐标.22. 为了在校园内有效开展劳动教育,东方红学校利用学校东南边靠墙的一块面积为单位1的的空地,把这块空地划分成七八九年级三个部分,如图,在中,点P是边上任意一点(点P与点B,C不重合),矩形的顶点F,E分别在上.七年级为矩形部分,八九年级为和两部分.
(1)、求的值及直线的表达式;(2)、是第一象限内抛物线上的一点,过点作轴于点 , 交于点 . 当线段的长取最大值时,求点M的坐标.22. 为了在校园内有效开展劳动教育,东方红学校利用学校东南边靠墙的一块面积为单位1的的空地,把这块空地划分成七八九年级三个部分,如图,在中,点P是边上任意一点(点P与点B,C不重合),矩形的顶点F,E分别在上.七年级为矩形部分,八九年级为和两部分.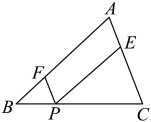 (1)、若 , 求;(2)、已知 . 设 , 矩形AFPE的面积为y,求y与x的函数关系式.(3)、在(2)的情形下,考虑实际情况,要求七年级所分面积最大.求出七年级所分矩形部分的面积在x为多少时取得最大值,并求出最大值是多少.23. 如图,设为锐角内一点, , 过点作 , , 连接 .
(1)、若 , 求;(2)、已知 . 设 , 矩形AFPE的面积为y,求y与x的函数关系式.(3)、在(2)的情形下,考虑实际情况,要求七年级所分面积最大.求出七年级所分矩形部分的面积在x为多少时取得最大值,并求出最大值是多少.23. 如图,设为锐角内一点, , 过点作 , , 连接 . (1)、求的度数;(2)、若 ,
(1)、求的度数;(2)、若 ,①连接 , 求证:;
②求的值.