2023年中考数学复习考点一遍过——一次函数
试卷更新日期:2022-12-26 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 如图是一次函数的图象,下列说法正确的是( )
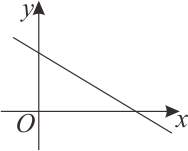 A、随增大而增大 B、图象经过第三象限 C、当时, D、当时,2. 根据图像,可得关于x的不等式的解集是( )
A、随增大而增大 B、图象经过第三象限 C、当时, D、当时,2. 根据图像,可得关于x的不等式的解集是( )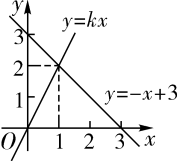 A、 B、 C、 D、3. 在平面直角坐标系中,一次函数y=-x+1的图象是( )A、
A、 B、 C、 D、3. 在平面直角坐标系中,一次函数y=-x+1的图象是( )A、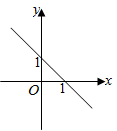 B、
B、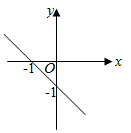 C、
C、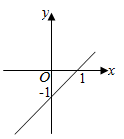 D、
D、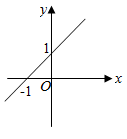 4. 若一次函数 的图象经过点 , ,则 与 的大小关系是( )A、 B、 C、 D、5. 点在正比例函数()的图象上,则k的值为( )A、-15 B、15 C、 D、6. 在平面直角坐标系中,将函数y=3x +2的图象向下平移3个单位长度,所得的函数的解析式是( )A、y=3x+5 B、y=3x﹣5 C、y=3x+1 D、y=3x﹣17. 如图,直线 分别与 轴、 轴交于点 和点 ,直线 分别与 轴、 轴交于点 和点 ,点 是 内部 (包括边上)的一点,则 的最大值与最小值之差为( )
4. 若一次函数 的图象经过点 , ,则 与 的大小关系是( )A、 B、 C、 D、5. 点在正比例函数()的图象上,则k的值为( )A、-15 B、15 C、 D、6. 在平面直角坐标系中,将函数y=3x +2的图象向下平移3个单位长度,所得的函数的解析式是( )A、y=3x+5 B、y=3x﹣5 C、y=3x+1 D、y=3x﹣17. 如图,直线 分别与 轴、 轴交于点 和点 ,直线 分别与 轴、 轴交于点 和点 ,点 是 内部 (包括边上)的一点,则 的最大值与最小值之差为( )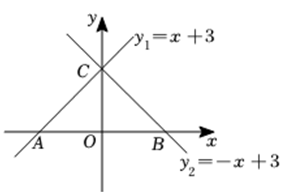 A、 B、 C、 D、8. 在同一平面直角坐标系中,一次函数与的图象如图所示,小星根据图象得到如下结论:
A、 B、 C、 D、8. 在同一平面直角坐标系中,一次函数与的图象如图所示,小星根据图象得到如下结论: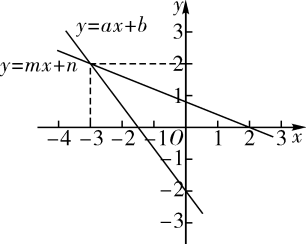
①在一次函数的图象中,的值随着值的增大而增大;②方程组的解为;③方程的解为;④当时,.
其中结论正确的个数是( )
A、1 B、2 C、3 D、49. 已知点 和点 都在正比例函数 图象上,则 的值为( )A、 B、 C、 D、10. 在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 将绕点逆时针旋转到如图的位置,的对应点恰好落在直线上,连接 , 则的长度为( )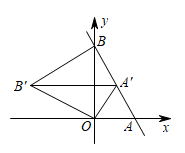 A、 B、 C、2 D、
A、 B、 C、2 D、二、填空题(每空3分,共30分)
-
11. 已知一次函数的图象经过点 , 则.12. 若一次函数y=kx+b的图象如图所示,则关于kx+b>0的不等式的解集为 .
 13. 如图,直线y1=k1x与直线y2=k2x+b交于点A(1,2).当y1<y2时,x的取值范围是 .
13. 如图,直线y1=k1x与直线y2=k2x+b交于点A(1,2).当y1<y2时,x的取值范围是 .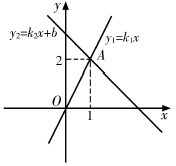 14. 已知直线y1=x-1与y2=kx+b相交于点(2,1).请写出b值(写出一个即可),使x>2时,y1>y2 .15. 已知直线y=kx+b过第一象限且函数值随着x的增大而减小,请列举出来这样的一条直线: .16. 点在一次函数的图像上,当时, , 则a的取值范围是 .17. 如图,点的坐标是(0,3),将沿轴向右平移至 , 点的对应点E恰好落在直线上,则点移动的距离是 .
14. 已知直线y1=x-1与y2=kx+b相交于点(2,1).请写出b值(写出一个即可),使x>2时,y1>y2 .15. 已知直线y=kx+b过第一象限且函数值随着x的增大而减小,请列举出来这样的一条直线: .16. 点在一次函数的图像上,当时, , 则a的取值范围是 .17. 如图,点的坐标是(0,3),将沿轴向右平移至 , 点的对应点E恰好落在直线上,则点移动的距离是 .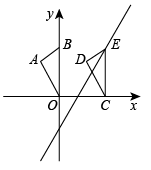 18. 如图,在平面直角坐标系xOy中,点A的坐标为(0,4),P是x轴上一动点,把线段PA绕点P顺时针旋转60°得到线段PF,连接OF,则线段OF长的最小值是 .
18. 如图,在平面直角坐标系xOy中,点A的坐标为(0,4),P是x轴上一动点,把线段PA绕点P顺时针旋转60°得到线段PF,连接OF,则线段OF长的最小值是 .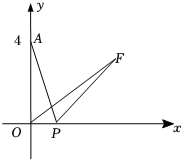 19. 已知一次函数y=3x-1与y=kx(k是常数,k≠0)的图象的交点坐标是(1,2),则方程组 的解是20. 某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为元(利润=总销售额-总成本).
19. 已知一次函数y=3x-1与y=kx(k是常数,k≠0)的图象的交点坐标是(1,2),则方程组 的解是20. 某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为元(利润=总销售额-总成本).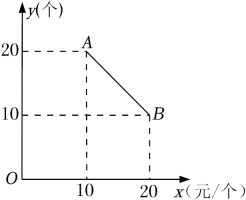
三、综合题(共6题,共60分)
-
21. 为改善村容村貌,阳光村计划购买一批桂花树和芒果树.已知桂花树的单价比芒果树的单价多40元,购买3棵桂花树和2棵芒果树共需370元.(1)、桂花树和芒果树的单价各是多少元?(2)、若该村一次性购买这两种树共60棵,且桂花树不少于35棵.设购买桂花树的棵数为n,总费用为w元,求w关于n的函数关系式,并求出该村按怎样的方案购买时,费用最低?最低费用为多少元?22. 如图,直线y=x+1与x轴交于点A,点A关于y轴的对称点为A′,经过点A′和y轴上的点B(0,2)的直线设为y=kx+b.
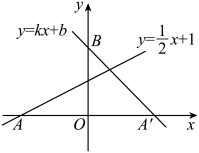 (1)、求点A′的坐标;(2)、确定直线A′B对应的函数表达式.23. 某水果店购进甲、乙两种苹果的进价分别为8元/、12元/ , 这两种苹果的销售额y(单位:元)与销售量x(单位:)之间的关系如图所示.
(1)、求点A′的坐标;(2)、确定直线A′B对应的函数表达式.23. 某水果店购进甲、乙两种苹果的进价分别为8元/、12元/ , 这两种苹果的销售额y(单位:元)与销售量x(单位:)之间的关系如图所示.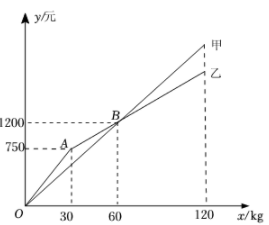 (1)、写出图中点B表示的实际意义;(2)、分别求甲、乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式,并写出x的取值范围;(3)、若不计损耗等因素,当甲、乙两种苹果的销售量均为时,它们的利润和为1500元.求a的值.24. 为落实“双减”政策,丰富课后服务的内容,某学校计划到甲、乙两个体育专卖店购买一批新的体育用品,两个商店的优惠活动如下:
(1)、写出图中点B表示的实际意义;(2)、分别求甲、乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式,并写出x的取值范围;(3)、若不计损耗等因素,当甲、乙两种苹果的销售量均为时,它们的利润和为1500元.求a的值.24. 为落实“双减”政策,丰富课后服务的内容,某学校计划到甲、乙两个体育专卖店购买一批新的体育用品,两个商店的优惠活动如下:甲:所有商品按原价8.5折出售;
乙:一次购买商品总额不超过300元的按原价付费,超过300元的部分打7折.
设需要购买体育用品的原价总额为元,去甲商店购买实付元,去乙商店购买实付元,其函数图象如图所示.
 (1)、分别求 , 关于的函数关系式;(2)、两图象交于点 , 求点坐标;(3)、请根据函数图象,直接写出选择去哪个体育专卖店购买体育用品更合算.25. 在平面直角坐标系中,函数的图象经过点 , , 且与轴交于点 .(1)、求该函数的解析式及点的坐标;(2)、当时,对于的每一个值,函数的值大于函数的值,直接写出的取值范围.26. 定义:对于一次函数 ,我们称函数为函数的“组合函数”.(1)、若m=3,n=1,试判断函数是否为函数的“组合函数”,并说明理由;(2)、设函数与的图象相交于点P.
(1)、分别求 , 关于的函数关系式;(2)、两图象交于点 , 求点坐标;(3)、请根据函数图象,直接写出选择去哪个体育专卖店购买体育用品更合算.25. 在平面直角坐标系中,函数的图象经过点 , , 且与轴交于点 .(1)、求该函数的解析式及点的坐标;(2)、当时,对于的每一个值,函数的值大于函数的值,直接写出的取值范围.26. 定义:对于一次函数 ,我们称函数为函数的“组合函数”.(1)、若m=3,n=1,试判断函数是否为函数的“组合函数”,并说明理由;(2)、设函数与的图象相交于点P.①若 , 点P在函数的“组合函数”图象的上方,求p的取值范围;
②若p≠1,函数的“组合函数”图象经过点P.是否存在大小确定的m值,对于不等于1的任意实数p,都有“组合函数”图象与x轴交点Q的位置不变?若存在,请求出m的值及此时点Q的坐标;若不存在,请说明理由.