浙江省杭州市余杭区、临平区、富阳区等多区2022-2023学年八年级上学期12月月考数学试题
试卷更新日期:2022-12-26 类型:月考试卷
一、选择题:本大题有10个小题,每小题3分,共30分.
-
1. 如果电影院里的5排7座用(5,7)表示,那么7排8座可表示为( )A、(5,7) B、(7,8) C、(8,7) D、(7,5)2. 某辆速度为v(km/h)的车从甲地开往相距s(km)的乙地,全程所用的时间为t(h),在这个变化过程中,( )A、s是变量 B、t是常量 C、v是常量 D、s是常量3. 如果一个三角形的两边长都是6,则第三边的长不能是( )A、3 B、6 C、9 D、134. 平面直角坐标系中,点A(-1,3)到y轴的距离是( )A、1 B、2 C、3 D、45. 已知-2x>4,则下列不等式一定成立的是( )A、x<-2 B、x<2 C、x>-2 D、x>26. 某中学要在校园内划出一块面积是100 m2的矩形土地做花圃,设这个矩形相邻两边长分别为x m和y m,那么y关于x的函数表达式为( )A、y=100x B、y=100-x C、y=50-x D、y=7. 在锐角△ABC中,AB=15,AC=13,BC边上的高AD=12,则BC的长度为( )A、16 B、15 C、14 D、138. 如图,在△ABC中,∠BAC =130°,AB,AC的垂直平分线分别交BC于点E,F,与AB,AC分别交于点D,G,则∠EAF的度数为( )
 A、65° B、60° C、70° D、80°9. 如图是某蓄水池的横断面的示意图,分深水区和浅水区,如果向这个蓄水池中以固定的水流量(单位时间注水的体积)注水(注满水后停止注水),那么下列图中能大致表示水的深度 h 与注水时间 t 之间关系的图象的是( )
A、65° B、60° C、70° D、80°9. 如图是某蓄水池的横断面的示意图,分深水区和浅水区,如果向这个蓄水池中以固定的水流量(单位时间注水的体积)注水(注满水后停止注水),那么下列图中能大致表示水的深度 h 与注水时间 t 之间关系的图象的是( )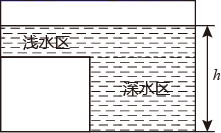 A、
A、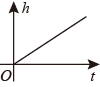 B、
B、 C、
C、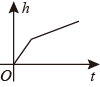 D、
D、 10. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,BE平分∠ABC,CD⊥AB于D,BE与CD相交于F,则CF的长是( )
10. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,BE平分∠ABC,CD⊥AB于D,BE与CD相交于F,则CF的长是( )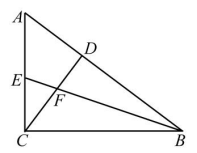 A、1 B、2 C、 D、
A、1 B、2 C、 D、二、填空题:本题有6个小题,每小题4分,共24分.
-
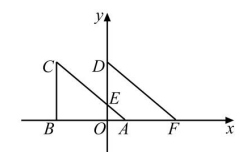
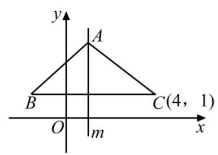
11. “内错角相等,两直线平行”的逆命题是 .12. 到△ABC的三个顶点距离相等的点是△ABC三条线的交点.13. 在平面直角坐标系中,若点P(m+3,3-m)在y轴上,则m的值是.14. 如图,在平面直角坐标系中,△ABC关于直线m对称,直线m与x轴交点为(1,0),点C的坐标为(4,1),则点B的坐标为.
 15. 一次知识竞赛一共有26道题,答对一题得4分、不答得0分,答错一题扣2分,小明有1道题没答,竞赛成绩不少于88分,小明至少答对题.16. 如图,在等腰△ABC中,AB=AC,∠BAC=α, ∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点О重合,则∠CEF的度数是°(用含α的代数式表示).
15. 一次知识竞赛一共有26道题,答对一题得4分、不答得0分,答错一题扣2分,小明有1道题没答,竞赛成绩不少于88分,小明至少答对题.16. 如图,在等腰△ABC中,AB=AC,∠BAC=α, ∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点О重合,则∠CEF的度数是°(用含α的代数式表示).

三、解答题:本题有7小题,共66分.
-
17. 解不等式(组):(1)、2(5x+3)≤x-3(1-2x).(2)、18. 已知正方形网格中每个小正方形的边长为1,按要求作图并计算:

⑴在网格中画出平面直角坐标系,使点A,B的坐标分别为A(2,3),B(3,2),并写出点C的坐标;
⑵作△ABC关于x轴对称的轴对称图形△A1B1C1.
19. 当 x取何正整数值时, 代数式 与 的值的差大于1.20. 已知等腰三角形的周长为12,设腰长为x,底边长为y.(1)、试写出y关于x的函数表达式,并直接写出自变量x的取值范围.(2)、当x=5时,求出函数值.21. 如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且BE=BF. (1)、求证:(2)、若∠CAE=20°,求∠ACF的度数.
(1)、求证:(2)、若∠CAE=20°,求∠ACF的度数.