陕西省咸阳市高新一中2022-2023学年九年级上学期第三次质量检测数学试卷

试卷更新日期：2022-12-26 类型：月考试卷

进入出卷网下载

一、单项选择题（每题3分，共8道小题，共计24分）

1. 若两个三角形相似，且相似比为 1：3 ，则这两个三角形对应角平分线的比为（）

A、 $1 ： \sqrt{3}$ B、1：3 C、1：6 D、1：9

查看试题解析
2. 如图所示的几何体的主视图为（）

A、 B、 C、 D、

查看试题解析
3. 如图，白炽灯下有一个乒乓球，当乒乓球越接近灯泡时，它在地面上的影子（）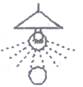

A、越大 B、越小 C、不变 D、无法确定

查看试题解析
4. 李华的弟弟拿着一个菱形木框在阳光下玩耍，李华发现菱形木框在阳光照射下，在地面上形成了各种图形的影子，但以下一种图形始终没有出现，没有出现的图形是（）

A、 B、 C、 D、

查看试题解析
5. 在一张缩印出来的纸上，一个三角形的一条边由原图中的6cm变成了2cm，则缩印出的三角形的面积是原图中三角形面积的（）

A、 $\frac{1}{3}$ B、 $\frac{1}{6}$ C、 $\frac{1}{9}$ D、 $\frac{1}{12}$

查看试题解析
6. 若一个矩形的长和宽是关于 $x$ 的方程 $2 x^{2} - 8 x + m = 0$ 的两根，则该矩形的周长为（）

A、8 B、6 C、4 D、2

查看试题解析
7. 某圆锥的三视图如图所示，由图中数据可知，该圆锥的体积为（）

A、 $12 {π cm}^{3}$ B、 $20 {π cm}^{3}$ C、 $32 {π cm}^{3}$ D、 $48 {π cm}^{3}$

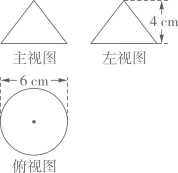查看试题解析
8. 如图，矩形OABC与矩形ODEF是位似图形，点 $A$ 和点 $F$ 分别在 $x$ 轴的正半轴和负半轴上，点 $P$ 是位似中心.若点 $B$ 的坐标为 $(2 ， 3)$ ，点 $E$ 的横坐标为-1，则点 $P$ 的坐标
为（）

A、 $(- 1 ， 0)$ B、 $(- 1.5 ， 0)$ C、 $(- 2 ， 0)$ D、 $(- 2.5 ， 0)$

查看试题解析

二、填空题（每题3分，共5道小题，共计15分）

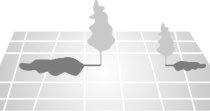
9. 写出一个几何体，使它的三视图都相同.(写出一个即可)

查看试题解析
10. 如图所示是两棵小树在同一时刻的影子，由此推断这是投影.(填“平行”或“中心”)

查看试题解析
11. 在一个不透明的袋子里装有若干个红球和9个黄球，这些球除颜色外都相同，小明每次随机从袋子中摸出一个球，记录下颜色后，放回袋中并摇匀，通过大量重复这样的试验后发现，摸出红球的频率稳定在0.25，则估计袋子中红球的个数是个。

查看试题解析
12. 如图，在平面直角坐标系中，点光源位于 $P (2 ， 2)$ 处，木杆 $A B$ 两端的坐标分别为 $A (0 ， 1) ， B (3 ， 1)$ .则木杆 $A B$ 在 $x$ 轴上的影长CD为

查看试题解析
13. 如图，已知AM和DN分别为 $△ A B C$ 和 $△ D C E$ 的中线， $AM=2DN，B 、 C 、 D$ 在一条直线上， $AB ∥ CD ， AC ∥ DE$ ，若BC=6，则MN的长为

查看试题解析

三、解答题（共13道小题，共计81分）

14. 解方程： ${(x + 3)}^{2} = 5 (x + 3)$ .

查看试题解析
15. 如图，小明和小丽分别站在路灯OA的两侧点 $B$ 和点 $C$ 的位置，已知BD为小明在路灯下的影子，请你画出小丽在路灯下的影子CE.

查看试题解析
16. 如图，已知 $AB ∥ CD$ ，且 $A B = 3 ， C D = 4$ ，连接AC，BD相交于点 $O，OE ⊥ AB$ 于点 $E，OF ⊥ CD$ 于点 $F$ ，求证： $\frac{OE}{OF} = \frac{3}{4}$ .

查看试题解析
17. 如图，在 $△ A B C$ 中，点 $D$ 为边AB的中点，请用尺规作图法在边AC上求作一点 $E$ ，使得 $S_{△ A D E} = \frac{1}{4} S_{△ A B C}$ .(保留作图痕迹，不写作法)

查看试题解析
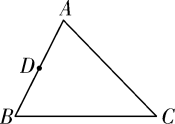18. 蒙古包是内蒙古高原地区的传统民居，如图1是一种蒙古包的大致示意图，若将该蒙古包看成图2所示的，由一个圆柱和一个圆锥组成的几何体，请你画出该几何体的三视图.

查看试题解析
19. 如图，点E，F分别为矩形ABCD的边BC，CD上的点，且 $CE = \frac{2}{3} BC ， CF = \frac{2}{3} CD$ ，若 $△ A B C$ 的周长为39，试求 $△ C E F$ 的周长.

查看试题解析
20. 一个几何体的三视图如图所示(单位： $cm$ )，若其俯视图为正方形，根据图中数据计算这个几何体的体积.

查看试题解析
21. 如图，在平面直角坐标系中， $△$ ABC的顶点坐标分别为：A(1，4)，B(2，2)，C(5，1).

(1)、以原点O为位似中心，在第一象限内画出 $△$ DEF，使得 $△$ DEF与 $△$ ABC位似，且相似比为2：1；

(2)、在(1)的条件下，分别写出点A、B、C的对应点D、E、F的坐标.

查看试题解析
22. 如图，小明与同学合作利用太阳光线测量旗杆的高度，身高1.6m的小明(用图中线段AB表示)落在地面上的影长BC=2.4m.已知 $AB ⊥ BE，DE ⊥ B E ， B ， C ， E$ 在同一水平直线上.

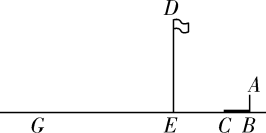(1)、请你在图中画出旗杆DE在同一时刻阳光照射下落在地面上的影子EG；

(2)、若测得此刻旗杆落在地面上的影长EG=16m，请求出旗杆DE的高度.

查看试题解析
23. 家庭成员尤其是父母对待日常生活和T作的态度和处事方法都会对孩子有潜移默化的影响，父母在教育孩子认识问题和解决问题方面对孩子采取怎样的指导、帮助、要求，都会形成孩子对待问题的方式.为此，某校举行了一次“智慧家长”系列讲座活动，活动过程中，甲、乙、丙、丁四位家长踊跃发言，积极互动.活动后校方准备从这四位家长中随机抽选一位作为家长代表做总结发言，并从剩下的三位家长中随机抽选一位做进一步访谈调查.

(1)、选择家长乙作为家长代表做总结发言的概率为

(2)、请用列表法或画树状图的方法求家长甲作为家长代表做总结发言，且家长丁被抽选做进—步访谈调查的概率.

查看试题解析
24. 如图，在 $△ A B C$ 中， $∠ BAC = 90^{\circ} ， D$ 是BC的中点，过点 $A$ 作 $AE ∥ BC$ ，且 $A E = B D$ ，连接AD、CE

(1)、求证：四边形ADCE是菱形；

(2)、若AC=6，AB=8，求菱形ADCE的面积.

查看试题解析
25. 学习了投影和相似的知识后，王志和他的朋友们来到操场，想测量操场边路灯的高度 $P G$ ，如图，操场边的路灯照在水平放置的单杠AB上，在地面上留下影子CD，经测量得知AB=1.8米，CD=3.24米，单杠高 $1.6$ 米(即AE=BF=1.6米).已知 $PG ⊥ DG，AE ⊥ D G ， B F ⊥ D G$ ，点C、D、E、F、G在同一水平直线上.请你求出路灯的高度PG.

查看试题解析
26. 如图，在正方形ABCD中，E、F分別是线段AD、AB上的点(不与端点重合)，连接 $BE，AP ⊥ BE$ 于点 $P$ ，连接PF.

(1)、如图1，如果点 $F$ 是AB的中点，求证： $BP \cdot BE=2PF \cdot BC$ .

(2)、如图2，如果AE=AF，连接CP：
①求证： $CP ⊥ FP$ ；

②当 $\frac{AE}{AB} = \frac{2}{3}$ ，且 $△ P A F$ 的面积为4时，求 $△ P B C$ 的面积.

查看试题解析