贵州省黔南布依族苗族自治州长顺县教育局教研室2022-2023学年八年级上学期期中数学试题

试卷更新日期：2022-12-26 类型：期中考试

进入出卷网下载

一、单选题

1. 第24届冬季奥林匹克运动会于2022年2月20日在世界首个“双奥之城”-北京圆满落下帷幕.下面由北京冬奥会比赛项目图标组成的四个图形中，可看作轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知 $△ A B C$ 中， $A B = 5$ ， $B C = 4$ ，则 $A C$ 长度的取值范围是（）

A、 $1 < A C < 9$ B、 $1 \leq A C < 9$ C、 $1 < A C \leq 9$ D、 $1 \leq A C \leq 9$

查看试题解析
3. 如图，把 $△ A B C$ 沿EF翻折，叠合后的图形如图，若 $∠ A = 60 °$ ， $∠ 1 = 95 °$ ，则 $∠ 2$ 的度数是（）

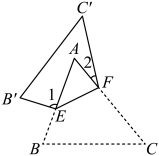A、15° B、20° C、25° D、35°

查看试题解析
4. 为了求n边形内角和，下面是老师与同学们从n边形的个顶点引出的对角线把n边形划分为若干个三角形，然后得出n边形的内角和公式．这种数学的推理方式是（）

A、归纳推理 B、数形结合 C、公理化 D、演绎推理

查看试题解析
5. 小聪利用最近学习的数学知识，给同伴出了这样一道题：假如从点A出发，沿直线走6米后向左转 $θ$ ，接着沿直线前进6米后，再向左转 $θ$ ……如此下去，当他第一次回到A点时，发现自己走了72米， $θ$ 的度数为（）

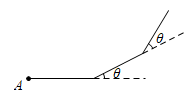A、30° B、36° C、60° D、72°

查看试题解析
6. 若等腰三角形有一个角等于50°，则这个等腰三角形的顶角的度数是（）

A、50° B、80° C、65°或50° D、50°或80°

查看试题解析
7. 下列条件，不能判定两个直角三角形全等的是（）

A、两个锐角对应相等 B、一个锐角和斜边对应相等 C、两条直角边对应相等 D、一条直角边和斜边对应相等

查看试题解析
8. 下列说法错误的是（）

A、直角三角形的两个锐角互为余角 B、 $△ A B C ≌ △ D E F$ ，则 $△ A B C$ 与 $△ D E F$ 一定关于某条直线对称 C、连接轴对称图形的对应点的线段必被对称轴垂直平分 D、 $(n + 1)$ 边形的内角和比 $n$ 边形的内角和大180°

查看试题解析
9. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ 于点 $D$ ， $B E ⊥ A C$ 与点 $E$ ， $B E$ 与 $A D$ 交于点 $F$ ，若 $A D = B D = 5$ ， $C D = 3$ ，则 $A F$ 的长为（）

A、3 B、3.5 C、2.5 D、2

查看试题解析
10. 如图， $△ A B C$ 的三边 $A B$ 、 $B C$ 、 $C A$ 长分别是30、40、50， $∠ A B C$ 和 $∠ A C B$ 的角平分线交于O，则 $S_{△ A B O} ： S_{△ B C O} ： S_{△ C A O}$ 等于（）

A、 $1 ： 1 ： 1$ B、 $1 ： 2 ： 3$ C、 $2 ： 3 ： 4$ D、 $3 ： 4 ： 5$

查看试题解析
11. 如图， $△ A B C$ 中， $A B$ 的垂直平分线交 $A C$ 与点 $M ．$ 若 $A C = 9 c m$ ， $B C = 5 c m$ ，则 $△ M B C$ 的周长是（） $c m$ .

A、23 B、19 C、14 D、12

查看试题解析
12. 如图，已知∠MON=30°，点A₁ ， A₂ ， A₃ ， …在射线ON上，点B₁ ， B₂ ， B₃ ， …在射线OM上，△A₁B₁A₂ ， △A₂B₂A₃ ， △A₃B₃A₄ ， …均为等边三角形，若OA₁=2，则△A₅B₅A₆的边长为（）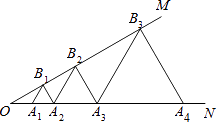

A、8 B、16 C、24 D、32

查看试题解析

二、填空题

13. 点 $A (a ， 1)$ 和点 $B (- 1 ， b)$ 关于 $x$ 轴对称，则 $a + b =$ .

查看试题解析
14. 正八边形一个外角的大小为度.

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ A B C$ 和 $∠ A C B$ 的平分线交于点 $D$ ，过点 $D$ 作 $E F ∥ B C$ 交 $A B$ 于点 $E$ ，交 $A C$ 于点 $F$ ，若 $A B = 10$ ， $B C = 7$ ， $A C = 8$ ，则 $△ A E F$ 的周长为.

查看试题解析
16. 如图，在等腰三角形 $A B C$ 中， $A B = A C$ ， $D E$ 垂直平分 $A B$ ，交 $A B$ 于点 $E$ ，交 $A C$ 于点 $D$ .若 $∠ A D E = 40 °$ ，则 $∠ C B D =$ $°$ .

查看试题解析

三、解答题

17. 在△ABC中，BC＝8，AB＝1；

(1)、若AC是整数，求AC的长；

(2)、已知BD是△ABC的中线，若△ABD的周长为10，求△BCD的周长．

查看试题解析
18. 如图， $C E$ 是 $△ A B C$ 的外角 $∠ A C D$ 的平分线，且 $C E$ 交 $B A$ 的延长线于点E.

(1)、若 $∠ B = 35 °$ ， $∠ E = 25 °$ ，求 $∠ C A E$ 的度数；

(2)、证明： $∠ B A C = ∠ B + 2 ∠ E$ .

查看试题解析
19. 已知一个正多边形的内角和比外角和的3倍多 $180 °$ ，求这个正多边形的边数和每个内角的度数.

查看试题解析
20. 已知 $△ A B C$ 在平面直角坐标系中的位置如图所示，点 $A$ ， $B$ ， $C$ 均在格点（小正方形的顶点）上.
⑴作出 $△ A B C$ 关于 $x$ 轴对称的 $△ A_{1} B_{1} C_{1}$ ；
⑵作出 $△ A B C$ 向右平移5个单位长度后的 $△ A_{2} B_{2} C_{2}$ .

查看试题解析
21. 如图所示，已知CD＝BD，点E、F分别是CD、BD的中点，∠CAF＝∠BAE，∠B＝∠C.求证：AE＝AF.

查看试题解析
22. 【概念认识】
如图①，在 $∠ A B C$ 中，若 $∠ A B D = ∠ D B E = ∠ E B C$ ，则 $B D$ ， $B E$ 叫做 $∠ A B C$ 的“三分线”，其中 $B D$ 是“邻 $B A$ 三分线” $B E$ 是“邻 $B C$ 三分线”．
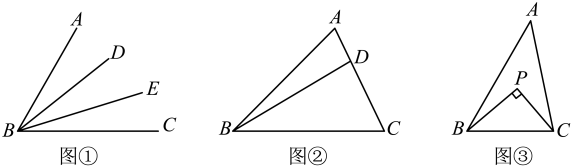
【问题解决】

(1)、如图②，在 $△ A B C$ 中， $∠ A = 70 °$ ， $∠ A B C = 45 °$ ，若 $∠ A B C$ 的邻 $B A$ 三分线 $B D$ 交 $A C$ 于点D，则 $∠ B D C$ 的度数为；

(2)、如图③，在 $△ A B C$ 中， $B P$ ， $C P$ 分别是 $∠ A B C$ 邻 $B A$ 三分线和 $∠ A C B$ 邻 $C A$ 三分线，且 $B P ⊥ P C$ ，求 $∠ A$ 度数．

查看试题解析
23. 如图，在 $△ A B C$ 中， $A B = A C$ ，过点 $A$ 作 $A D ⊥ B C$ 于点 $D$ ，过点 $B$ 作 $B E ⊥ A C$ 于点 $E$ ， $A D$ 与 $B E$ 交于点 $F$ ，连接 $C F$ .

(1)、求证： $∠ A B F = ∠ A C F$ ；

(2)、若 $∠ B A C = 48 °$ ，求 $∠ C F E$ 的度数.

查看试题解析
24. 综合与实践
如图， $△ A B C$ 是等边三角形， $D$ ， $E$ 分别是 $A B$ ， $A C$ 的中点，连接 $D E$ .

(1)、求证： $D E ∥ B C$ ；

(2)、在线段 $D E$ 的延长线上取点 $F$ ， $G$ ，使 $F G = D E$ ，直线 $A F$ ， $C G$ 交于点 $H$ .求证： $△ A D F ≌ △ C E G$ .

查看试题解析
25. 综合与探究
【问题情境】

在 $△ A B C$ 中， $A B = A C$ ，点 $D$ 是直线 $B C$ 上一点，连接 $A D$ ，以 $A D$ 为边向右作 $△ A D E$ ，使得 $A D = A E$ ， $∠ D A E = ∠ B A C$ ，连接 $C E$ .

(1)、如图1，当点 $D$ 在 $B C$ 边上时，
①若 $∠ B A C = 40 °$ ，则 $∠ D C E =$ ▲ °；
②观察以上结果，猜想 $∠ B A C$ 与 $∠ D C E$ 的数量关系，并说明理由.

(2)、【拓展应用】
如图2，当点 $D$ 在 $B C$ 的延长线上时，请判断 $∠ B A C$ 与 $∠ D C E$ 的数量关系，并说明理由.

查看试题解析