贵州省黔南布依族苗族自治州长顺县2022-2023学年九年级上学期教学质量评估(二)数学试题
试卷更新日期:2022-12-26 类型:期中考试
一、单选题
-
1. 下列方程一定是一元二次方程的是( )A、3x2+﹣1=0 B、5x2﹣6y﹣3=0 C、ax2﹣x+2=0 D、3x2﹣2x﹣1=02. 下列关于防范“新冠肺炎”的标志中既是轴对称图形,又是中心对称图形的是( )A、
 戴口罩讲卫生
B、
戴口罩讲卫生
B、 勤洗手勤通风
C、
勤洗手勤通风
C、 有症状早就医
D、
有症状早就医
D、 少出门少聚集
3. 抛物线y=x2﹣9的顶点坐标是( )A、(0,﹣9) B、(﹣3,0) C、(﹣9,0) D、(3,0)4. 若 , 是方程的一个根,则值满足( )A、 B、 C、 D、5. 等腰三角形的两边的长是方程两个根,则此三角形的周长是( )A、7 B、8 C、7或8 D、以上都不对6. 不论x,y取何值,代数式的值( )A、总不小于-3 B、总不大于-3 C、总大于2 D、总小于27. 若一元二次方程的两根为和 , 则的值等于( )A、1 B、 C、 D、8. 将抛物线向左平移1个单位长度,得到的抛物线是( )A、 B、 C、 D、9. 如图所示,如图可以看作是一个菱形通过几次旋转得到的,每次可能旋转( )
少出门少聚集
3. 抛物线y=x2﹣9的顶点坐标是( )A、(0,﹣9) B、(﹣3,0) C、(﹣9,0) D、(3,0)4. 若 , 是方程的一个根,则值满足( )A、 B、 C、 D、5. 等腰三角形的两边的长是方程两个根,则此三角形的周长是( )A、7 B、8 C、7或8 D、以上都不对6. 不论x,y取何值,代数式的值( )A、总不小于-3 B、总不大于-3 C、总大于2 D、总小于27. 若一元二次方程的两根为和 , 则的值等于( )A、1 B、 C、 D、8. 将抛物线向左平移1个单位长度,得到的抛物线是( )A、 B、 C、 D、9. 如图所示,如图可以看作是一个菱形通过几次旋转得到的,每次可能旋转( ) A、 B、 C、 D、10. 在同一平面直角坐标系中,一次函数y=ax+b和二次函数y=ax2+bx+c的图象可能为( )A、
A、 B、 C、 D、10. 在同一平面直角坐标系中,一次函数y=ax+b和二次函数y=ax2+bx+c的图象可能为( )A、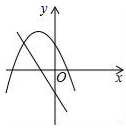 B、
B、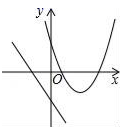 C、
C、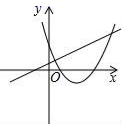 D、
D、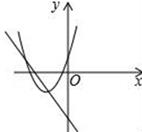 11. 某县为发展教育事业,加强了对教育经费的投入,2020年投入3000万元,预计2022年投入5000万元.设教育经费的年平均增长率为x,根据题意,下面所列方程正确的是( )A、 B、 C、 D、12. 二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,下列结论:①abc>0;②a+c﹣b>0;③3a+c>0;④a+b≤m(am+b)(m为实数).其中结论正确的个数为( )
11. 某县为发展教育事业,加强了对教育经费的投入,2020年投入3000万元,预计2022年投入5000万元.设教育经费的年平均增长率为x,根据题意,下面所列方程正确的是( )A、 B、 C、 D、12. 二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,下列结论:①abc>0;②a+c﹣b>0;③3a+c>0;④a+b≤m(am+b)(m为实数).其中结论正确的个数为( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 方程3x(x-1)=6(x-1)的根为.14. 抛物线过 , , 三点,则 , , 的大小关系是.15. 如图, 是等边三角形, 为 边上的点, 经旋转后到达 的位置,若 ,那么 .
 16. 如图,二次函数y=a(x﹣2)2+k(a>0)的图象过原点,与x轴正半轴交于点A,矩形OABC的顶点C的坐标为(0,﹣2),点P为x轴上任意一点,连结PB、PC.则△PBC的面积为 .
16. 如图,二次函数y=a(x﹣2)2+k(a>0)的图象过原点,与x轴正半轴交于点A,矩形OABC的顶点C的坐标为(0,﹣2),点P为x轴上任意一点,连结PB、PC.则△PBC的面积为 .
三、解答题
-
17. 按题目要求解答问题.(1)、用适当的方法解方程:;(2)、已知x是方程的根,求代数式的值.18. 若关于x的方程mx2-2x+3=0有两个实数根.(1)、求m的取值范围;(2)、方程有两个相等的实数根时,求出方程的根.19. 阅读下面的例题,
范例:解方程 ,
解:(1)当 时,原方程化为 , 解得: , (不合题意,舍去).
(2)当x<0时,原方程化为 , 解得: , (不合题意,舍去).∴原方程的根是 , , 请参照例题解方程
20. 如图,一个10×10网格,每个小正方形的边长均为1,每个小正方形的顶点叫格点,△ABC的顶点均在格点上.
⑴画出△ABC关于直线l的对称的△A1B1C1.
⑵画出△ABC关于点P的中心对称图形△A2B2C2.
⑶△AA1B1C1与△A2B2C2组成的图形 ▲ (是或否)轴对称图形,如果是轴对称图形,请画出对称轴.
21. 某扶贫单位为了提高贫困户的经济收入,购买了的铁栅栏,准备用这些铁栅栏为贫困户靠墙(墙长)围建一个矩形鸡舍,门宽 , 如图所示. (1)、若要建的矩形鸡舍面积为 , 求的长;(2)、该鸡舍的最大面积可以达到.22. 如图,在中, , 将绕点顺时针方向旋转得到点在上,再将沿着所在直线翻转得到 , 连接.
(1)、若要建的矩形鸡舍面积为 , 求的长;(2)、该鸡舍的最大面积可以达到.22. 如图,在中, , 将绕点顺时针方向旋转得到点在上,再将沿着所在直线翻转得到 , 连接. (1)、求证:四边形是菱形;(2)、连接并延长交于连接请问:四边形是什么特殊四边形?为什么?23. 如图,抛物线(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C,连接BC,与抛物线的对称轴交于点E,顶点为点D.
(1)、求证:四边形是菱形;(2)、连接并延长交于连接请问:四边形是什么特殊四边形?为什么?23. 如图,抛物线(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C,连接BC,与抛物线的对称轴交于点E,顶点为点D. (1)、求抛物线的解析式;(2)、求△BOC的面积.24. 中考前,某校文具店以每套5元购进若干套考试用具,为让利考生,该店决定售价不超过7元,在几天的销售中发现每天的销售数量y(套)和售价x(元)之间存在一次函数关系,绘制图象如图.
(1)、求抛物线的解析式;(2)、求△BOC的面积.24. 中考前,某校文具店以每套5元购进若干套考试用具,为让利考生,该店决定售价不超过7元,在几天的销售中发现每天的销售数量y(套)和售价x(元)之间存在一次函数关系,绘制图象如图. (1)、y与x的函数关系式为(并写出x的取值范围);(2)、若该文具店每天要获得利润80元,则该套文具的售价为多少元?(3)、设销售该套文具每天获利w元,则销售单价应为多少元时,才能使文具店每天的获利最大?最大利润是多少?25. 在平面直角坐标系中,二次函数 y=ax2+bx+2 的图象与 x 轴交于 A(﹣3,0),B(1,0)两点,与 y 轴交于点C.
(1)、y与x的函数关系式为(并写出x的取值范围);(2)、若该文具店每天要获得利润80元,则该套文具的售价为多少元?(3)、设销售该套文具每天获利w元,则销售单价应为多少元时,才能使文具店每天的获利最大?最大利润是多少?25. 在平面直角坐标系中,二次函数 y=ax2+bx+2 的图象与 x 轴交于 A(﹣3,0),B(1,0)两点,与 y 轴交于点C. (1)、求这个二次函数的关系解析式 ,x 满足什么值时 y﹤0 ?(2)、点 p 是直线 AC 上方的抛物线上一动点,是否存在点 P , 使△ACP 面积最大?若存在,求出点 P的坐标;若不存在,说明理由(3)、点 M 为抛物线上一动点,在 x 轴上是否存在点 Q , 使以 A、C、M、Q 为顶点的四边形是平行四边形?若存在,直接写出点 Q 的坐标;若不存在,说明理由.
(1)、求这个二次函数的关系解析式 ,x 满足什么值时 y﹤0 ?(2)、点 p 是直线 AC 上方的抛物线上一动点,是否存在点 P , 使△ACP 面积最大?若存在,求出点 P的坐标;若不存在,说明理由(3)、点 M 为抛物线上一动点,在 x 轴上是否存在点 Q , 使以 A、C、M、Q 为顶点的四边形是平行四边形?若存在,直接写出点 Q 的坐标;若不存在,说明理由.