贵州省黔南布依族苗族自治州惠水县2022-2023学年九年级上学期期中数学试题

试卷更新日期：2022-12-26 类型：期中考试

进入出卷网下载

一、单选题

1. 2022贵阳国际车展以“潮黔看 $\cdot$ 驭未来”为主题，汇聚80余个汽车品牌，为市民带来更炫酷、更极致的观展体验.下面是此次车展中的几个车标，其中是中心对称图形而不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列方程中，是一元二次方程的是（）

A、 $x^{2} - y^{2} - 3 = 0$ B、 $\frac{1}{5} x^{2} - x - 3 = 0$ C、 $a x^{2} - y - 3 = 0$ D、 $x^{2} - y - 3 = 0$

查看试题解析
3. 若方程 $\frac{1}{2} x^{2} = 17 - 3 x$ 化成一般形式后，二次项的系数为 $\frac{1}{2}$ ，则它的一次项是（）

A、-3 B、3 C、-3x D、3x

查看试题解析
4. 如图，在以下平面直角坐标系中， $△ A B C$ 绕某点旋转90°得到 $△ A^{'} B^{'} C^{'}$ ，则旋转中心是点（） .

A、O B、M C、N D、无法确定

查看试题解析
5. 一元二次方程 $x^{2} - 5 x - 6 = 0$ ，下列分解正确的是（）

A、 $(x + 1) (x - 6) = 0$ B、 $(x - 1) (x + 6) = 0$ C、 $(x - 2) (x + 3) = 0$ D、 $(x + 2) (x - 3) = 0$

查看试题解析
6. 已知关于x的一元二次方程ax²﹣4x﹣2＝0有实数根，则a的取值范围是（）

A、a≥﹣2 B、a＞﹣2 C、a≥﹣2且a≠0 D、a＞﹣2且a≠0

查看试题解析
7. 已知点A是抛物线 $y = x^{2} - 8 x + 13$ 图象的顶点，点A和点 $B$ 关于原点成中心对称，则点 $B$ 的坐标是（）

A、 $(4 ， 3)$ B、 $(- 4 ， 3)$ C、 $(- 4 ， - 3)$ D、 $(- 3 ， 4)$

查看试题解析
8. 在同一平面直角坐标系中，一次函数 $y = a x + b$ 与二次函数 $y = b (x - a)^{2}$ 的图象大致为（）

A、 B、 C、 D、

查看试题解析
9. 已知二次函数 $y = - (x - 1)^{2} + 2$ ，当 $t < x < 5$ 时. $y$ 随 $x$ 的增大而减小，则实数 $t$ 的取值范围是（）

A、 $0 < t \leq 1$ B、 $t \geq 1$ C、 $1 \leq t < 5$ D、 $t \geq 5$

查看试题解析
10. 春季，某种流行性感冒病菌传播非常快，如果一个人被感染，经过两轮传染后就会有81人被感染，若设每轮传染中平均每人可以传染x人，则根据题意，可列方程为（）

A、 $x^{2} = 81$ B、 $x + x^{2} = 81$ C、x（1+x）＝81 D、 ${(1 + x)}^{2} = 81$

查看试题解析
11. 直角三角形两直角边是方程 $x^{2} - 8 x + 14 = 0$ 的两根，则它的斜边为（）

A、8 B、7 C、6 D、 $2 \sqrt{7}$

查看试题解析
12. 如图，抛物线 $y = a x^{2} + b x + c$ 与 $x$ 轴正半轴交于 $A$ ， $B$ 两点，若点 $A$ 坐标为 $(1 ， 0)$ ，点 $B$ 坐标为 $(5 ， 0)$ ，有下列结论：
① $a b c < 0$ ；② $2 a + b > 0$ ；③ $a + 4 c < 0$ ；④当 $0 \leq x \leq 4$ 时， $c \leq y \leq 16 a + 4 b + c$ .
其中结论正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 如图，将右边的图案变成左边的图案，是通过变化得到的.

查看试题解析
14. 若点A（-2，y₁）和B（1，y₂）是二次函数 $y ＝ - x^{2} - k$ 图象上的两点，则y₁y₂（填“＜”“＝”或“＞”）.

查看试题解析
15. 《九章算术》是我国古代数学的经典著作，它的出现标志着中国古代数学形成了完整的体系，其“勾股”章中记载了一个数学问题：“今有户高多于广六尺，两隅相去适一丈，问户高、广各几何？”译文为：“已知有一扇矩形门的高比宽多6尺，门的对角线长为1丈（1丈＝10尺），那么门的高和宽各是多少？”如果设门的宽为x尺，则可列方程为．

查看试题解析
16. 对于实数p，q，我们用符号max{p，q}表示p，q两数中较大的数，如max{2，3}＝3，若 $m a x {(x - 1)^{2} ， x^{2}}$ ＝1，则x＝.

查看试题解析

三、解答题

17.

(1)、如图所示分别是二次函数 $y = a x^{2} + b x + c$ 与 $y = a^{'} x^{2} + b^{'} x + c^{'}$ 的图象.用“ $<$ ”或“ $>$ ”填空： $a$ $a^{'}$ ， $c$ $c^{'}$ .

(2)、在本学期我们已经学习了一元二次方程的三种解法，他们分别是配方法、公式法和因式分解法，请从下列一元二次方程中任选两个，并解这两个方程.
① $(x - 3)^{2} = 5 (3 - x)$ ；
② $(2 x - 1)^{2} - 9 = 0$ ；
③ $2 x^{2} - \sqrt{3} x - 3 = 0$ ；
④ $x^{2} - 2 x - 15 = 0$ .

查看试题解析
18. 如图：在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度；已知△ABC.

（1）作出△ABC关于x轴对称的△A₁B₁C₁ ，（只画出图形）.

（2）作出△ABC关于原点O成中心对称的△A₂B₂C₂ ，（只画出图形），写出B₂和C₂的坐标.

查看试题解析
19. 关于 $x$ 的一元二次方程 $x^{2} - (m - 1) x + (m - 2) = 0$ .

(1)、求证：无论 $m$ 取何值，方程总有实数根；

(2)、已知方程有一根大于6，求 $m$ 的取值范围.

查看试题解析
20. 如图，某校新生军训摄影作品[七寸照片(长7英寸，宽5英寸)]，现将照片贴在一张矩形衬纸的正中央，照片四周外露村纸的宽度相同；矩形衬纸的面积与照片的面积之比为9： 5，求照片四周外露衬纸的宽度.

查看试题解析
21. 我们将平面直角坐标系 $x O y$ 中的图形D和点P给出如下定义：如果将图形D绕点P顺时针旋转90°得到图形 $D'$ ，那么图形 $D'$ 称为图形D关于点P的“垂直图形”．已知点A的坐标为 $(- 2 ， 1)$ ，点B的坐标为（0，1）， $△ A B O$ 关于原点O的“垂直图形”记为 $△ A' B' O'$ ，点A、B的对应点分别为点 $A' ， B'$ ．

(1)、请写出：点 $A'$ 的坐标为；点 $B'$ 的坐标为；

(2)、请求出经过点A、B、 $B'$ 的二次函数解析式；

(3)、请直接写出经过点A、B、 $A'$ 的抛物线的表达式为．

查看试题解析
22. 芯片目前是全球紧缺资源，市政府通过资本招商引进“芯屏汽合、集终生智”等优势产业，发展新兴产业.某芯片公司，引进了一条内存芯片生产线，开工第一季度生产200万个，第三季度生产288万个.试回答下列问题：

(1)、已知每季度生产量的平均增长率相等，求前三季度生产量的平均增长率；

(2)、经调查发现，1条生产线最大产能是600万个/季度，若每增加1条生产线，每条生产线的最大产能将减少20万个/季度.现该公司要保证每季度生产内存芯片2600万个，在增加产能同时又要节省投入成本的条件下（生产线越多，投入成本越大），应该再增加几条生产线？

查看试题解析
23. 如图， $R t △ A B C$ 中， $∠ C = 90 °$ ， $B C = a$ ， $A C = b (a < b)$ ， $A B = 5$ ， $a$ ， $b$ 是方程 $x^{2} - (m - 1) x + (m + 4) = 0$ 的两根.

(1)、求 $a$ ， $b$ ；

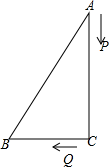(2)、 $P$ ， $Q$ 两点分别从 $A$ ， $C$ 出发，分别以每秒2个单位，1个单位的速度沿边 $A C$ ， $B C$ 向终点 $C$ ， $B$ 运动，（有一个点达到终点则停止运动），求经过多长时间后 $P Q = 2$ ？

查看试题解析
24. 如图，在平面直角坐标系中，矩形 $O A B C$ 的顶点 $A (0 ， 3)$ ， $C (- 1 ， 0) .$ 将矩形 $O A B C$ 绕原点顺时针旋转 $90 °$ ，得到矩形 $O A^{'} B^{'} C^{'}$ ，设直线 $B B^{'}$ 与 $x$ 轴交于点 $M$ 、与 $y$ 轴交于点 $N$ ，抛物线 $y = a x^{2} + 2 x + c$ 的图象经过点 $C$ 、 $M$ 、 $N$ .

(1)、点 $B$ 的坐标为，点 $B^{'}$ 的坐标为；

(2)、求抛物线的解析式；

(3)、求 $△ C M N$ 的面积.

查看试题解析
25. 九年级数学兴趣小组在课外学习时遇到这样一个问题：
定义：如果二次函数 $y = a_{1} x^{2} + b_{1} x + c_{1}$ （ $a_{1} \neq 0 ， a_{1} ， b_{1} ， c_{1}$ 是常数）与 $y = a_{2} x^{2} + b_{2} x + c_{2}$ （ $a_{2} \neq 0 ， a_{2} ， b_{2} ， c_{2}$ 是常数）满足 $a_{1} + a_{2} = 0$ ， $b_{1} = b_{2}$ ， $c_{1} + c_{2} = 0$ ，则这两个函数互为“旋转函数” $.$ 求函数 $y = 2 x^{2} - 3 x + 1$ 的“旋转函数”.
小组同学是这样思考的，由函数 $y = 2 x^{2} - 3 x + 1$ 可知， $a_{1} = 2$ ， $b_{1} = - 3$ ， $c_{1} = 1$ ，根据 $a_{1} + a_{2} = 0$ ， $b_{1} = b_{2}$ ， $c_{1} + c_{2} = 0$ ，求出 $a_{2}$ ， $b_{2}$ ， $c_{2}$ 就能确定这个函数的“旋转函数”.
请参照小组同学的方法解决下面问题：

(1)、函数 $y = x^{2} - 4 x + 3$ 的“旋转函数”是；

(2)、若函数 $y = 5 x^{2} + (m - 1) x + n$ 与 $y = - 5 x^{2} - n x - 3$ 互为“旋转函数”，求 $(m + n)^{2022}$ 的值；

(3)、已知函数 $y = 2 (x - 1) (x + 3)$ 的图像与 $x$ 轴交于 $A$ ， $B$ 两点，与 $y$ 轴交于点 $C$ ，点 $A$ ， $B$ ， $C$ 关于原点的对称点分别是 $A_{1}$ ， $B_{1}$ ， $C_{1}$ ，试求证：经过点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的二次函数与 $y = 2 (x - 1) (x + 3)$ 互为“旋转函数”.

查看试题解析