贵州省黔东南苗族侗族自治州岑巩县教育和科技局教研室2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-12-26 类型：期中考试

进入出卷网下载

一、单选题

1. 方程 $x^{2} = x$ 的解为（）

A、 $x = - 1$ B、x＝0 C、x＝1 D、 $x_{1} = 0$ ， $x_{2} = 1$

查看试题解析
2. 下列函数中，y关于x的二次函数的是（）

A、y＝x³＋2x²＋3 B、y＝- $\frac{1}{x^{2}}$ C、y＝x²＋x D、y＝mx²＋x＋1

查看试题解析
3. 抛物线 $y = {(x - 1)}^{2} + 2$ 的顶点坐标是（）

A、（﹣1，2） B、（﹣1，﹣2） C、（1，﹣2） D、（1，2）

查看试题解析
4. 把抛物线 $y = x^{2} + 1$ 向右平移3个单位，再向下平移2个单位，得到抛物线（）

A、 $y = {(x + 3)}^{2} - 1$ B、 $y = (x + 3)^{2} + 3$ C、 $y = (x - 3)^{2} - 1$ D、 $y = (x - 3)^{2} + 3$

查看试题解析
5. 用配方法解一元二次方程 $x^{2} - 4 x - 1 = 0$ 时，变形正确的是（）

A、 ${(x + 2)}^{2} = 3$ B、 ${(x + 2)}^{2} = 5$ C、 ${(x - 2)}^{2} = 3$ D、 ${(x - 2)}^{2} = 5$

查看试题解析
6. 关于x的一元二次方程 $x^{2} - m x + (m - 2) = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
7. 某省加快新旧动能转换，促进企业创新发展．某企业一月份的营业额是1000万元，月平均增长率相同，第一季度的总营业额是3990万元．若设月平均增长率是x，那么可列出的方程是（）

A、1000（1+x）²＝3990 B、1000+1000（1+x）+1000（1+x）²＝3990 C、1000（1+2x）＝3990 D、1000+1000（1+x）+1000（1+2x）＝3990

查看试题解析
8. 下列图像中，当 $a b > 0$ 时，函数 $y = a x^{2}$ 与 $y = a x + b$ 的图像是（）

A、 B、 C、 D、

查看试题解析
9. 若 $A (\frac{3}{4} ， y_{1})$ ， $B (- \frac{5}{4} ， y_{2})$ ， $C (\frac{1}{4} ， y_{3})$ 为二次函数 $y = x^{2} + 4 x - 5$ 的图象上的三点，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{3} < y_{2} < y_{1}$ C、 $y_{2} < y_{3} < y_{1}$ D、 $y_{1} < y_{3} < y_{2}$

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，它与x轴的两个交点分别为 $(- 1 ， 0)$ ， $(3 ， 0)$ .对于下列命题：① $b + 2 a = 0$ ；② $a b c < 0$ ；③ $a - 2 b + 4 c < 0$ ；④ $8 a + c < 0$ ；⑤ $a + b + c > 0$ .其中正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 若关于 $x$ 的方程 $(m - 1) x^{2} + m x - 1 = 0$ 是一元二次方程，则 $m$ 的取值范围是.

查看试题解析
12. 二次函数 $y = x^{2} - 2 x + 1$ 与x轴的交点个数是.

查看试题解析
13. 抛物线y＝2x²-4x+4的顶点坐标为.

查看试题解析
14. 若关于x的一元二次方程 $x^{2} + m x - 6 = 0$ 的一个根是2，则另一个根为.

查看试题解析
15. 已知关于x的方程x²+x﹣m＝0有实数解，则m的取值范围是.

查看试题解析
16. 以2和 $- 3$ 为根的一元二次方程为.（写出一个即可）

查看试题解析
17. 二次函数y＝ax²+bx+c（a≠0）的部分图象如图所示，对称轴为直线x＝-1，则关于x的方程ax²+bx+c＝0（a≠0）的解为.

查看试题解析
18. 已知方程 $x^{2} + 2021 x - 2 = 0$ 的两根分别为 $α$ 和 $β$ ，则代数式 $α^{2} + α β + 2021 α$ 的值为.

查看试题解析

三、解答题

19. 按要求解方程.

(1)、 $x^{2} - 6 x - 5 = 4$ （配方法）

(2)、 $2 x^{2} - 2 \sqrt{2} x + 1 = 0$ （公式法）

查看试题解析
20. 用合适的方法解方程.

(1)、 $x (x + 4) = 8 x + 12$

(2)、 $1 - 8 x + 16 x^{2} = 2 - 8 x$

查看试题解析
21. 如图，在 $R t △ O A B$ 中， $∠ O A B = 90 °$ ，且点 $B$ 的坐标为 $(4 ， 2)$ .
⑴画出 $△ O A B$ 向下平移3个单位后的 $△ O_{1} A_{1} B_{1}$ ；并写出对应点的坐标；
⑵画出 $△ O A B$ 绕点 $O$ 逆时针旋转 $90 °$ 后的 $△ O A_{2} B_{2}$ ，并写 $A_{2}$ 与 $B_{2}$ 的坐标.

查看试题解析
22. 已知二次函数y=﹣x²+2x+m．

(1)、如果二次函数的图象与x轴有两个交点，求m的取值范围；

(2)、如图，二次函数的图象过点A（3，0），与y轴交于点B，直线AB与这个二次函数图象的对称轴交于点P，求点P的坐标．

(3)、根据图象直接写出使一次函数值大于二次函数值的x的取值范围．

查看试题解析
23. 如下图所示，在宽为20m，长为32m的矩形耕地上，修筑同样宽的三条道路（互相垂直），把耕地分成大小不等的六块试验田，要使试验田的面积为 $570 m^{2}$ ，道路应为多宽？

查看试题解析
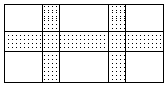24. 如图所示，有一个抛物线形的拱形桥洞，桥洞离水面的最大高度AB为4m，跨度OC为10m.

(1)、请建立适当直角坐标系，并求这条抛物线所对应的函数关系式.

(2)、如图，在AB右边1m的D处所对应桥洞离水面的高是多少？

查看试题解析
25. 为满足市场需求，某超市在五月初五“端午节”来临前夕，购进一种品牌粽子，每盒进价是40元，超市规定每盒售价不得少于45元．根据以往销售经验发现：当售价定为每盒45元时，每天可卖出700盒，每盒售价每提高1元，每天要少卖出20盒．

(1)、试求出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；

(2)、当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？

查看试题解析
26. 如图，抛物线y=x²+bx+c与x轴交于A（﹣1，0），B（3，0）两点．

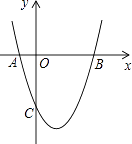(1)、求该抛物线的解析式；

(2)、求该抛物线的对称轴以及顶点坐标；

(3)、设（1）中的抛物线上有一个动点P，当点P在该抛物线上滑动到什么位置时，满足S_△_PAB=8，并求出此时P点的坐标．

查看试题解析