贵州省黔东南苗族侗族自治州2022-2023学年九年级上学期期中数学试题

试卷更新日期：2022-12-26 类型：期中考试

进入出卷网下载

一、单选题

1. “保护生态，人人有责”．下列生态环保标志中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 将抛物线y=2x²+2向左平移3个单位长度，再向上平移2个单位长度，得到抛物线的解析式是（）

A、y=2(x+3)²+4 B、y=2(x+3)² C、y=2(x－3)²+4 D、y=2(x－3)²

查看试题解析
3. 把方程 $x^{2} - 6 x - 1 = 0$ 转化成 ${(x + m)}^{2} = n$ 的形式，则 $m$ ， $n$ 的值是（）

A、3，8 B、3，10 C、-3，3 D、-3，10

查看试题解析
4. 已知点A（1，2）与点 $A^{'} （ a ， b ）$ 关于坐标原点对称，则实数a、b的值是（）

A、a＝1，b＝2 B、a＝-1，b＝2 C、a＝1，b＝-2 D、a＝-1，b＝-2

查看试题解析
5. 如图，△ODC是由△OAB绕点O顺时针旋转31°后得到的图形，若点D恰好落在AB上，且∠AOC的度数为100°，则∠DOB的度数是（　　）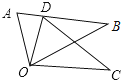

A、34° B、36° C、38° D、40°

查看试题解析
6. 已知关于x的一元二次方程（m﹣1）x²+2x﹣3＝0有实数根，则m的取值范围是（）

A、m≥ $\frac{2}{3}$ B、m＜ $\frac{2}{3}$ C、m＞ $\frac{2}{3}$ 且m≠1 D、m≥ $\frac{2}{3}$ 且m≠1

查看试题解析
7. 等腰△ABC的一边长为4，另外两边的长是关于x的方程x²−10x+m=0的两个实数根，则m的值是（）

A、24 B、25 C、26 D、24或25

查看试题解析
8. 已知 $(- 4 ， y_{1})$ ， $(2.5 ， y_{2})$ ， $(5 ， y_{3})$ 是抛物线 $y = - 3 x^{2} - 6 x + m$ 上的点，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系是（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{3} > y_{2} > y_{1}$ C、 $y_{1} > y_{3} > y_{2}$ D、 $y_{2} > y_{1} > y_{3}$

查看试题解析
9. 在同一坐标系中，二次函数 $y = a x^{2} + b x$ 与一次函数 $y = b x - a$ 的图像可能是（）

A、 B、 C、 D、

查看试题解析
10. 2022年北京冬奥会吉祥物“冰墩墩”意喻敦厚、健康、活泼、可爱，象征着冬奥会运动员强壮的身体、坚韧的意志和鼓舞人心的奥林匹克精神，随着北京冬奥会开幕日的临近，某特许零售店“冰墩墩”的销售日益火爆，据统计，该店2021年第四季度的“冰墩墩”总销售额为9.93万件，其中10月的销量为3万件，设11，12月份的平均增长率为 $x$ ，则可列方程为 $($ $)$

A、 $3 {(1 + x)}^{2} = 9.93$ B、 $3 + 3 {(1 + x)}^{2} = 9.93$ C、 $3 + 3 x + 3 {(1 + x)}^{2} = 9.93$ D、 $3 + 3 (1 + x) + 3 {(1 + x)}^{2} = 9.93$

查看试题解析
11. 如图，边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB₁C₁D₁ ，边B₁C₁与CD交于点O，则四边形AB₁OD的面积是（）

A、 $\frac{3}{4}$ B、 $\frac{\sqrt{2} - 1}{2}$ C、 $\sqrt{2} - 1$ D、 $1 + \sqrt{2}$

查看试题解析
12. 抛物线y＝ax²＋bx＋c上部分点的横坐标x，纵坐标y的对应值如下表：
x
…
-2
-1
0
1
2
…
y
…
0
4
6
6
4
…
从表中可知，下列说法中正确的是（）

A、抛物线的对称轴是直线x＝0 B、抛物线与x轴的一个交点为（3，0） C、函数y＝ax²＋bx＋c的最大值为6 D、在对称轴右侧，y随x增大而增大

查看试题解析

二、填空题

13. 一元二次方程x²﹣x＝0的根是．

查看试题解析
14. 如图，在矩形 $A B C D$ 中， $A B = 5$ ， $A D = 3$ .矩形 $A B C D$ 绕点 $A$ 逆时针旋转一定角度得到矩形 $A B^{^{'}} C^{^{'}} D^{^{'}}$ .若点 $B$ 的对应点 $B^{'}$ 落在边 $C D$ 上，则 $B^{'} C$ 的长为.

查看试题解析
15. 设a、b为 $x^{2} + x - 2021 = 0$ 的两个实数根，则 $a^{3} + a^{2} + 3 a + 2024 b$ ＝.

查看试题解析
16. 如图所示的抛物线是二次函数y＝（m-2）x²-3x+m²+m-6的图象，那么m的值是.

查看试题解析

三、解答题

17. 解一元二次方程.

(1)、 $x^{2} - 4 x - 7 = 0$

(2)、 $(2 x + 1)^{2} - 4 (2 x + 1) = 0$

查看试题解析
18. 用配方法把二次函数y=﹣2x²+6x+4化为y=a（x+m）²+k的形式，再指出该函数图象的开口方向、对称轴和顶点坐标．

查看试题解析
19. 如图所示，已知∠CAE＝65°，∠E＝70°，且AD⊥BC，如果△ABC经过旋转后与△ADE重合.

(1)、旋转中心是哪个点？

(2)、旋转了多少度？

(3)、∠BAC的度数是多少？

查看试题解析
20. 如图，在平面直角坐标系中，已知点 $B (4 ， 2)$ ， $B A ⊥ x$ 轴于A.
⑴画出将 $△ O A B$ 绕原点顺时针旋转 $9 0^{∘}$ 后所得的 $△ O A_{1} B_{1}$ ，并写出点 $A_{1}$ 、 $B_{1}$ 的坐标；
⑵画出 $△ O A B$ 关于原点O的中心对称图形 $△ O A_{2} B_{2}$ ，并写出点 $A_{2}$ 、 $B_{2}$ 的坐标.

查看试题解析
21. 如图，△BAD是由△BEC在平面内绕点B逆时针旋转60°而得，且AB⊥BC ， BE＝CE ，连接DE ．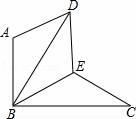

(1)、求证：△BDE≌△BCE；

(2)、试判断四边形ABED的形状．并说明理由．

查看试题解析
22. 某中学有一块长 $30 m$ ，宽 $20 m$ 的矩形空地，计划在这块空地面积的一半区域种花，其余部分硬化.如图所示，小亮同学设计了一个宽度相同的“U”形区域，求花带的宽度.

查看试题解析
23. 如图，直线y=﹣x+2过x轴上的点A（2，0），且与抛物线y=ax²交于B，C两点，点B坐标为（1，1）．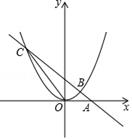

(1)、求抛物线的函数表达式；

(2)、连结OC，求出△AOC的面积．

(3)、当 -x+2＞ax²时，请观察图像直接写出x的取值范围.

查看试题解析
24. 某商店准备进一批季节性小家电，每个进价为40元，经市场预测，销售定价为50元，可售出400个；定价每增加1元，销售量将减少10个，设每个定价增加x元．

(1)、商店若想获得利润6000元，并且使进货量较少，则每个定价为多少元？应进货多少个？

(2)、用含x的代数式表示商店获得的利润W元，并计算商店若要获得最大利润，则每个应定价多少元？获得的最大利润是多少元？

查看试题解析
25. 如图，抛物线 $y = a x^{2} + 3 x + c (a \neq 0)$ 与 $x$ 轴交于点 $A (- 2 ， 0)$ 和点 $B$ ，与 $y$ 轴交于点 $C (0 ， 8)$ ，点 $P$ 为直线 $B C$ 上方抛物线上的动点，连接 $C P$ ， $P B$ ，直线 $B C$ 与抛物线的对称轴 $l$ 交于点 $E$ .

(1)、求抛物线的解析式；

(2)、求 $△ B C P$ 的面积最大值；

查看试题解析

x	…	-2	-1	0	1	2	…
y	…	0	4	6	6	4	…