福建省三明市将乐县2022-2023学年九年级上学期期中综合练习数学试题
试卷更新日期:2022-12-26 类型:期中考试
一、单选题
-
1. 在比例尺为1:10000的地图上,相距5cm的A,B两地的实际距离是( )A、500m B、500dm C、500cm D、500km2. 方程 的解是( )A、x=0 B、x=-1 C、x1=0,x2=-1 D、x1=0,x2=13. 菱形具有而矩形不一定具有的性质是 ( )
A、对角线互相垂直 B、对角线相等 C、对角线互相平分 D、对角互补4. 由下表估算一元二次方程x2+12x=15的一个根的范围,正确的是( )x
1.0
1.1
1.2
1.3
x2+12x
13
14.41
15.84
17.29
A、1.0<x<1.1 B、1.1<x<1.2 C、1.2<x<1.3 D、14.41<x<15.845. 学校新开设了航模、足球、绘画三个社团,如果晓晓和洋洋两名同学每人随机选择参加其中一个社团,那么晓晓和洋洋选到同一社团的概率为( )A、 B、 C、 D、6. 若 与 的相似比为1:4,则 与 的周长比为( )A、1:2 B、1:3 C、1:4 D、1:167. 如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( ) A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当∠ABC=90°时,它是矩形 D、当AC=BD时,它是正方形8. 某市2016年投入教育经费3亿元,为了发展教育事业,该市每年教育经费的年增长率均为x,从2016年到2018年共投入教育经费12.5亿元,则下列方程正确的是( )A、3x2=12.5 B、3(1+x)=12.5 C、3(1+x)2=12.5 D、3+3(1+x)+3(1+x)2=12.59. 如图,在△ABC中,点D、E分别是AB、AC的中点,则下列结论不正确的是( )
A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当∠ABC=90°时,它是矩形 D、当AC=BD时,它是正方形8. 某市2016年投入教育经费3亿元,为了发展教育事业,该市每年教育经费的年增长率均为x,从2016年到2018年共投入教育经费12.5亿元,则下列方程正确的是( )A、3x2=12.5 B、3(1+x)=12.5 C、3(1+x)2=12.5 D、3+3(1+x)+3(1+x)2=12.59. 如图,在△ABC中,点D、E分别是AB、AC的中点,则下列结论不正确的是( ) A、BC=2DE B、△ADE∽△ABC C、 D、S△ABC=3S△ADE10. 如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A、BC=2DE B、△ADE∽△ABC C、 D、S△ABC=3S△ADE10. 如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( ) A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→正方形→矩形
A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→正方形→矩形二、填空题
-
11. 若 ,则 的值为.12. 已知菱形的面积为24,一条对角线长为6,则这个菱形的另一条对角线长是 .13. 已知2+ 是方程x -4x+c=0的一个根,则方程的另一个根为 .14. 一次会议上,每两个参加会议的人都互相握手一次,有人统计一共是握了66次手,则这次会议到会人数是人.15. 方程 的两个根是等腰三角形的底和腰,则这个等腰三角形的周长为.16. 如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM、ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=4,BC=2.运动过程中点D到点O的最大距离是.

三、解答题
-
17. 按要求解方程(1)、用配方法解方程;(2)、用适当的方法解方程18. 在平面直角坐标系中,的三个顶点坐标分别为 , , .
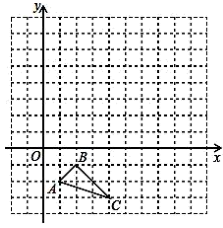
⑴画出关于轴对称的;
⑵以点为位似中心,在网格中画出的位似图形 , 使与的相似比为;
⑶设点为内一点,则依上述两次变换后点在内的对应点的坐标是 ▲ .
19. 一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外完全相同,其中红球1个,若从中随机摸出一个球,这个球是白球的概率为(1)、求袋子中白球的个数(2)、随机摸出一个球后,放回并搅匀,再随机摸出一个球,请用画树状图或列表的方法,求两次都摸到白球的概率.20. 已知关于x的一元二次方程x2﹣(2m﹣2)x+(m2﹣2m)=0.(1)、求证:方程有两个不相等的实数根.
(2)、如果方程的两实数根为x1 , x2 , 且x12+x22=10,求m的值.
21. 如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AE∥CD,CE∥AB,连接DE交AC于点O. (1)、证明:四边形ADCE为菱形.(2)、BC=6,AB=10,求菱形ADCE的面积.22. 某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件,为了迎接“双11”节,扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件.设每件降价x元.(1)、降价后每件利润元,商场能售出件.(2)、要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价多少元?23. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)、证明:四边形ADCE为菱形.(2)、BC=6,AB=10,求菱形ADCE的面积.22. 某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件,为了迎接“双11”节,扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件.设每件降价x元.(1)、降价后每件利润元,商场能售出件.(2)、要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价多少元?23. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.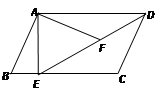 (1)、求证:△ADF∽△DEC(2)、若AB=4,AD=3 ,AE=3,求AF的长.24. 如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动.若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求:
(1)、求证:△ADF∽△DEC(2)、若AB=4,AD=3 ,AE=3,求AF的长.24. 如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动.若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求: (1)、经过6秒后,BP=cm,BQ=cm;(2)、经过几秒后,△BPQ是直角三角形?(3)、经过几秒△BPQ的面积等于 cm2?25. 已知:E是矩形的边上一个动点,直线交于点F,
(1)、经过6秒后,BP=cm,BQ=cm;(2)、经过几秒后,△BPQ是直角三角形?(3)、经过几秒△BPQ的面积等于 cm2?25. 已知:E是矩形的边上一个动点,直线交于点F, (1)、求证:;(2)、若直线经过C点,且 , 是否存在这样的点E,使和相似?若存在,请求出的长度;若不存在,请说明理由.(3)、连结 , 若 , 当和相似时,则.
(1)、求证:;(2)、若直线经过C点,且 , 是否存在这样的点E,使和相似?若存在,请求出的长度;若不存在,请说明理由.(3)、连结 , 若 , 当和相似时,则.