福建省三明市大田县2022-2023学年七年级上学期期中质量检测数学试题

试卷更新日期：2022-12-26 类型：期中考试

进入出卷网下载

一、单选题

1. $| - 2 |$ 等于（）

A、2 B、-2 C、 $\frac{1}{2}$ D、0

查看试题解析
2. 下列代数式书写规范的是（）

A、 $1 \frac{2}{3} a$ B、 $2 m \div n$ C、 $a \times 5$ D、 $2 x^{2} y$

查看试题解析
3. 下面几何体的截面不可能是长方形的是（）

A、长方体 B、正方体 C、圆锥 D、圆柱

查看试题解析
4. 下列各式中，正确的是（）

A、 $a^{3} + a^{2} = a^{5}$ B、 $2 a + 3 b = 5 a b$ C、 $3 a b - 2 a b = 1$ D、 $2 a^{2} b - 3 a^{2} b = - a^{2} b$

查看试题解析
5. 在 $- (- 2)$ ， $- (- 2)^{2}$ ， ${(- \frac{1}{3})}^{4}$ ， $- (- 1)^{2023}$ ， $- | - 2 |$ 中，正数的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
6. 下列各式中与a﹣b﹣c的值不相等的是（）

A、a﹣（b+c） B、a+（﹣b﹣c） C、a﹣（b﹣c） D、（﹣c）+（a﹣b）

查看试题解析
7. $1 - 2 + 3 - 4 + 5 - 6 + \dots + 2021 - 2022 =$ （）

A、－1011 B、1011 C、－1012 D、1012

查看试题解析
8. 一个骰子相对两面的点数之和为 $7$ ，它的展开图如图，下列判断正确的是（）

A、 $B$ 代表 B、 $B$ 代表 C、 $B$ 代表 D、 $B$ 代表

查看试题解析
9. 如图，A，B，C三点在数轴上所表示的数分别为a、b、c，根据图中各点位置，下列各式正确的是 $($ $)$

A、 $(a - 1) (b - 1) > 0$ B、 $(c - 1) (b - 1) > 0$ C、 $(a + 1) (b + 1) < 0$ D、 $(c + 1) (b + 1) < 0$

查看试题解析
10. 将正整数按如图所示的规律排列下去，若有序数对 $(n ， m)$ 表示第n排，从左到右第m个数，如 $(4 ， 2)$ 表示9，则表示2022的有序数对是（）

A、 $(64 ， 6)$ B、 $(63 ， 59)$ C、 $(64 ， 6)$ D、 $(64 ， 59)$

查看试题解析

二、填空题

11. 《九章算术》中注有“今两算得失相反，要另正负以名之”，意思是：今有两数若其意义相反，则分别叫做正数与负数.有一种记分法：85分以上，如88分记作+3分，某同学得分80分，则应记作分.

查看试题解析
12. 兴泉铁路大田客运站站前广场及站前路建设项目是省市重点项目，也是大田县委县政府为民办实事项目，项目总用地面积140000万平方米，总投资265000000元，其中265000000元这个数用科学记数法表示为元.

查看试题解析
13. 若一个棱柱有12个顶点，则这个棱柱有个侧面.

查看试题解析
14. 一个长方形周长为 $30 m$ ，若一边长用字母x表示，则另一边长为 m.

查看试题解析
15. 数a，b在数轴上对应点的位置如图所示，化简a-|b-a|= .

查看试题解析
16. 古希腊数学家把数1，3，6，10，15，21，…叫做三角数，它有一定的规律性.若把第一个三角数记为 $a_{1}$ ，第二个三角数记为 $a_{2}$ ， …，第n个三角数记为 $a_{n}$ ，则 $a_{n - 1} + a_{n} =$ （ $n > 1$ ）.

查看试题解析

三、解答题

17. 计算：

(1)、 $- 11 + (- 18) - (- 9) + (+ 12)$

(2)、 $- 1^{4} - (\frac{2}{7} - 0.5) \div \frac{1}{14} + (- 3)^{3}$ .

查看试题解析
18. 请你将0，-2， $- \frac{1}{2}$ ， $2^{2}$ ， $- (- 3)$ 在数轴上表示出来，并用“＞”将上列各数连接起来.

查看试题解析
19. 化简：

(1)、3s²-2s-2s²+5s

(2)、 $4 (x^{2} - x y + 6) - 3 (2 x^{2} + x y)$

查看试题解析
20. 如图，一个边长为10cm的无盖正方体可以展开成下面的平面图形.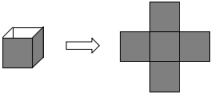

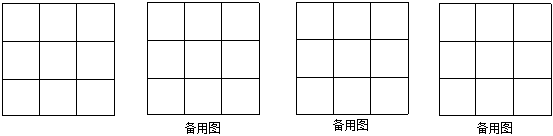(1)、这个表面展开图的面积是cm²；

(2)、将一个无盖正方体展开成平面图形的过程中，需要剪开条棱；

(3)、你还能在下面小方格中画出无盖正方体的其他不同形状的表面展开图吗？请画出所有可能的图形（把需要的小正方形涂上阴影）.

查看试题解析
21. 先化简，再求值：4a²＋（7a²－7a）－7（a²－a），其中 $a = - \frac{1}{2}$ .

查看试题解析
22. 某自行车厂计划一周生产自行车700辆，平均每天生产100辆，但由于种种原因，实际每天生产量与计划量相比有出入，下表是某周的生产情况（超产记为“ $+$ ”，减产记为“ $-$ ”）：
星期
一
二
三
四
五
六
日
增减（辆）
+5
-2
-4
+13
-10
+16
-9

(1)、根据记录的数据可知，该厂前四天共生产自行车辆；

(2)、根据记录的数据，产量最多的一天比产量最少的一天多生产辆；

(3)、该厂实行每周计件工资制，每生产一辆车可得50元，若每周超额完成任务，则超过部分每辆另奖励20元，少生产一辆扣10元，则该厂工人这一周的工资总额是多少元？

查看试题解析
23. 2022年秋季因我县七年级生源的增加，某校计划添置100张课桌和一批椅子（椅子不少于100把），现从A、B两家公司了解到：同一款式的产品价格相同，课桌每张300元，椅子每把100元.且A公司的优惠政策为：每买一张课桌赠送一把椅子，其余部分按原价结算；B公司的优惠政策为：课桌和椅子都实行8折优惠.

(1)、若购买课桌的同时买x把椅子，到A公司和B公司购买分别需要付款多少元？

(2)、如果购买课桌的同时买150把椅子，并且可以到A、B两公司分别购买，请你设计一种购买方案，使所付金额最少.

查看试题解析
24. 观察下列两个等式： $2 - \frac{1}{3} = 2 \times \frac{1}{3} + 1$ ， $5 - \frac{2}{3} = 5 \times \frac{2}{3} + 1$ ，给出定义如下：我们称使等式 $a - b = a b + 1$ 成立的一对有理数 $a ， b$ 为“共生有理数对”，记为 $(a ， b)$ ，如数对 $(2 ， \frac{1}{3})$ ， $(5 ， \frac{2}{3})$ ，都是“共生有理数对”.

(1)、判断数对 $(3 ， \frac{1}{2})$ 是否为“共生有理数对”，并说明理由；

(2)、若 $(m ， n)$ 是“共生有理数对”，且 $m n = 3$ ，求 $(- 2)^{m - n}$ 的值.

(3)、若 $(m ， - n)$ 是“共生有理数对”，则 $(2 n ， - 2 m)$ 是“共生有理数对”吗？请说明理由.

查看试题解析
25. 如图

(1)、【操作感知】如图①，长方形透明纸上有一条数轴， $A B$ 是周长为4的圆的直径，点 $A$ 与数轴原点重合，将圆从原点出发沿数轴正方向滚动1周，点 $A$ 落在数轴上的点 $A^{'}$ 处；将圆从原点出发沿数轴负方向滚动半周，点 $B$ 落在数轴上的点 $B^{'}$ 处，折叠长方形透明纸，使数轴上的点 $A^{'}$ 与点 $B^{'}$ 重合，此时折痕与数轴交点表示的数为.

(2)、【建立模型】折叠长方形透明纸，使得数轴上表示数 $a$ 的点 $M$ 与表示数 $b$ 的点 $N$ 重合，则折痕与数轴交点表示的数为（用含 $a$ ， $b$ 的代数式表示）.

(3)、【问题解决】若 $C$ ， $D$ ， $E$ 为数轴上不同的三点，点 $C$ 表示的数为 $4$ ，点 $D$ 表示的数为-2，如果 $C$ ， $D$ ， $E$ 三点中的一点到其余两点的距离相等，求点 $E$ 表示的数；

(4)、如图②，若 $A B$ 是周长为 $3$ 的圆的直径，点 $A$ 与数轴原点重合，将圆从原点出发沿数轴正方向滚动2周，点 $A$ 落在数轴上的点 $Q$ 处；将圆从原点出发沿数轴负方向滚动 $1$ 周，点 $A$ 落在数轴上的点 $P$ 处.将此长方形透明纸沿 $P$ ， $Q$ 剪开，将点 $P$ ， $Q$ 之间一段透明纸对折，使其左、右两端重合，这样连续对折 $n$ 次后，再将其展开，求最右端折痕与数轴交点表示的数.

查看试题解析

星期	一	二	三	四	五	六	日
增减（辆）	+5	-2	-4	+13	-10	+16	-9