福建省三明市大田县2022-2023学年九年级上学期期中质量检测数学试题
试卷更新日期:2022-12-26 类型:期中考试
一、单选题
-
1. 已知在某地图上A、B两地之间的距离为 , 这两地的实际距离为 , 则该地图的比例尺为( )A、 B、 C、 D、2. 用公式法解方程时,求根公式中的 , , 的值分别是( )A、 , , B、 , , C、 , , D、 , ,3. 如图,AD∥BE∥CF,AB=3,BC=6,DE=2,则EF的值为( )
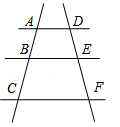 A、2 B、3 C、4 D、54. 以下条件中能判定平行四边形为菱形的是( )A、 B、 C、 D、5. 某篮球队员在一次训练中共投篮次,命中了其中的次,该运动员在这次训练中投篮命中的频率为( )A、0.64 B、0.8 C、1.25 D、646. 如图,在中,点 , , 分别是 , , 的中点.若的面积为 , 则的面积为( )
A、2 B、3 C、4 D、54. 以下条件中能判定平行四边形为菱形的是( )A、 B、 C、 D、5. 某篮球队员在一次训练中共投篮次,命中了其中的次,该运动员在这次训练中投篮命中的频率为( )A、0.64 B、0.8 C、1.25 D、646. 如图,在中,点 , , 分别是 , , 的中点.若的面积为 , 则的面积为( ) A、 B、 C、2 D、47. 受国际油价影响,今年我国汽油价格总体呈上升趋势.已知某地92号汽油六月底的价格是7.5元/升,八月底的价格是8.4元/升.设该地92号汽油价格这两个月每月的平均增长率为.根据题意列出方程,正确的是( )A、 B、 C、 D、8. 如图,是我国汉代数学家赵爽为了证明勾股定理构造的图形,后人称之为“赵爽弦图”.该图形由四个全等的直角三角形拼接而成,若 , , 则四边形的面积为( )
A、 B、 C、2 D、47. 受国际油价影响,今年我国汽油价格总体呈上升趋势.已知某地92号汽油六月底的价格是7.5元/升,八月底的价格是8.4元/升.设该地92号汽油价格这两个月每月的平均增长率为.根据题意列出方程,正确的是( )A、 B、 C、 D、8. 如图,是我国汉代数学家赵爽为了证明勾股定理构造的图形,后人称之为“赵爽弦图”.该图形由四个全等的直角三角形拼接而成,若 , , 则四边形的面积为( ) A、25 B、49 C、64 D、1449. 已知 , 是方程的两个实根,则的值为( )A、9 B、10 C、11 D、2110. 如图,在平面直角坐标系中,直线交轴于点 , 交轴于点 , 点是线段上的动点,过作轴,轴的垂线,垂足分别为 , , 连结.当最小时,( )
A、25 B、49 C、64 D、1449. 已知 , 是方程的两个实根,则的值为( )A、9 B、10 C、11 D、2110. 如图,在平面直角坐标系中,直线交轴于点 , 交轴于点 , 点是线段上的动点,过作轴,轴的垂线,垂足分别为 , , 连结.当最小时,( ) A、 B、2 C、3 D、
A、 B、2 C、3 D、二、填空题
-
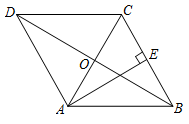
11. 非零实数 , 满足 , 则.12. 正方形的对称中心为点 , 若 , 则该正方形的周长为.13. 如图,在菱形中,对角线 , 的交点为 , , .若点在上,且 , 则的长为.
 14. 若实数 , 满足 , 则代数式的最小值为.15. 将2,3,4,6这四个数随机排列,排列结果记为 , , , .则 , , , 成比例的概率为.16. 如图,在中, , 点 , 在线段上,且 , 将线段绕点顺时针旋转后得到线段 , 连接 , .给出以下结论:
14. 若实数 , 满足 , 则代数式的最小值为.15. 将2,3,4,6这四个数随机排列,排列结果记为 , , , .则 , , , 成比例的概率为.16. 如图,在中, , 点 , 在线段上,且 , 将线段绕点顺时针旋转后得到线段 , 连接 , .给出以下结论:①;
②;
③;
④.
其中正确的是.(写出所有正确结论的序号)

三、解答题
-
17. 解下列方程:(1)、;(2)、.18. 已知 .(1)、若 , 求 , 的值;(2)、若 , 求的值.19. 如图,在平行四边形中,对角线 , 相交于点 , 且是等边三角形.
 (1)、证明:平行四边形是矩形;(2)、若 , 求矩形的面积.20. 已知方程的一个根为.(1)、求的值;(2)、设方程的另一个根为 , 求的值.21. 一个盒子中有2个红球和3个白球,这些球除颜色外都相同.从中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球.求:(1)、第一次摸到红球的概率;(2)、两次摸到不同颜色球的概率.22. 在菱形中,.(1)、以线段为边求作菱形;(要求:尺规作图,不写作法,保留作图痕迹)
(1)、证明:平行四边形是矩形;(2)、若 , 求矩形的面积.20. 已知方程的一个根为.(1)、求的值;(2)、设方程的另一个根为 , 求的值.21. 一个盒子中有2个红球和3个白球,这些球除颜色外都相同.从中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球.求:(1)、第一次摸到红球的概率;(2)、两次摸到不同颜色球的概率.22. 在菱形中,.(1)、以线段为边求作菱形;(要求:尺规作图,不写作法,保留作图痕迹) (2)、若菱形的面积为 , 求的长.23. 如图,在三边互不相等的中, , .动点从开始沿边运动,速度为秒,动点同时从点开始沿边运动,速度为秒,当点P到达点时, , 就不再运动.设 , 两点运动时间为秒,解决以下问题:
(2)、若菱形的面积为 , 求的长.23. 如图,在三边互不相等的中, , .动点从开始沿边运动,速度为秒,动点同时从点开始沿边运动,速度为秒,当点P到达点时, , 就不再运动.设 , 两点运动时间为秒,解决以下问题: (1)、证明:当时,;(2)、若与相似,求的值.24. 某单位准备举办羽毛球邀请赛,赛制为单循环(每两位选手之间各进行一场比赛),计划一共举行45场比赛.(1)、求该邀请赛的参赛选手人数;(2)、为了保证比赛正常进行,该单位需要为每场比赛至少准备4只羽毛球,且计划购买的羽毛球数量为10的整数倍.计划购买的某品牌羽毛球原价4元/只,现有甲,乙两家公司促销该品牌羽毛球.甲公司促销方案:在原价的基础上,在一定范围内每多购买10只,每个的单价可降低0.05元,例如购买20只时的单价为3.9元,最低单价不能低于2.8元;乙公司一律按8折促销.若该单位选择甲,乙中的一家公司购买,经过计算发现,分别选择在这两家公司购买的总金额相差40元,从节约成本的角度考虑,判断该单位应选择哪家公司购买,并求其计划购买的羽毛球数量.25. 如图,在平面直角坐标系中,矩形的边 , 分别在轴,轴上,且点的坐标为.是边上的动点,以为一边在其右侧作矩形 , 其中 , 连结 , .
(1)、证明:当时,;(2)、若与相似,求的值.24. 某单位准备举办羽毛球邀请赛,赛制为单循环(每两位选手之间各进行一场比赛),计划一共举行45场比赛.(1)、求该邀请赛的参赛选手人数;(2)、为了保证比赛正常进行,该单位需要为每场比赛至少准备4只羽毛球,且计划购买的羽毛球数量为10的整数倍.计划购买的某品牌羽毛球原价4元/只,现有甲,乙两家公司促销该品牌羽毛球.甲公司促销方案:在原价的基础上,在一定范围内每多购买10只,每个的单价可降低0.05元,例如购买20只时的单价为3.9元,最低单价不能低于2.8元;乙公司一律按8折促销.若该单位选择甲,乙中的一家公司购买,经过计算发现,分别选择在这两家公司购买的总金额相差40元,从节约成本的角度考虑,判断该单位应选择哪家公司购买,并求其计划购买的羽毛球数量.25. 如图,在平面直角坐标系中,矩形的边 , 分别在轴,轴上,且点的坐标为.是边上的动点,以为一边在其右侧作矩形 , 其中 , 连结 , . (1)、证明:;(2)、当点点坐标为时,求点的坐标;(3)、证明点的运动范围是一条线段,并求该线段的长.
(1)、证明:;(2)、当点点坐标为时,求点的坐标;(3)、证明点的运动范围是一条线段,并求该线段的长.