福建省三明市大田县2022-2023学年八年级上学期期中质量检测数学试题
试卷更新日期:2022-12-26 类型:期中考试
一、单选题
-
1. 在实数中,最小的实数是( )A、 B、0 C、-1 D、32. 在平面直角坐标系中,点 位于哪个象限?( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 的相反数是( )A、 B、 C、 D、4. 如果影剧院的座位8排5座用(8,5)表示,那么(4,6)表示( )A、6排4座 B、4排6座 C、4排4座 D、6排6座5. 下列各组数中,不是勾股数的是( )A、3,4,5 B、5,12,13 C、8,9,10 D、9,40,416. 若面积为15的正方形的边长为x,则x的范围是( )A、 B、 C、 D、7. 一根蜡烛长30cm,点燃后每小时燃烧5cm,燃烧时蜡烛剩余的长度h(cm)和燃烧时间t(小时)之间的函数关系用图像可以表示为中的( )A、
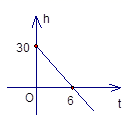 B、
B、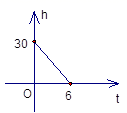 C、
C、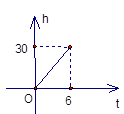 D、
D、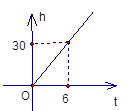 8. 把直线向下平移3个单位长度,得到的直线的表达式为( )A、 B、 C、 D、9. 直角三角形的一条直角边长是8cm,另一条直角边比斜边短2cm,则斜边长为( )A、12 cm B、15 cm C、17 cm D、20 cm10. 下列表示一次函数与正比例函数(m、n为常数,且mn≠0)图象中,一定不正确的是( )A、
8. 把直线向下平移3个单位长度,得到的直线的表达式为( )A、 B、 C、 D、9. 直角三角形的一条直角边长是8cm,另一条直角边比斜边短2cm,则斜边长为( )A、12 cm B、15 cm C、17 cm D、20 cm10. 下列表示一次函数与正比例函数(m、n为常数,且mn≠0)图象中,一定不正确的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 一次函数中,y的值随x值增大而.(填“增大”或“减小”)12. 已知 , 则的值是.13. 若直角三角形其中两条边的长分别为3,4,则该直角三角形斜边上的高的长为 .14. 在平面直角坐标系中,点A(x,4),B(0,8)和C(-4,0)在同一直线上,则x= .15. 中国象棋是中华民族的文化瑰宝,它渊远流长,趣味浓厚.如图,在某平面直角坐标系中,如果
 所在位置的坐标为 ,
所在位置的坐标为 ,  所在位置的坐标为 , 那么
所在位置的坐标为 , 那么 所在位置的坐标为.
所在位置的坐标为. 16. 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图,如果大正方形的面积是49,小正方形的面积为4,直角三角形的较长直角边长为 , 较短直角边长为 , 下列四个说法:①②③④其中正确的是.
16. 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图,如果大正方形的面积是49,小正方形的面积为4,直角三角形的较长直角边长为 , 较短直角边长为 , 下列四个说法:①②③④其中正确的是.
三、解答题
-
17. 计算:(1)、;(2)、.18. 已知:与成正比例,且当 时,(1)、求与之间的函数表达式;(2)、当时,的值是多少?19. 把下列各数填入相应的括号内:(1)、无理数:{ …};(2)、负实数:{ …};(3)、整 数:{ …};(4)、分 数:{ …};20. 《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,在 中, ,求 的长.
 21. 如图,在的方格(每小格边长为1)上沿着网格线运动,规定:向上、向右为正,向下、向左为负.例如:从A到B记为: , 从B到A记为: , 其中第一个数表示左右方向,第二个数表示上下方向.
21. 如图,在的方格(每小格边长为1)上沿着网格线运动,规定:向上、向右为正,向下、向左为负.例如:从A到B记为: , 从B到A记为: , 其中第一个数表示左右方向,第二个数表示上下方向. (1)、图中A→C( , ),C→B( , ).(2)、若运动路线为: , , 请在图中标出点的位置;(3)、若图中格点处另有三点,且 , 则N→P( , ).22. 如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中 , 由于某些原因,由C到A的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点H(A,H,B在同一条直线上),并新修一条路 , 测得千米,千米,千米.
(1)、图中A→C( , ),C→B( , ).(2)、若运动路线为: , , 请在图中标出点的位置;(3)、若图中格点处另有三点,且 , 则N→P( , ).22. 如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中 , 由于某些原因,由C到A的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点H(A,H,B在同一条直线上),并新修一条路 , 测得千米,千米,千米. (1)、是否是从村庄C到河边最近的路?请通过计算加以说明.(2)、原路比新路多多少千米?23. 我们知道, , , …如果两个含有二次根式的非零代数式相乘,它们的积不含有二次根式,就说这两个非零代数式互为有理化因式.如与互为有理化因式.利用这种方法,可以将分母中含有二次根式的代数式化为分母是有理数的代数式,这个过程称为分母有理化,例如: , .(1)、分母有理化的结果是;(2)、分母有理化的结果是;(3)、分母有理化的结果是;(4)、利用以上知识计算:.24. 如图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形实心铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽中的水匀速注入乙槽,甲、乙两个水槽中水的深度与注水时间之间的关系如图2.根据图象提供的信息,解答下列问题:
(1)、是否是从村庄C到河边最近的路?请通过计算加以说明.(2)、原路比新路多多少千米?23. 我们知道, , , …如果两个含有二次根式的非零代数式相乘,它们的积不含有二次根式,就说这两个非零代数式互为有理化因式.如与互为有理化因式.利用这种方法,可以将分母中含有二次根式的代数式化为分母是有理数的代数式,这个过程称为分母有理化,例如: , .(1)、分母有理化的结果是;(2)、分母有理化的结果是;(3)、分母有理化的结果是;(4)、利用以上知识计算:.24. 如图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形实心铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽中的水匀速注入乙槽,甲、乙两个水槽中水的深度与注水时间之间的关系如图2.根据图象提供的信息,解答下列问题: (1)、图2中折线表示槽中水的深度与注水时间之间的关系,线段表示槽中水的深度与注水时间之间的关系(以上两空填“甲”或“乙”),槽中铁块的高度是;(2)、注水多长时间时,甲、乙两个水槽中水的深度相同;(3)、若乙槽底面积为(壁厚不计),求乙槽中铁块的体积.25. 如图1,在同一平面直角坐标系中,直线:与直线:相交于点 , 与x轴交于点 , 直线与轴交于点.
(1)、图2中折线表示槽中水的深度与注水时间之间的关系,线段表示槽中水的深度与注水时间之间的关系(以上两空填“甲”或“乙”),槽中铁块的高度是;(2)、注水多长时间时,甲、乙两个水槽中水的深度相同;(3)、若乙槽底面积为(壁厚不计),求乙槽中铁块的体积.25. 如图1,在同一平面直角坐标系中,直线:与直线:相交于点 , 与x轴交于点 , 直线与轴交于点. (1)、填空: = , = , = ;(2)、如图2,点为线段上一动点,将△沿直线翻折得到△ , 线段交轴于点.
(1)、填空: = , = , = ;(2)、如图2,点为线段上一动点,将△沿直线翻折得到△ , 线段交轴于点.① 当点落在轴上时,求点的坐标;
② 若△为直角三角形,求点的坐标.