福建省龙岩市上杭县西北片区联考2022-2023学年九年级上学期期中数学试题

试卷更新日期：2022-12-26 类型：期中考试

进入出卷网下载

一、单选题

1. 2022年2月第24届冬季奥林匹克运动会在我国北京成功举办，以下是参选的冬奥会会徽设计的部分图形，其中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 方程 $x^{2} = 2 x$ 的的解为（）

A、 $x = 0$ B、 $x = 2$ C、 $x = 0$ 或 $x = 2$ D、 $x = 0$ 或 $x = - 2$

查看试题解析
3. 关于 $x$ 一元二次方程 $(a - 1) x^{2} + x + a^{2} - 1 = 0$ 的一个根是0，则 $a$ 的值为（）

A、1或-1 B、1 C、-1 D、0

查看试题解析
4. 若方程 $m x^{2} + 2 x + 1 = 0$ 有实数根，则 $m$ 的取值范围是（）

A、 $m \leq 1$ B、 $m \leq 1$ 且 $m \neq 0$ C、 $m ＜ 1$ D、 $m ＜ 1$ 且 $m \neq 0$

查看试题解析
5. 二次函数y= - 3(x-2)²-1的图象的顶点坐标是（）

A、（-2，1） B、（2，1） C、（-2，-1） D、（2，-1）

查看试题解析
6. 将抛物线y＝x²沿着x轴向左平移1个单位，再沿y轴向下平移1个单位，则得到的抛物线解析式为（）

A、y＝（x﹣1）²﹣1 B、y＝（x﹣1）²+1 C、y＝（x+1）²+1 D、y＝（x+1）²﹣1

查看试题解析
7. 关于抛物线 $y = x^{2} - 4 x + 3$ ，下列说法错误的是（）

A、开口向上 B、对称轴是直线 $x = 2$ C、与y轴交点为 $(0 ， 3)$ D、与坐标轴有2个交点

查看试题解析
8. 一次足球联赛实行单循环比赛（每两支球队之间都比赛一场），计划安排15场比赛，设应邀请了x支球队参加联赛，则下列方程中符合题意的是（）

A、 $\frac{1}{2} x (x + 1) = 15$ B、 $\frac{1}{2} x (x - 1) = 15$ C、 $x (x + 1) = 15$ D、 $x (x - 1) = 15$

查看试题解析
9. 将 $△ A B C$ 绕点A逆时针旋转一定的角度后，得到 $△ A D E$ ，且点B的对应点D恰好落在 $B C$ 边上，若 $∠ B = 70 °$ ，则 $∠ C A E$ 的度数是（）

A、70° B、50° C、40° D、30°

查看试题解析
10. 二次函数y=ax²+bx+c的图象如图所示，对称轴是x=－1．有以下结论：①abc>0，②4ac<b² ， ③2a+b=0，④a－b+c>2，其中正确的结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 关于 $x$ 的方程 $(m - 2) x^{m^{2} - 2} - x - 1 = 0$ 是一元二次方程，则 $m =$ .

查看试题解析
12. 在平面直角坐标系中，点 $(a + 2 ， 2)$ 关于原点的对称点为 $(4 ， - b)$ ，则 $a b$ 的值为.

查看试题解析
13. 已知 $m$ 、 $n$ 是方程 $x^{2} - x - 3 = 0$ 的两根，则 $m^{2} + m n - 2 m - n =$ .

查看试题解析
14. 已知方程 $a x^{2} + b x + c = 0$ 的两个根为1和-3，则抛物线 $y = a x^{2} + b x + c$ 的对称轴为直线.

查看试题解析
15. 线段 $O A$ 在平面直角坐标系内，A点坐标为 $(2 ， 5)$ ，线段 $O A$ 绕原点O逆时针旋转 $90 °$ ，得到线段 $O A^{^{'}}$ ，则点 $A^{'}$ 的坐标为.

查看试题解析
16. 已知二次函数 $y = {(x - 1)}^{2} + m$ 的图象上有三点 $A (1.5 ， y_{1})$ ， $B (2 ， y_{2})$ ， $C (- 1 ， y_{3})$ 则 $y_{1} 、 y_{2} 、 y_{3}$ 的大小关系为.

查看试题解析

三、解答题

17. 用适当的方法解下列方程：

(1)、 $x^{2} - 2 x - 3 = 0$ .

(2)、 ${(x - 2)}^{2} = 3 x - 6$

查看试题解析
18. 已知关于x的一元二次方程 $x^{2} + 3 x + k - 2 = 0$ 有实数根．

(1)、求实数k的取值范围．

(2)、设方程的两个实数根分别为 $x_{1} ， x_{2}$ ，若 $(x_{1} + 1) (x_{2} + 1) = - 1$ ，求k的值．

查看试题解析
19. 为响应市委市政府提出的建设“绿色襄阳”的号召，我市某单位准备将院内一块长30m，宽20m的长方形空地，建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道，剩余的地方种植花草，如图所示，要使种植花草的面积为532m² ，那么小道进出口的宽度应为多少米？（注：所有小道进出口的宽度相等，且每段小道均为平行四边形）

查看试题解析
20. 如图，在足够大的空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，其中AD≤MN，已知矩形菜园的一边靠墙，另三边一共用了100米木栏．

(1)、若a=20，所围成的矩形菜园的面积为450平方米，求所利用旧墙AD的长；

(2)、求矩形菜园ABCD面积的最大值．

查看试题解析
21. 如图， $△ A B C$ 的三个顶点都在边长为1的小正方形组成的网格的格点上，以点 $O$ 为原点建立直角坐标系，回答下列问题：
⑴将 $△ A B C$ 先向上平移5个单位，再向右平移1个单位得到 $△ A_{1} B_{1} C_{1}$ ，画出 $△ A_{1} B_{1} C_{1}$ ，并直接写出 $A_{1}$ 的坐标 ▲ ；
⑵将 $△ A_{1} B_{1} C_{1}$ 绕点 $(0 ， - 1)$ 顺时针旋转90°得到 $△ A_{2} B_{2} C_{2}$ ，画出 $△ A_{2} B_{2} C_{2}$ ；
⑶观察图形发现， $△ A_{2} B_{2} C_{2}$ 是由 $△ A B C$ 绕点 ▲ （写出点的坐标）顺时针旋转 ▲ 度得到的.

查看试题解析
22. 某学校九年级的一场篮球比赛中，队员甲正在投篮，已知球出手时离地面高 $\frac{20}{9}$ m，与篮圈中心的水平距离为7m，当球出手后水平距离为4m时到达最大高度4m.如图，设篮球运行轨迹为抛物线，篮圈距地面3m.

(1)、建立如图所示的平面直角坐标系，问此球能否准确投中？

(2)、此时，若对方队员乙在甲前面1m处跳起盖帽拦截，已知乙的最大摸高为3.1m，那么他能否获得成功？

查看试题解析
23. 已知抛物线 $y = - x^{2} + (m - 1) x + m$ 图象上一点 $(1 ， 4)$ .

(1)、求 $m$ 的值；

(2)、求抛物线与 $x$ 轴的交点坐标；

(3)、画出这条抛物线大致图象（草图），并根据图象回答：
① 当 $x$ 取什么值时，y＞0 ？

② 当 $x$ 取什么值时，y的值随 $x$ 的增大而减小？

查看试题解析
24. 在Rt△ABC中，∠ABC=90°，∠BAC＝30°，将△ABC绕点A顺时针旋转一定的角度 $α$ 得到△AED ，点B、C的对应点分别是E、D.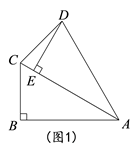

(1)、如图1，当点E恰好在AC上时，求∠CDE的度数；

(2)、如图2，若 $α$ =60°时，点F是边AC中点，求证：四边形BFDE是平行四边形.

查看试题解析
25. 如图，直线 $y = - \frac{1}{2} x + 2$ 交y轴于点A，交x轴于点C，抛物线 $y = - \frac{1}{4} x^{2} + b x + c$ 经过点A，点C，且交x轴于另一点B.

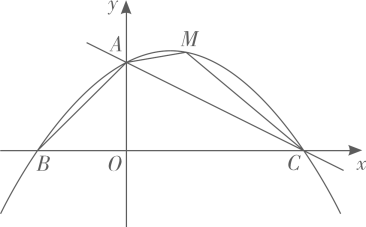(1)、直接写出点A，点B，点C的坐标及抛物线的解析式；

(2)、在直线 $A C$ 上方的抛物线上有一点M，求四边形 $A B C M$ 面积的最大值及此时点M的坐标；

(3)、将线段 $O A$ 绕x轴上的动点 $P (m ， 0)$ 顺时针旋转90°得到线段 $O^{'} A^{'}$ ，若线段 $O^{'} A^{'}$ 与抛物线只有一个公共点，请结合函数图象，求m的取值范围.

查看试题解析