福建省龙岩市上杭县西北片区联考2022-2023学年八年级上学期期中数学试题
试卷更新日期：2022-12-26 类型：期中考试
一、单选题
-
1. 下列图标中，是轴对称图的是（ ）A、
B、
C、
D、
2. 已知三角形的两边长分别为5和9，则该三角形的第三边长可能是（ ）A、3 B、4 C、5 D、143. 能把一个三角形的面积分成相等的两部分的线是这个三角形的（ ）A、一条高 B、一条中线 C、一条角平分线 D、一边上的中垂线4. 如图，在中， ， 则图中的度数是（ ）
A、180° B、240° C、220° D、300°5. 如图，点O是△ABC内一点，∠ABO=30°，∠ACO=15°，∠BOC=100°，则∠A的度数为（ ）
A、40° B、45° C、55° D、不能确定6. 如图OP平分∠AOB，PC⊥OA于C，D在OB上，PC=3，则PD的大小关系是（ ）
A、PD≥3 B、PD=3 C、PD≤3 D、不能确定7. 如图， ， 交于点C，于D，若 ， 则等于（ ）
A、3 B、2 C、1.5 D、18.如图，在△ABC和△DEC中，已知AB=DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是（ ）
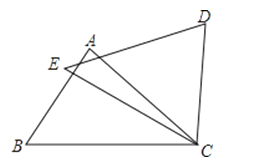A、BC=EC，∠B=∠E B、BC=EC，AC=DC C、BC=EC，∠A=∠D D、∠B=∠E，∠A=∠D9. 如图，过边长为的等边三角形的边上一点 ， 作于点为延长线上一点，当时，交于 ， 则的长为（ ）
A、 B、 C、 D、不能确定10. 如图，在△ABC中，∠ABC=45°，AD，BE分别为BC，AC边上的高，AD，BE相交于点F，连接CF，则下列结论：①BF=AC；②∠FCD=45°；③若BF=2EC，则△FDC周长等于AB的长；其中正确的有（ ）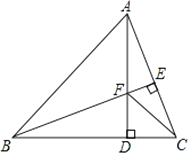
A、0个 B、1个 C、2个 D、3个二、填空题
-
11. 三角形的外角和为度.12. 点A（3，﹣2）关于x轴对称的点的坐标是 ．
13. 等腰三角形的一个内角是 ，则它的顶角度数是 ．14. 如图，△ABC中，D为AB上一点，E为BC上一点，且AC=CD=BD=BE，∠A=40°，则∠CDE的度数为 ．
15. 如图， 在平面直角坐标系中点A的坐标为 ， 点B为x轴上的动点，若为等腰三角形，则B点的位置有种.
16. 如图，∠AOB=30°，点P位于∠AOB内，OP=3，点M，N分别是射线OA、OB边上的动点，当△PMN的周长最小时，最小周长为.
三、解答题
-
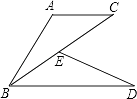
17. 一个多边形的内角和比四边形的内角和多720°，并且这个多边形的各内角都相等，这个多边形的每个内角是多少度？18. 已知：如图，E为BC上一点，AC∥BD，AC=BE，BC=BD．
求证：AB=DE．
19. 如图，在△ABC中，∠B=40°，∠C=110°.
(1)、画出下列图形：①BC边上的高AD；②∠A的角平分线AE.
(2)、试求∠DAE的度数.20. 如图，在平面直角坐标系中， ， ， ．
(1)、在图中作出关于轴对称的；(2)、写出点 ， ， 的坐标；(3)、求的面积．21. 如图， ， ， ， 平分 ， 若 ， 求的长.
22. 如图，已知BE⊥AC于E，CF⊥AB于F，BE、CF相交于点D，若BD=CD.求证：AD平分∠BAC.
23. 如图，已知AE⊥AB，AF⊥AC，AE＝AB，AF＝AC.求证：
(1)、EC＝BF；(2)、EC⊥BF.
