2022~2023学年沪科版数学九年级上册期末模拟检测卷(一)
试卷更新日期:2022-12-25 类型:期末考试
一、单选题(每题4分,共40分)
-
1. 对于二次函数y=3(x-2)2+1的图象,下列说法正确的是( )A、开口向下 B、顶点坐标是(2,1) C、对称轴是直线x=-2 D、与x轴有两个交点2. 在如图所示的肉眼成像的示意图中,可能没有蕴含下列哪项初中数学知识( )
 A、平行线的性质 B、相似三角形的判定 C、位似图形 D、旋转3. 如图,如果 , 那么添加下列一个条件后,仍不能确定的是( )
A、平行线的性质 B、相似三角形的判定 C、位似图形 D、旋转3. 如图,如果 , 那么添加下列一个条件后,仍不能确定的是( ) A、 B、 C、 D、4. 如图,点 是正方形 的边 边上的黄金分割点,且 > , 表示 为边长的正方形面积, 表示以 为长, 为宽的矩形面积, 表示正方形 除去 和 剩余的面积, : 的值为( )
A、 B、 C、 D、4. 如图,点 是正方形 的边 边上的黄金分割点,且 > , 表示 为边长的正方形面积, 表示以 为长, 为宽的矩形面积, 表示正方形 除去 和 剩余的面积, : 的值为( ) A、 B、 C、 D、5. 如图,坡角为α的斜坡上有一棵垂直于水平地面的大树AB,当太阳光线与水平线成45°角沿斜坡照下,在斜坡上的树影BC长为m,则大树AB的高为( )
A、 B、 C、 D、5. 如图,坡角为α的斜坡上有一棵垂直于水平地面的大树AB,当太阳光线与水平线成45°角沿斜坡照下,在斜坡上的树影BC长为m,则大树AB的高为( )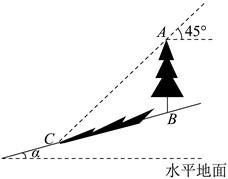 A、 B、 C、 D、6. 如图,矩形OABC与反比例函数(k1是非零常数,x>0)的图象交于点M,N,与反比例函数(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1-k2=( )
A、 B、 C、 D、6. 如图,矩形OABC与反比例函数(k1是非零常数,x>0)的图象交于点M,N,与反比例函数(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1-k2=( )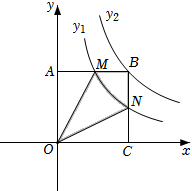 A、3 B、-3 C、 D、7. 在同一平面直角坐标系中,函数y=ax+b与y=ax2-bx的图象可能是( )A、
A、3 B、-3 C、 D、7. 在同一平面直角坐标系中,函数y=ax+b与y=ax2-bx的图象可能是( )A、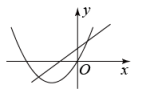 B、
B、 C、
C、 D、
D、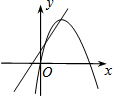 8. 如图,为的直径,弦交于点 , , , , 则( )
8. 如图,为的直径,弦交于点 , , , , 则( )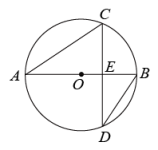 A、 B、 C、1 D、29. 已知如图, 在正方形中, 点的坐标分别是 , 点在抛物线 的图像上, 则的值是( )
A、 B、 C、1 D、29. 已知如图, 在正方形中, 点的坐标分别是 , 点在抛物线 的图像上, 则的值是( ) A、 B、 C、 D、10. 如图,在 中, , , ,且 ,若 ,点 是线段 上的动点,则 的最小值是( )
A、 B、 C、 D、10. 如图,在 中, , , ,且 ,若 ,点 是线段 上的动点,则 的最小值是( )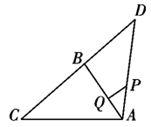 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题5分,共20分)
-
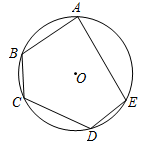
11. 已知某斜面的坡度为1: , 那么这个斜面的坡角等于度.12. 如图,点A,B,C,D,E都是⊙O上的点,AC=AE,∠D=128°,则∠B=°。
 13. 如图,人工喷泉有一个竖直的喷水枪 , 喷水口A距地面 , 喷出水流的运动路线是抛物线,如果水流的最高点P到喷水枪所在直线的距离为 , 且到地面的距离为 , 则水流的落地点C到水枪底部B的距离为m.
13. 如图,人工喷泉有一个竖直的喷水枪 , 喷水口A距地面 , 喷出水流的运动路线是抛物线,如果水流的最高点P到喷水枪所在直线的距离为 , 且到地面的距离为 , 则水流的落地点C到水枪底部B的距离为m. 14. 如图,在矩形中, , , 点为边上任意一点,将沿折叠,使点落在点处,连接 , 若是直角三角形,则线段的长为 .
14. 如图,在矩形中, , , 点为边上任意一点,将沿折叠,使点落在点处,连接 , 若是直角三角形,则线段的长为 .
三、综合题(共8题,共90分)
-
15. 如图,直线y=﹣x+2过x轴上的点A(2,0),且与抛物线y=ax2交于B,C两点,点B坐标为(1,1).
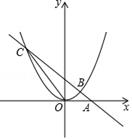 (1)、求抛物线的函数表达式;(2)、连结OC,求出△AOC的面积.(3)、当 -x+2>ax2 时,请观察图像直接写出x的取值范围.16. 以的速度在平地上将一小铁球沿与地面成角的方向击出时,小铁球的飞行路线是一条抛物线.如果不考虑空气的阻力,那么小铁球的飞行高度h(单位:米)与飞行时间t(单位:秒)之间的函数关系是: .(1)、小铁球飞行几秒时,小铁球的高度是25米?(2)、小铁球的飞行高度能否达到45米,若能,需要多少飞行时间?(3)、小铁球在空中飞行了多少时间?17. 如图,在中,C为上一点,且 , , 过点D作 , 交的延长线于点H.
(1)、求抛物线的函数表达式;(2)、连结OC,求出△AOC的面积.(3)、当 -x+2>ax2 时,请观察图像直接写出x的取值范围.16. 以的速度在平地上将一小铁球沿与地面成角的方向击出时,小铁球的飞行路线是一条抛物线.如果不考虑空气的阻力,那么小铁球的飞行高度h(单位:米)与飞行时间t(单位:秒)之间的函数关系是: .(1)、小铁球飞行几秒时,小铁球的高度是25米?(2)、小铁球的飞行高度能否达到45米,若能,需要多少飞行时间?(3)、小铁球在空中飞行了多少时间?17. 如图,在中,C为上一点,且 , , 过点D作 , 交的延长线于点H. (1)、求证∶ .(2)、若 , 求的长度.18. 如图,D是等腰三角形底边的中点,过点 作 .
(1)、求证∶ .(2)、若 , 求的长度.18. 如图,D是等腰三角形底边的中点,过点 作 .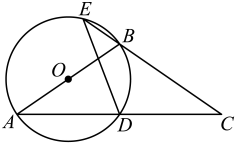 (1)、求证:是的直径;(2)、延长交于点E,连接 , 求证:;(3)、若 , , 求长.19. 如图,在△ABC中, .
(1)、求证:是的直径;(2)、延长交于点E,连接 , 求证:;(3)、若 , , 求长.19. 如图,在△ABC中, . (1)、先作AB的中点O,然后以OA为半径作 , 交AC于点D,过点D作 , 垂足为点E.(要求:尺规作图,保留作图痕迹,不写作法)(2)、若 , , 求此时DE的长.20. 为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理.如图所示,正在执行巡航任务的海监船以每小时50海里的速度向正东方向航行,在A处测得灯塔P在北偏东60°方向上,继续航行30分钟后到达B处,此时测得灯塔P在北偏东45°方向上.
(1)、先作AB的中点O,然后以OA为半径作 , 交AC于点D,过点D作 , 垂足为点E.(要求:尺规作图,保留作图痕迹,不写作法)(2)、若 , , 求此时DE的长.20. 为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理.如图所示,正在执行巡航任务的海监船以每小时50海里的速度向正东方向航行,在A处测得灯塔P在北偏东60°方向上,继续航行30分钟后到达B处,此时测得灯塔P在北偏东45°方向上.
(参考数据: ≈1.414, ≈1.732)
(1)、求∠APB的度数.(2)、已知在灯塔P的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?

