浙教版备考2023年中考数学一轮复习40.二次函数与一元二次方程
试卷更新日期:2022-12-25 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 根据以下表格中二次函数y=ax2+bx+c的自变量x与函数值y的对应值,可以判断方程ax2+bx+c=0的一个解x的范围是( )
x
0
0.5
1
1.5
2
y=ax2+bx+c
﹣1
﹣0.5
1
3.5
7
A、0<x<0.5 B、0.5<x<1 C、1<x<1.5 D、1.5<x<22. 抛物线的图象如图所示,则下列结论正确的是( ) A、 B、 C、 D、关于x的一元二次方程有两个不相等的实数根3. 设一元二次方程的两实数根分别为 , 且 , 则、满足( )A、 B、 C、 D、4. 下表是部分二次函数的自变量与函数值的对应值:
A、 B、 C、 D、关于x的一元二次方程有两个不相等的实数根3. 设一元二次方程的两实数根分别为 , 且 , 则、满足( )A、 B、 C、 D、4. 下表是部分二次函数的自变量与函数值的对应值:1
1.1
1.2
1.3
1.4
-1
-0.49
0.04
0.59
1.16
那么方程的一个根在( )范围之间。
A、4~1.1 B、1.1~1.2 C、1.2~1.3 D、1.3~1.45. 如图,已知关于x的一元二次方程的两根在数轴上对应的点分别在区域①和区域②,区域均含端点,则k的值可能是( ) A、-1 B、0 C、1 D、26. 已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x , y)的对应值如表所示,则方程ax2+bx+2.32=0的根是( )
A、-1 B、0 C、1 D、26. 已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x , y)的对应值如表所示,则方程ax2+bx+2.32=0的根是( )x
……
0
4
……
y
……
0.32
﹣2
0.32
……
A、0或4 B、1或5 C、 或4﹣ D、 或 ﹣27. 小颖用计算器探索方程ax2+bx+c=0的根,作出如图所示的图象,并求得一个近似根x=﹣3.4,则方程的另一个近似根(精确到0.1)为( ) A、4.4 B、3.4 C、2.4 D、1.48. 抛物线上部分点的横坐标 , 纵坐标的对应值如下表:
A、4.4 B、3.4 C、2.4 D、1.48. 抛物线上部分点的横坐标 , 纵坐标的对应值如下表:…
-2
-1
0
1
2
…
…
0
4
6
6
4
…
则下列说法中正确的个数是( )
①方程有两根为 , ;②抛物线与y轴的交点为;③抛物线的对称轴是直线;④抛物线开口向上;
A、1 B、2 C、3 D、49. 已知二次函数(m为常数)的图象与x轴的一个交点为 , 则关于x的一元二次方程的两个实数根是( )A、 , B、 , C、 , D、 ,10. 在平面直角坐标系xOy中,已知点M,N的坐标分别为 , , 若抛物线与线段MN有两个不同的交点,则a的取值范围是( )A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
①b>0;②a﹣b+c=0;③当x<﹣1或x>3时,y>0;④一元二次方程ax2+bx+c+1=0(a≠0)有两个不相等的实数根.
上述结论中正确的是 . (填上所有正确结论的序号)
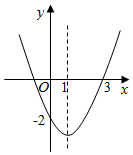 12. 已知函数 的图象如图所示,那么关于 的方程 有两个不相同的实数根,则 的取值范围是 .
12. 已知函数 的图象如图所示,那么关于 的方程 有两个不相同的实数根,则 的取值范围是 . 13. 二次函数y=ax2+bx+c(a≠0)的图象经过(﹣1,0),(0,4),(t,4)三点,当t≥3时,一元二次方程ax2+bx+c=n一定有实数根,则n的取值范围是 .14. 二次函数 (a≠0,a,b,c是常数)中,自变量x与函数y的对应值如下表:
13. 二次函数y=ax2+bx+c(a≠0)的图象经过(﹣1,0),(0,4),(t,4)三点,当t≥3时,一元二次方程ax2+bx+c=n一定有实数根,则n的取值范围是 .14. 二次函数 (a≠0,a,b,c是常数)中,自变量x与函数y的对应值如下表:x
-1
-
0
1
2
3
y
-2
1
2
1
-2
一元二次方程 (a≠0,a,b,c是常数)的两个根 的取值范围是下列选项中的哪一个 (填序号)
① ②
③ ④
15. 对于实数a,b,定义运算“*”:; , 关于x的方程 恰好有三个不相等的实数根,则m的取值范围是 .16. 已知二次函数y=a(x-x1)(x-x2)与x轴的交点是(1,0)和(3,0),关于x的方程a(x-x1)(x-x2)=m(m>0)的两个解分别为-1和5,关于x的方程a(x-x1)(x-x2)=n(其中m>n>0)也有两个整数解,则这两个整数解分别是 .三、解答题(共8题,共72分)
-
17. 若二次函数的对称轴为直线 , 求关于x的方程的解.18. 某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x
…
﹣3
﹣
﹣2
﹣1
0
1
2
3
…
y
…
3
m
﹣1
0
﹣1
0
3
…
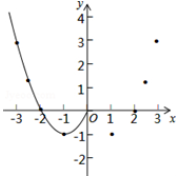 (1)、其中,m=.
(1)、其中,m=.
(2)、根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.(3)、观察函数图象,写出两条函数的性质.(4)、进一步探究函数图象发现:①函数图象与x轴有个交点,所以对应的方程x2﹣2|x|=0有个实数根;
②方程x2﹣2|x|=2有个实数根.

③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是.
19. 我们知道,可以借助于函数图象求方程的近似解.如图(甲),把方程x﹣2=1﹣x的解看成函数y=x﹣2的图象与函数y=1﹣x的图象的交点的横坐标,求得方程x﹣2=1﹣x的解为x=1.5. (1)、如图(乙),已画出了反比例函数在第一象限内的图象,借助于此图象求出方程2x2﹣2x﹣1=0的正数解.(要求画出相应函数的图象,结果精确到0.1)(2)、选择:三次方程x3﹣x2﹣2x+1=0的根的正负情况是 .A、有两个负根,一个正根 B、有三个负根 C、有一个负根,两个正根 D、有三个正根20. 利用图象解一元二次方程x2-2x-1=0时,我们采用的一种方法是在直角坐标系中画出抛物线y=x2和直线y=2x+1,两图象交点的横坐标就是该方程的解.
(1)、如图(乙),已画出了反比例函数在第一象限内的图象,借助于此图象求出方程2x2﹣2x﹣1=0的正数解.(要求画出相应函数的图象,结果精确到0.1)(2)、选择:三次方程x3﹣x2﹣2x+1=0的根的正负情况是 .A、有两个负根,一个正根 B、有三个负根 C、有一个负根,两个正根 D、有三个正根20. 利用图象解一元二次方程x2-2x-1=0时,我们采用的一种方法是在直角坐标系中画出抛物线y=x2和直线y=2x+1,两图象交点的横坐标就是该方程的解. (1)、请再给出一种利用图象求方程x2-2x-1=0的解的方法;(2)、已知函数y=x3的图象(如图),求方程x3-x-2=0的解(结果保留两位有效数字).21. 二次函数y=ax2+bx+c(a≠0)的图象如图所示.
(1)、请再给出一种利用图象求方程x2-2x-1=0的解的方法;(2)、已知函数y=x3的图象(如图),求方程x3-x-2=0的解(结果保留两位有效数字).21. 二次函数y=ax2+bx+c(a≠0)的图象如图所示. (1)、求方程ax2+bx+c=0的两个根.(2)、当y>0时,求x的取值范围.(3)、当y随着x的增大而减小时,求自变量x的取值范围.(4)、若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.22. 例:利用函数图象求方程x2﹣2x﹣2=0的实数根(结果保留小数点后一位).
(1)、求方程ax2+bx+c=0的两个根.(2)、当y>0时,求x的取值范围.(3)、当y随着x的增大而减小时,求自变量x的取值范围.(4)、若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.22. 例:利用函数图象求方程x2﹣2x﹣2=0的实数根(结果保留小数点后一位).解:画出函数y=x2﹣2x﹣2的图象,它与x轴的公共点的横坐标大约是﹣0.7,2.7.所以方程x2﹣2x﹣2=0的实数根为x1≈﹣0.7,x2≈2.7.我们还可以通过不断缩小根所在的范围估计一元二次方程的根.……这种求根的近似值的方法也适用于更高次的一元方程.

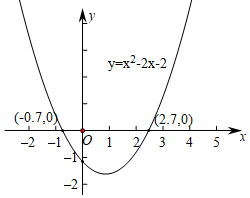
根据你对上面教材内容的阅读与理解,解决下列问题:
(1)、利用函数图象确定不等式x2﹣4x+3<0的解集是;利用函数图象确定方程x2﹣4x+3= 的解是.(2)、为讨论关于x的方程|x2﹣4x+3|=m解的情况,我们可利用函数y=|x2﹣4x+3|的图象进行研究.①请在网格内画出函数y=|x2﹣4x+3|的图象;
②若关于x的方程|x2﹣4x+3|=m有四个不相等的实数解,求m的取值范围;
③若关于x的方程|x2﹣4x+3|=m有四个不相等的实数解x1 , x2 , x3 , x4(x1<x2<x3<x4),满足x4﹣x3=x3﹣x2=x2﹣x1 , 求m的值.
23. 抛物线与x轴交于不重合的两点 , ..(1)、若 , 当时,求抛物线解析式;(2)、若 , 比较c与的大小,并说明理由;(3)、若AB的中点坐标为 , 且 , 设此抛物线顶点为P,交y轴于点D,延长PD交x轴于点E,点O为坐标原点,令面积为S,求S的取值范围.24. 已知二次函数 . (1)、若 ,且函数图象经过 , 两点,求此二次函数的解析式,直接写出抛物线与 轴交点及顶点的坐标;(2)、在图①中画出⑴中函数的大致图象,并根据图象写出函数值 时自变量 的取值范围;(3)、若 且 ,一元二次方程 两根之差等于 ,函数 图象经过 两点,试比较 的大小 .
(1)、若 ,且函数图象经过 , 两点,求此二次函数的解析式,直接写出抛物线与 轴交点及顶点的坐标;(2)、在图①中画出⑴中函数的大致图象,并根据图象写出函数值 时自变量 的取值范围;(3)、若 且 ,一元二次方程 两根之差等于 ,函数 图象经过 两点,试比较 的大小 .