2023年中考数学复习考点一遍过——函数基础知识
试卷更新日期:2022-12-25 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 水中涟漪(圆形水波)不断扩大,记它的半径为r,则圆周长C与r的关系式为 .下列判断正确的是( )A、2是变量 B、 是变量 C、r是变量 D、C是常量2. 函数的自变量x的取值范围是( )A、且 B、且 C、 D、且3. 某城市市区人口万人,市区绿地面积50万平方米,平均每人拥有绿地平方米,则与之间的函数表达式为( )A、 B、 C、 D、4. 点所在象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 甲、乙两人沿同一直道从地到地,在整个行程中,甲、乙离地的距离与时间之间的函数关系如图所示,下列说法错误的是( )
 A、甲比乙早1分钟出发 B、乙的速度是甲的速度的2倍 C、若甲比乙晚5分钟到达,则甲用时10分钟 D、若甲出发时的速度为原来的2倍,则甲比乙提前1分钟到达地6. 如图,正方形的边长为 , 将正方形绕原点O顺时针旋转45°,则点B的对应点的坐标为( )
A、甲比乙早1分钟出发 B、乙的速度是甲的速度的2倍 C、若甲比乙晚5分钟到达,则甲用时10分钟 D、若甲出发时的速度为原来的2倍,则甲比乙提前1分钟到达地6. 如图,正方形的边长为 , 将正方形绕原点O顺时针旋转45°,则点B的对应点的坐标为( )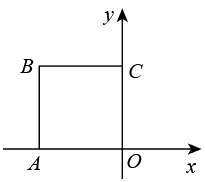 A、 B、 C、 D、7. 已知y1和y2均是以x为自变量的函数,当x=n时,函数值分别是N1和N2 , 若存在实数n,使得N1+N2=1,则称函数y1和y2是“和谐函数”.则下列函数y1和y2不是“和谐函数”的是( )A、y1=x2+2x和y2=﹣x+1 B、y1=和y2=x+1 C、y1=﹣和y2=﹣x﹣1 D、y1=x2+2x和y2=﹣x﹣18. 东东用仪器匀速向如图容器中注水,直到注满为止.用t表示注水时间,y表示水面的高度,下列图象适合表示y与t的对应关系的是( )
A、 B、 C、 D、7. 已知y1和y2均是以x为自变量的函数,当x=n时,函数值分别是N1和N2 , 若存在实数n,使得N1+N2=1,则称函数y1和y2是“和谐函数”.则下列函数y1和y2不是“和谐函数”的是( )A、y1=x2+2x和y2=﹣x+1 B、y1=和y2=x+1 C、y1=﹣和y2=﹣x﹣1 D、y1=x2+2x和y2=﹣x﹣18. 东东用仪器匀速向如图容器中注水,直到注满为止.用t表示注水时间,y表示水面的高度,下列图象适合表示y与t的对应关系的是( )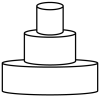 A、
A、 B、
B、 C、
C、 D、
D、 9. 如图是一个教室平面示意图,我们把小刚的座位“第1列第3排”记为 .若小丽的座位为 ,以下四个座位中,与小丽相邻且能比较方便地讨论交流的同学的座位是( )
9. 如图是一个教室平面示意图,我们把小刚的座位“第1列第3排”记为 .若小丽的座位为 ,以下四个座位中,与小丽相邻且能比较方便地讨论交流的同学的座位是( ) A、 B、 C、 D、10. 已知张强家、体育场、文具店在同一直线上.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.图中x表示时间,y表示张强离家的距离.则下列结论不正确的是( )
A、 B、 C、 D、10. 已知张强家、体育场、文具店在同一直线上.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.图中x表示时间,y表示张强离家的距离.则下列结论不正确的是( )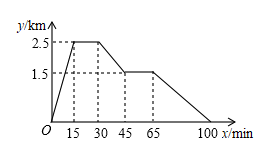 A、张强从家到体育场用了15min B、体育场离文具店1.5km C、张强在文具店停留了20min D、张强从文具店回家用了35min
A、张强从家到体育场用了15min B、体育场离文具店1.5km C、张强在文具店停留了20min D、张强从文具店回家用了35min二、填空题(每空3分,共30分)
-
11. 若式子有意义,则实数x的取值范围是.12. 若点P(m+1,m)在第四象限,则点Q(﹣3,m+2)在第象限.13. 如图,在平面直角坐标系中, 为等腰三角形, ,点B到x轴的距离为4,若将 绕点O逆时针旋转 ,得到 ,则点 的坐标为.
 14. 中国象棋文化历史久远.某校开展了以“纵横之间有智意 攻防转换有乐趣”为主题的中国象棋文化节,如图所示是某次对弈的残局图,如果建立平面直角坐标系,使“帥”位于点(﹣1,﹣2),“馬”位于点(2,﹣2),那么“兵”在同一坐标系下的坐标是.
14. 中国象棋文化历史久远.某校开展了以“纵横之间有智意 攻防转换有乐趣”为主题的中国象棋文化节,如图所示是某次对弈的残局图,如果建立平面直角坐标系,使“帥”位于点(﹣1,﹣2),“馬”位于点(2,﹣2),那么“兵”在同一坐标系下的坐标是.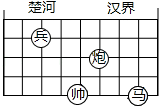 15. 如图,在平面直角坐标系中,把一个点从原点开始向上平移1个单位,再向右平移1个单位,得到点;把点向上平移2个单位,再向左平移2个单位,得到点;把点向下平移3个单位,再向左平移3个单位,得到点;把点向下平移4个单位,再向右平移4个单位,得到点;…;按此做法进行下去,则点的坐标为.
15. 如图,在平面直角坐标系中,把一个点从原点开始向上平移1个单位,再向右平移1个单位,得到点;把点向上平移2个单位,再向左平移2个单位,得到点;把点向下平移3个单位,再向左平移3个单位,得到点;把点向下平移4个单位,再向右平移4个单位,得到点;…;按此做法进行下去,则点的坐标为. 16. 三个能够重合的正六边形的位置如图.已知B点的坐标是(﹣ ,3),则A点的坐标是
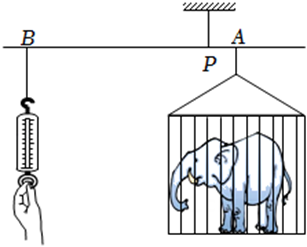
16. 三个能够重合的正六边形的位置如图.已知B点的坐标是(﹣ ,3),则A点的坐标是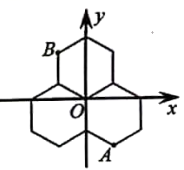 17. 函数的自变量的取值范围是.18. 某动物园利用杠杆原理称象;如图,在点P处挂一根质地均匀且足够长的钢梁(呈水平状态),将装有大象的铁笼和弹簧秤(秤的重力忽略不许)分别悬挂在钢梁的点A、B处,当钢梁保持水平时,弹簧秤读数为k(N),若铁笼固定不动,移动弹簧秤使BP扩大到原来的n(n>1)倍,且钢梁保持水平,则弹簧秤读数为(N)(用含n,k的代数式表示)
17. 函数的自变量的取值范围是.18. 某动物园利用杠杆原理称象;如图,在点P处挂一根质地均匀且足够长的钢梁(呈水平状态),将装有大象的铁笼和弹簧秤(秤的重力忽略不许)分别悬挂在钢梁的点A、B处,当钢梁保持水平时,弹簧秤读数为k(N),若铁笼固定不动,移动弹簧秤使BP扩大到原来的n(n>1)倍,且钢梁保持水平,则弹簧秤读数为(N)(用含n,k的代数式表示)
 19. 如图1,在△ABC中,∠B=36°,动点P从点A出发,沿折线A→B→C匀速运动至点C停止.若点P的运动速度为1cm/s,设点P的运动时间为t(s),AP的长度为y(cm),y与t的函数图象如图2所示.当AP恰好平分∠BAC时,t的值为.
19. 如图1,在△ABC中,∠B=36°,动点P从点A出发,沿折线A→B→C匀速运动至点C停止.若点P的运动速度为1cm/s,设点P的运动时间为t(s),AP的长度为y(cm),y与t的函数图象如图2所示.当AP恰好平分∠BAC时,t的值为.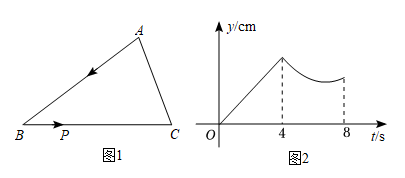 20. 一个装有进水管和出水管的容器,开始时,先打开进水管注水,3分钟时,再打开出水管排水,8分钟时,关闭进水管,直至容器中的水全部排完.在整个过程中,容器中的水量y(升)与时间x(分钟)之间的函数关系如图所示,则图中a的值为.
20. 一个装有进水管和出水管的容器,开始时,先打开进水管注水,3分钟时,再打开出水管排水,8分钟时,关闭进水管,直至容器中的水全部排完.在整个过程中,容器中的水量y(升)与时间x(分钟)之间的函数关系如图所示,则图中a的值为.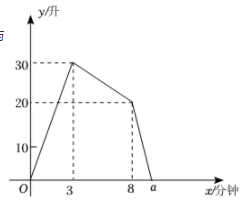
三、综合题(共6题,共60分)
-
21. 已知A、B两地之间有一条长440千米的高速公路.甲、乙两车分别从A、B两地同时出发,沿此公路相向而行,甲车先以100千米/时的速度匀速行驶200千米后与乙车相遇,再以另一速度继续匀速行驶4小时到达B地;乙车匀速行驶至A地,两车到达各自的目的地后停止.两车距A地的路程y(千米)与各自的行驶时间x(时)之间的函数关系如图所示.
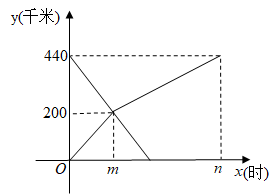 (1)、m= , n=;(2)、求两车相遇后,甲车距A地的路程y与x之间的函数关系式;(3)、当乙车到达A地时,求甲车距A地的路程.22. 某超市销售一种进价为18元/千克的商品,经市场调查后发现,每天的销售量y(千克)与销售单价x(元/千克)有如下表所示的关系:
(1)、m= , n=;(2)、求两车相遇后,甲车距A地的路程y与x之间的函数关系式;(3)、当乙车到达A地时,求甲车距A地的路程.22. 某超市销售一种进价为18元/千克的商品,经市场调查后发现,每天的销售量y(千克)与销售单价x(元/千克)有如下表所示的关系:销售单价x(元/千克)
…
20
22.5
25
37.5
40
…
销售量y(千克)
…
30
27.5
25
12.5
10
…
 (1)、根据表中的数据在下图中描点 , 并用平滑曲线连接这些点,请用所学知识求出y关于x的函数关系式;(2)、设该超市每天销售这种商品的利润为w(元)(不计其它成本),
(1)、根据表中的数据在下图中描点 , 并用平滑曲线连接这些点,请用所学知识求出y关于x的函数关系式;(2)、设该超市每天销售这种商品的利润为w(元)(不计其它成本),①求出w关于x的函数关系式,并求出获得最大利润时,销售单价为多少;
②超市本着“尽量让顾客享受实惠”的销售原则,求(元)时的销售单价.
23. 如图,点在射线上,.如果绕点按逆时针方向旋转到 , 那么点的位置可以用表示.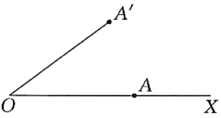 (1)、按上述表示方法,若 , , 则点的位置可以表示为;(2)、在(1)的条件下,已知点的位置用表示,连接、.求证:.24. 在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.
(1)、按上述表示方法,若 , , 则点的位置可以表示为;(2)、在(1)的条件下,已知点的位置用表示,连接、.求证:.24. 在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.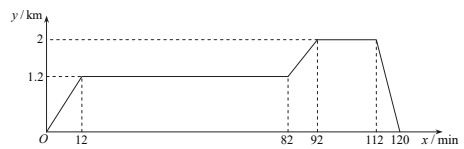
已知学生公寓、阅览室、超市依次在同一条直线上,阅览室离学生公寓 , 超市离学生公寓 , 小琪从学生公寓出发,匀速步行了到阅览室;在阅览室停留后,匀速步行了到超市;在超市停留后,匀速骑行了返回学生公寓.给出的图象反映了这个过程中小琪离学生公寓的距离与离开学生公寓的时间之间的对应关系.
请根据相关信息,解答下列问题:
(1)、填表:离开学生公寓的时间/
5
8
50
87
112
离学生公寓的距离/
0.5
1.6
(2)、填空:①阅览室到超市的距离为;
②小琪从超市返回学生公寓的速度为;
③当小琪离学生公寓的距离为时,他离开学生公寓的时间为 .
(3)、当时,请直接写出y关于x的函数解析式.25. 如图,是一个“函数求值机”的示意图,其中y是x的函数.下面表格中,是通过该“函数求值机”得到的几组x与y的对应值.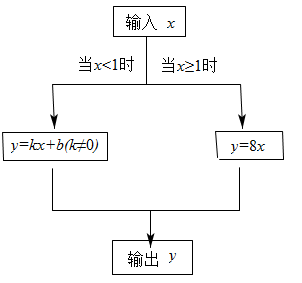
输人x
…
-6
-4
-2
0
2
…
输出y
…
-6
-2
2
6
16
…
根据以上信息,解答下列问题:
(1)、当输入的x值为1时,输出的y值为;(2)、求k,b的值;(3)、当输出的y值为0时,求输入的x值.26. 6月13日,某港口的湖水高度y(cm)和时间x(h)的部分数据及函数图象如下:x(h)
…
11
12
13
14
15
16
17
18
…
Y(cm
…
189
137
103
80
101
133
202
260
…
(数据来自某海洋研究所)
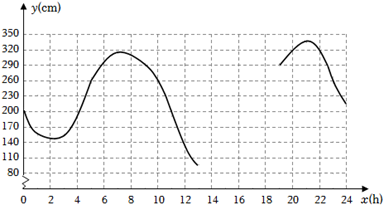 (1)、数学活动:
(1)、数学活动:①根据表中数据,通过描点、连线(光滑曲线)的方式补全该函数的图象.
②观察函数图象,当x=4时,y的值为多少?当y的值最大时,x的值为多少?
(2)、数学思考:请结合函数图象,写出该函数的两条性质或结论.
(3)、数学应用:根据研究,当潮水高度超过260cm时,货轮能够安全进出该港口.请问当天什么时间段适合货轮进出此港口?