浙教版备考2023年中考数学一轮复习39.二次函数及其图象与性质
试卷更新日期:2022-12-25 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 已知函数是二次函数,则m的取值范围为( )A、 B、 C、 D、任意实数2. 已知抛物线的开口向上,那么a的取值可以是( )A、-2 B、-1 C、0 D、23. 对于抛物线 , 下列判断正确的是( )A、顶点 B、抛物线向左平移个单位长度后得到 C、抛物线与y轴的交点是 D、当时,y随x的增大而增大4. 已知二次函数(a,b为常数),命题①:该函数的图象经过点(1,0);命题②:该函数的图象经过点(3,0);命题③:该函数的图象与x轴的交点位于y轴的两侧;命题④:该函数的图象的对称轴为直线x=1.如果这四个命题中只有一个命题是假命题,则这个假命题是( )A、命题① B、命题② C、命题③ D、命题④5. 二次函数y=-x2+2x+n图象的顶点坐标是(m,1),则m-n的值为( )A、1 B、0 C、1 D、26. 关于函数下列说法正确的是( )A、无论m取何值,函数图象总经过点(1,0)和(-1,-2) B、当时,函数图象与x轴总有2个交点 C、若 , 则当x<1时,y随x的增大而减小 D、若m>0时,函数有最小值是7. 已知二次函数 (其中m>0),下列说法正确的是( )A、当x>2时,都有y随着x的增大而增大 B、当x<3时,都有y随着x的增大而减小 C、若x<n时,都有y随着x的增大而减小,则 D、若x<n时,都有y随着x的增大而减小,则8. 抛物线与坐标轴的交点个数为( )A、无交点 B、1个 C、2个 D、3个9. 已知,二次函数y=ax2+bx-1(a,b是常数,a≠0)的图象经过A(2,1),B(4,3),C(4,-1)三个点中的其中两个点,平移该函数的图象,使其顶点始终在直线y=x-1上,则平移后所得抛物线与y轴交点纵坐标的( )A、最大值为-1 B、最小值为-1 C、最大值为 D、最小值为10. 如图,在平面直角坐标系中,矩形ABCD的顶点A、C的坐标分别为(-4,1),(-1,-4),且AD平行于x轴,当函数y=x2+2mx-2(x≤0)的图象在矩形ABCD内部的部分均为y随x的增大而减小时,下列选项中符合条件的m的取值范围为( )
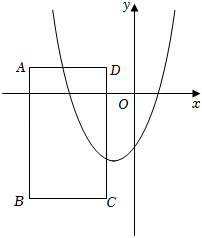 A、1≤m≤ B、0≤m≤ C、-1<m≤1或≤m< D、-1<m≤0或1≤m<
A、1≤m≤ B、0≤m≤ C、-1<m≤1或≤m< D、-1<m≤0或1≤m<二、填空题(每题4分,共24分)
-
11. 下列函数:①;②;③;④ , 其中y的值随x的增大而增大的函数为 . (填序号)12. 若点都在二次函数的图象上,则 , , 的大小关系为 . (用“<”连接)13. 将抛物线先向右平移1个单位长度,再向上平移2个单位长度,得到的抛物线的函数表达式为 .14. 若将二次函数配方为的形式,则y=。15. 如图,抛物线与x轴交于点和点 , 以下结论:
①;②;③;④当时,y随x的增大而减小.其中正确的结论有 . (填写代表正确结论的序号)
 16. 如图,是等边三角形, , 点为边上的动点, , 交于点 , 线段的最大值为 .
16. 如图,是等边三角形, , 点为边上的动点, , 交于点 , 线段的最大值为 .
三、解答题(共8题,共66分)
-
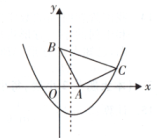
17. 如图,在平面直角坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线y=x2+bx-2过点C.求抛物线的表达式.
 18. 小尧用“描点法”画二次函数的 图像,列表如下:
18. 小尧用“描点法”画二次函数的 图像,列表如下:x
…
-4
-3
-2
-1
0
1
2
…
y
…
5
0
-3
-4
-3
0
-5
…
 (1)、由于粗心,小尧算错了其中的一个 y值,请你指出这个算错的y值所对应的x=;(2)、在图中画出这个二次函数的图像;(3)、当 y≥5 时,x 的取值范围是 .19. 如图,抛物线交x轴于点和 , 交y轴于点C,抛物线的顶点为D.
(1)、由于粗心,小尧算错了其中的一个 y值,请你指出这个算错的y值所对应的x=;(2)、在图中画出这个二次函数的图像;(3)、当 y≥5 时,x 的取值范围是 .19. 如图,抛物线交x轴于点和 , 交y轴于点C,抛物线的顶点为D. (1)、当时,求b的值.(2)、抛物线上有两点和 , 若 , 且 , 比较的大小关系.20. 已知二次函数y=2x2-4x-6.(1)、将y=2x2-4x-6化成y=a(x-h)2+k的形式;(2)、写出抛物线的开口方向、对称轴和顶点坐标.(3)、当-1≤x≤2时,直接写出函数y的取值范围;21. 已知二次函数(a>0)(1)、求二次函数图象的对称轴;(2)、当时,y的最大值与最小值的差为2,求该二次函数的表达式;(3)、对于二次函数图象上的两点 , , 当时,均满足 , 请结合函数图象,求的取值范围。22. 新定义:我们把抛物线(其中)与抛物线称为“关联抛物线”.例如:抛物线的“关联抛物线”为:.已知抛物线的“关联抛物线”为.(1)、写出的解析式(用含a的式子表示)及顶点坐标;(2)、若 , 过x轴上一点P,作x轴的垂线分别交抛物线 , 于点M,N.
(1)、当时,求b的值.(2)、抛物线上有两点和 , 若 , 且 , 比较的大小关系.20. 已知二次函数y=2x2-4x-6.(1)、将y=2x2-4x-6化成y=a(x-h)2+k的形式;(2)、写出抛物线的开口方向、对称轴和顶点坐标.(3)、当-1≤x≤2时,直接写出函数y的取值范围;21. 已知二次函数(a>0)(1)、求二次函数图象的对称轴;(2)、当时,y的最大值与最小值的差为2,求该二次函数的表达式;(3)、对于二次函数图象上的两点 , , 当时,均满足 , 请结合函数图象,求的取值范围。22. 新定义:我们把抛物线(其中)与抛物线称为“关联抛物线”.例如:抛物线的“关联抛物线”为:.已知抛物线的“关联抛物线”为.(1)、写出的解析式(用含a的式子表示)及顶点坐标;(2)、若 , 过x轴上一点P,作x轴的垂线分别交抛物线 , 于点M,N.①当时,求点a的坐标;
②当时,的最大值与最小值的差为 , 求a的值.
23. 如图,二次函数的图像与轴交于、两点,与轴交于点 , 点是二次函数图象上的一对对称点,一次函数的图像过点 . (1)、直接写出点的坐标;(2)、求二次函数的解析式;(3)、将二次函数的图像向左平移2个单位,再向下平移2个单位,写出得到的图象的解析式;(4)、根据图象求中的取值范围.24. 如图,抛物线与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.
(1)、直接写出点的坐标;(2)、求二次函数的解析式;(3)、将二次函数的图像向左平移2个单位,再向下平移2个单位,写出得到的图象的解析式;(4)、根据图象求中的取值范围.24. 如图,抛物线与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.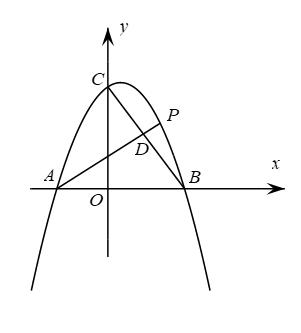 (1)、A,B,C三点的坐标为 , , ;(2)、连接 , 交线段于点D,
(1)、A,B,C三点的坐标为 , , ;(2)、连接 , 交线段于点D,①当与x轴平行时,求的值;
②当与x轴不平行时,求的最大值;
(3)、连接 , 是否存在点P,使得 , 若存在,求m的值,若不存在,请说明理由.