浙教版备考2023年中考数学一轮复习38.反比例函数的应用
试卷更新日期:2022-12-25 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 研究发现,近视镜的度数y(度)与镜片焦距x(米)成反比例函数关系,小明佩戴的400度近视镜片的焦距为0.25米,经过一段时间的矫正治疗加之注意用眼健康,现在镜片焦距为0.4米,则小明的近视镜度数可以调整为( )A、300度 B、500度 C、250度 D、200度2. 地球周围的大气层阻挡了紫外线和宇宙射线对地球生命的伤害,同时产生一定的大气压,海拔不同,大气压不同,观察图中数据,你发现,正确的是( )
 A、海拔越高,大气压越大 B、图中曲线是反比例函数的图象 C、海拔为4千米时,大气压约为70千帕 D、图中曲线表达了大气压和海拔两个量之间的变化关系3. 呼气式酒精测试仪中装有酒精气体传感器,可用于检测驾驶员是否酒后驾车.酒精气体传感器是一种气敏电阻(图1中的 ), 的阻值随呼气酒精浓度K的变化而变化(如图2),血液酒精浓度M与呼气酒精浓度K的关系见图3.下列说法不正确的是( )
A、海拔越高,大气压越大 B、图中曲线是反比例函数的图象 C、海拔为4千米时,大气压约为70千帕 D、图中曲线表达了大气压和海拔两个量之间的变化关系3. 呼气式酒精测试仪中装有酒精气体传感器,可用于检测驾驶员是否酒后驾车.酒精气体传感器是一种气敏电阻(图1中的 ), 的阻值随呼气酒精浓度K的变化而变化(如图2),血液酒精浓度M与呼气酒精浓度K的关系见图3.下列说法不正确的是( ) A、呼气酒精浓度K越大, 的阻值越小 B、当K=0时, 的阻值为100 C、当K=10时,该驾驶员为非酒驾状态 D、当 时,该驾驶员为醉驾状态4. 某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对 ,在坐标系中进行描点,则正确的是()A、
A、呼气酒精浓度K越大, 的阻值越小 B、当K=0时, 的阻值为100 C、当K=10时,该驾驶员为非酒驾状态 D、当 时,该驾驶员为醉驾状态4. 某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对 ,在坐标系中进行描点,则正确的是()A、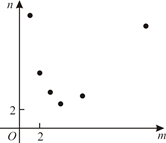 B、
B、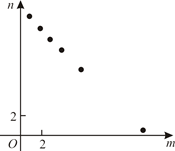 C、
C、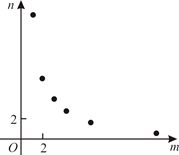 D、
D、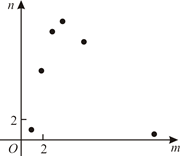 5. 如图,在四边形 中, , , , 平分 .设 , ,则 关于 的函数关系用图象大致可以表示为( )
5. 如图,在四边形 中, , , , 平分 .设 , ,则 关于 的函数关系用图象大致可以表示为( )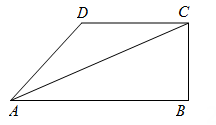 A、
A、 B、
B、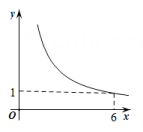 C、
C、 D、
D、 6. 学校的自动饮水机,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降.此时水温(℃)与通电时间成反比例关系.当水温将至20℃时,饮水机再自动加热,若水温在20℃时接通电源,水温y与通电时间x之间的关系如图所示,则下列说法中正确的是( )
6. 学校的自动饮水机,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降.此时水温(℃)与通电时间成反比例关系.当水温将至20℃时,饮水机再自动加热,若水温在20℃时接通电源,水温y与通电时间x之间的关系如图所示,则下列说法中正确的是( ) A、水温从20℃加热到100℃,需要 B、水温下降过程中,y与x的函数关系式是 C、上午8点接通电源,可以保证当天9:30能喝到不超过40℃的水 D、水温不低于30℃的时间为7. 某校科技小组进行野外考察,利用铺垫木板的方式,通过了一片烂泥湿地,他们发现,当人和木板对湿地的压力一定时,人和木板对地面的压强p()随着木板面积S()的变化而变化,如果人和木板对湿地地面的压力合计 , 那么下列说法正确的是( )
A、水温从20℃加热到100℃,需要 B、水温下降过程中,y与x的函数关系式是 C、上午8点接通电源,可以保证当天9:30能喝到不超过40℃的水 D、水温不低于30℃的时间为7. 某校科技小组进行野外考察,利用铺垫木板的方式,通过了一片烂泥湿地,他们发现,当人和木板对湿地的压力一定时,人和木板对地面的压强p()随着木板面积S()的变化而变化,如果人和木板对湿地地面的压力合计 , 那么下列说法正确的是( ) A、p与S的函数表达式为 B、当S越来越大时,p也越来越大 C、若压强不超过时,木板面积最多 D、当木板面积为时,压强是8. 某杠杆装置如图,杆的一端吊起一桶水,阻力臂保持不变在使杠杆平衡的情况下,小康通过改变动力臂L,测量出相应的动力F数据如表.请根据表中数据规律探求,当动力臂L长度为2.0m时,所需动力最接近( )
A、p与S的函数表达式为 B、当S越来越大时,p也越来越大 C、若压强不超过时,木板面积最多 D、当木板面积为时,压强是8. 某杠杆装置如图,杆的一端吊起一桶水,阻力臂保持不变在使杠杆平衡的情况下,小康通过改变动力臂L,测量出相应的动力F数据如表.请根据表中数据规律探求,当动力臂L长度为2.0m时,所需动力最接近( )动力臂L(m)
动力F(N)
0.5
600
1.0
302
1.5
200
2.0
a
2.5
120
 A、120N B、151N C、300N D、302N9. 已知蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.若此蓄电池为某用电器的电源,限制电流不能超过12A,那么用电器的可变电阻R应控制在什么范围?( )
A、120N B、151N C、300N D、302N9. 已知蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.若此蓄电池为某用电器的电源,限制电流不能超过12A,那么用电器的可变电阻R应控制在什么范围?( )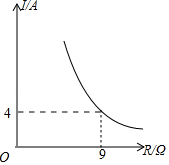 A、R≥3Ω B、R≤3Ω C、R≥12Ω D、R≥24Ω10. 某品牌的饮水机接通电源就进入自动程序:开机加热到水温100℃,停止加热,水温开始下降,此时水温y(℃)与开机后用时.x(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,水温从100℃降到35℃所用的时间是( )
A、R≥3Ω B、R≤3Ω C、R≥12Ω D、R≥24Ω10. 某品牌的饮水机接通电源就进入自动程序:开机加热到水温100℃,停止加热,水温开始下降,此时水温y(℃)与开机后用时.x(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,水温从100℃降到35℃所用的时间是( )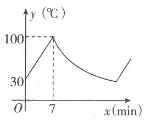 A、27min B、20min C、13min D、7min
A、27min B、20min C、13min D、7min二、填空题(每题4分,共24分)
-
11. 举出一个生活中应用反比例函数的例子: .12. 根据物理学知识,在压力不变的情况下,某物体承受的压强是它的受力面积的反比例函数,其函数图象如图所示,当时,该物体承受的压强p的值为 Pa.
 13. 列车从甲地驶往乙地.行完全程所需的时间与行驶的平均速度之间的反比例函数关系如图所示.若列车要在内到达,则速度至少需要提高到 .
13. 列车从甲地驶往乙地.行完全程所需的时间与行驶的平均速度之间的反比例函数关系如图所示.若列车要在内到达,则速度至少需要提高到 . 14. 一个用电器的电阻是可调节的,其调节范围为:110~220Ω.已知电压为220ᴠ,这个用电器的功率P的范围是: w.(P表示功率,R表示电阻,U表示电压,三者关系式为:P·R=U²)15. 矩形的面积为2,一条边的长为x,另一条边的长为y,则用x表示y的函数解析式为(其中x>0)16. 山西拉面,又叫甩面、扯面、抻面,是西北城乡独具地方风味的面食名吃,为山西四大面食之一.将一定体积的面团做成拉面,面条的总长度 与粗细(横截面面积) 之间的变化关系如图所示(双曲线的一支).如果将这个面团做成粗为 的拉面,则做出来的面条的长度为 .
14. 一个用电器的电阻是可调节的,其调节范围为:110~220Ω.已知电压为220ᴠ,这个用电器的功率P的范围是: w.(P表示功率,R表示电阻,U表示电压,三者关系式为:P·R=U²)15. 矩形的面积为2,一条边的长为x,另一条边的长为y,则用x表示y的函数解析式为(其中x>0)16. 山西拉面,又叫甩面、扯面、抻面,是西北城乡独具地方风味的面食名吃,为山西四大面食之一.将一定体积的面团做成拉面,面条的总长度 与粗细(横截面面积) 之间的变化关系如图所示(双曲线的一支).如果将这个面团做成粗为 的拉面,则做出来的面条的长度为 .
三、解答题(共8题,共66分)
-
17. 如图,一块砖的A,B,C三个面的面积比是.如果B面向下放在地上,地面所受压强为 , 那么A面和C面分别向下放在地上时,地面所受压强各是多少?
 18. 为加强生态文明建设,某市环保局对一企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AC表示前3天的变化规律,第3天时硫化物的浓度降为4.5mg/L.从第3天起,所排污水中硫化物的浓度y与时间x满足下面表格中的关系:
18. 为加强生态文明建设,某市环保局对一企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AC表示前3天的变化规律,第3天时硫化物的浓度降为4.5mg/L.从第3天起,所排污水中硫化物的浓度y与时间x满足下面表格中的关系:时间x(天)
3
5
6
9
……
硫化物的浓度y(mg/L)
4.5
2.7
2.25
1.5
……
 (1)、在整改过程中,当0≤x<3时,硫化物的浓度y与时间x的函数表达式;(2)、在整改过程中,当x≥3时,硫化物的浓度y与时间x的函数表达式;(3)、该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L?为什么?19. 某燃气公司计划在地下修建一个容积为V(V为定值,单位:m3)的圆柱形天然气储存室,储存室的底面积S(单位:m2) 与其深度d(单位:m)是反比例函数关系,它的图象如图所示.
(1)、在整改过程中,当0≤x<3时,硫化物的浓度y与时间x的函数表达式;(2)、在整改过程中,当x≥3时,硫化物的浓度y与时间x的函数表达式;(3)、该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L?为什么?19. 某燃气公司计划在地下修建一个容积为V(V为定值,单位:m3)的圆柱形天然气储存室,储存室的底面积S(单位:m2) 与其深度d(单位:m)是反比例函数关系,它的图象如图所示.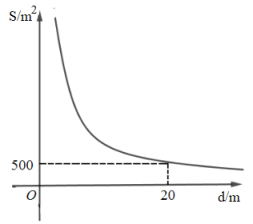 (1)、求储存室的容积V的值;(2)、受地形条件限制,储存室的深度d需要满足16≤d≤25,求储存室的底面积S的取值范围.20. 如图,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高 y (单位:cm)是物距(小孔到蜡烛的距离)x(单位:cm)的反比例函数,当x=6时,y=2.
(1)、求储存室的容积V的值;(2)、受地形条件限制,储存室的深度d需要满足16≤d≤25,求储存室的底面积S的取值范围.20. 如图,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高 y (单位:cm)是物距(小孔到蜡烛的距离)x(单位:cm)的反比例函数,当x=6时,y=2. (1)、求y关于x的函数解析式;(2)、若火焰的像高为 3cm ,求小孔到蜡烛的距离.21. 市政府计划建设一项水利工程,工程需要运送的土石方总量为106立方米,某运输公司承担了运送土石方的任务.设该公司平均每天运送土石方总量为y立方米,完成运送任务所需时间为t天.(1)、求y关于t的函数表达式;(2)、当y=1000时,求t的值;(3)、若工期要求在100天内完成,公司每天至少要运送多少立方米土石方?22. 如图所示,制作一种产品的同时,需要将原材料加热,设该材料温度为 , 从加热开始计算的时间为分钟,据了解,该材料在加热过程中温度与时间成一次函数关系,已知该材料在加热前的温度为 , 加热5分钟使材料温度达到时停止加热.停止加热后,过一段时间,材料温度逐渐下降,这时温度与时间成反比例函数关系.
(1)、求y关于x的函数解析式;(2)、若火焰的像高为 3cm ,求小孔到蜡烛的距离.21. 市政府计划建设一项水利工程,工程需要运送的土石方总量为106立方米,某运输公司承担了运送土石方的任务.设该公司平均每天运送土石方总量为y立方米,完成运送任务所需时间为t天.(1)、求y关于t的函数表达式;(2)、当y=1000时,求t的值;(3)、若工期要求在100天内完成,公司每天至少要运送多少立方米土石方?22. 如图所示,制作一种产品的同时,需要将原材料加热,设该材料温度为 , 从加热开始计算的时间为分钟,据了解,该材料在加热过程中温度与时间成一次函数关系,已知该材料在加热前的温度为 , 加热5分钟使材料温度达到时停止加热.停止加热后,过一段时间,材料温度逐渐下降,这时温度与时间成反比例函数关系.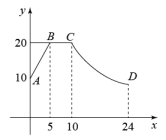 (1)、分别求出该材料加热过程中和材料温度逐渐下降过程中,与之间的函数表达式,并写出的取值范围;(2)、根据工艺要求,在材料温度不低于的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理所用的时间是多少?23. 某小组进行漂洗实验,每次漂洗的衣服量和添加洗衣粉量固定不变实验发现,当每次漂洗用水量v(升)一定时,衣服中残留的洗衣粉量y(克)与漂洗次数x(次)满足y=(k为常数),已知当使用5升水,漂洗1次后,衣服中残留洗衣粉2克.(1)、求k的值.(2)、如果每次用水5升,要求漂洗后残留的洗衣粉量小于0.8克,求至少漂洗多少次?(3)、现将20升水等分成x次(x>1)漂洗,要使残留的洗衣粉量降到0.5克,求每次漂洗用水多少升?24. 如图1为北京冬奥会“雪飞天”滑雪大跳台赛道的横截面示意图.取水平线OE为x轴,铅垂线OD为y轴,建立平面直角坐标系.运动员以速度从D点滑出,运动轨迹近似抛物线 . 某运动员7次试跳的轨迹如图2.在着陆坡CE上设置点K(与DO相距32m)作为标准点,着陆点在K点或超过K点视为成绩达标.
(1)、分别求出该材料加热过程中和材料温度逐渐下降过程中,与之间的函数表达式,并写出的取值范围;(2)、根据工艺要求,在材料温度不低于的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理所用的时间是多少?23. 某小组进行漂洗实验,每次漂洗的衣服量和添加洗衣粉量固定不变实验发现,当每次漂洗用水量v(升)一定时,衣服中残留的洗衣粉量y(克)与漂洗次数x(次)满足y=(k为常数),已知当使用5升水,漂洗1次后,衣服中残留洗衣粉2克.(1)、求k的值.(2)、如果每次用水5升,要求漂洗后残留的洗衣粉量小于0.8克,求至少漂洗多少次?(3)、现将20升水等分成x次(x>1)漂洗,要使残留的洗衣粉量降到0.5克,求每次漂洗用水多少升?24. 如图1为北京冬奥会“雪飞天”滑雪大跳台赛道的横截面示意图.取水平线OE为x轴,铅垂线OD为y轴,建立平面直角坐标系.运动员以速度从D点滑出,运动轨迹近似抛物线 . 某运动员7次试跳的轨迹如图2.在着陆坡CE上设置点K(与DO相距32m)作为标准点,着陆点在K点或超过K点视为成绩达标.(参考数据: , )
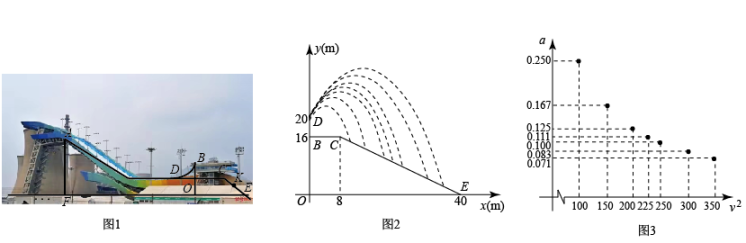 (1)、求线段CE的函数表达式(写出的取值范围).(2)、当时,着陆点为P,求P的横坐标并判断成绩是否达标.(3)、在试跳中发现运动轨迹与滑出速度v的大小有关,进一步探究,测算得7组a与 的对应数据,在平面直角坐标系中描点如图3.
(1)、求线段CE的函数表达式(写出的取值范围).(2)、当时,着陆点为P,求P的横坐标并判断成绩是否达标.(3)、在试跳中发现运动轨迹与滑出速度v的大小有关,进一步探究,测算得7组a与 的对应数据,在平面直角坐标系中描点如图3.①猜想a关于的函数类型,求函数表达式,并任选一对对应值验证.
②当v为多少m/s时,运动员的成绩恰能达标(精确到1m/s)?