浙教版备考2023年中考数学一轮复习35.一次函数的应用
试卷更新日期:2022-12-25 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 图1是我国青海湖最深处的某一截面图,青海湖水面下任意一点A的压强p(单位:cmHg)与其离水面的深度h(单位:m)的函数解析式为 , 其图象如图2所示,其中为青海湖水面大气压强,k为常数且.根据图中信息分析(结果保留一位小数),下列结论正确的是( )
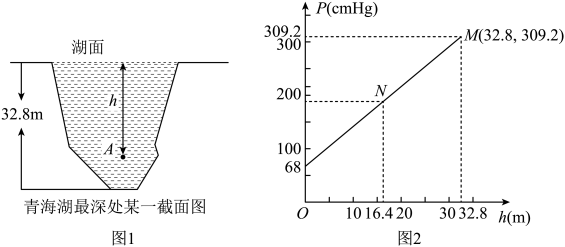 A、青海湖水深16.4m处的压强为188.6cmHg B、青海湖水面大气压强为76.0cmHg C、函数解析式中自变量h的取值范围是 D、P与h的函数解析式为2. 一辆汽车油箱中剩余的油量与已行驶的路程的对应关系如图所示,如果这辆汽车每千米的耗油量相同,当油箱中剩余的油量为时,那么该汽车已行驶的路程为( )
A、青海湖水深16.4m处的压强为188.6cmHg B、青海湖水面大气压强为76.0cmHg C、函数解析式中自变量h的取值范围是 D、P与h的函数解析式为2. 一辆汽车油箱中剩余的油量与已行驶的路程的对应关系如图所示,如果这辆汽车每千米的耗油量相同,当油箱中剩余的油量为时,那么该汽车已行驶的路程为( ) A、 B、 C、 D、3. 小王同学从家出发,步行到离家a米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:米)与出发时间x(单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )
A、 B、 C、 D、3. 小王同学从家出发,步行到离家a米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:米)与出发时间x(单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )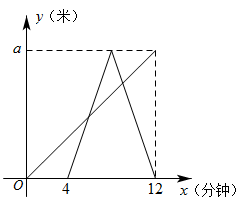 A、2.7分钟 B、2.8分钟 C、3分钟 D、3.2分钟4. 已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )
A、2.7分钟 B、2.8分钟 C、3分钟 D、3.2分钟4. 已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )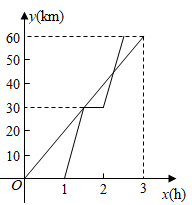 A、15km B、16km C、44km D、45km5. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返同,且往返速度的大小不变,两车离甲地的距离 (单位: )与慢车行驶时间 (单位: )的函数关系如图,则两车先后两次相遇的间隔时间是( )
A、15km B、16km C、44km D、45km5. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返同,且往返速度的大小不变,两车离甲地的距离 (单位: )与慢车行驶时间 (单位: )的函数关系如图,则两车先后两次相遇的间隔时间是( )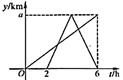 A、 B、 C、 D、6. 鄂尔多斯动物园内的一段线路如图1所示,动物园内有免费的班车,从入口处出发,沿该线路开往大象馆,途中停靠花鸟馆(上下车时间忽略不计),第一班车上午9:20发车,以后每隔10分钟有一班车从入口处发车,且每一班车速度均相同.小聪周末到动物园游玩,上午9点到达入口处,因还没到班车发车时间,于是从入口处出发,沿该线路步行25分钟后到达花鸟馆,离入口处的路程y(米)与时间x(分)的函数关系如图2所示,下列结论错误的是( )
A、 B、 C、 D、6. 鄂尔多斯动物园内的一段线路如图1所示,动物园内有免费的班车,从入口处出发,沿该线路开往大象馆,途中停靠花鸟馆(上下车时间忽略不计),第一班车上午9:20发车,以后每隔10分钟有一班车从入口处发车,且每一班车速度均相同.小聪周末到动物园游玩,上午9点到达入口处,因还没到班车发车时间,于是从入口处出发,沿该线路步行25分钟后到达花鸟馆,离入口处的路程y(米)与时间x(分)的函数关系如图2所示,下列结论错误的是( )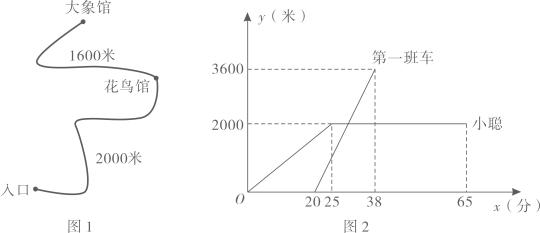 A、第一班车离入口处的距离y(米)与时间x(分)的解析式为y=200x﹣4000(20≤x≤38) B、第一班车从入口处到达花鸟馆所需的时间为10分钟 C、小聪在花鸟馆游玩40分钟后,想坐班车到大象馆,则小聪最早能够坐上第四班车 D、小聪在花鸟馆游玩40分钟后,如果坐第五班车到大象馆,那么比他在花鸟馆游玩结束后立即步行到大象馆提前了7分钟(假设小聪步行速度不变)7. 甲、乙是由两组一模一样的三个圆柱组合而成的容器,现匀速地向两容器注水至满,在注水过程中,甲、乙两容器水面高度h随时间t的变化规律如图所示,则实线对应的容器的形状和A点的坐标分别是( )
A、第一班车离入口处的距离y(米)与时间x(分)的解析式为y=200x﹣4000(20≤x≤38) B、第一班车从入口处到达花鸟馆所需的时间为10分钟 C、小聪在花鸟馆游玩40分钟后,想坐班车到大象馆,则小聪最早能够坐上第四班车 D、小聪在花鸟馆游玩40分钟后,如果坐第五班车到大象馆,那么比他在花鸟馆游玩结束后立即步行到大象馆提前了7分钟(假设小聪步行速度不变)7. 甲、乙是由两组一模一样的三个圆柱组合而成的容器,现匀速地向两容器注水至满,在注水过程中,甲、乙两容器水面高度h随时间t的变化规律如图所示,则实线对应的容器的形状和A点的坐标分别是( ) A、甲,( , 3) B、甲,( , ) C、乙,( , 3) D、乙,( , )8. 甲、乙两名同学在一段2000m长的笔直公路上进行自行车比赛,开始时甲在起点,乙在甲的前方200m处,他们同时同向出发匀速前进,甲的速度是8m/s,乙的速度是6m/s,先到达终点者在终点处等待.设甲、乙两人之间的距离是y(m),比赛时间是x(s),整个过程中y与x之间的函数关系的图象大致是( )A、
A、甲,( , 3) B、甲,( , ) C、乙,( , 3) D、乙,( , )8. 甲、乙两名同学在一段2000m长的笔直公路上进行自行车比赛,开始时甲在起点,乙在甲的前方200m处,他们同时同向出发匀速前进,甲的速度是8m/s,乙的速度是6m/s,先到达终点者在终点处等待.设甲、乙两人之间的距离是y(m),比赛时间是x(s),整个过程中y与x之间的函数关系的图象大致是( )A、 B、
B、 C、
C、 D、
D、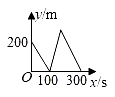 9. 大明因急事在运行中的自动扶梯上行走去二楼,图1中线段OA、OB分别大致表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时,距自动扶梯起点的距离与时间之间的系.下面四个图中,虚线OC能大致表示大明在停止运行(即静止)的自动扶梯上行走去二楼时,距自动扶梯起点的距离与时间关系的是( )
9. 大明因急事在运行中的自动扶梯上行走去二楼,图1中线段OA、OB分别大致表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时,距自动扶梯起点的距离与时间之间的系.下面四个图中,虚线OC能大致表示大明在停止运行(即静止)的自动扶梯上行走去二楼时,距自动扶梯起点的距离与时间关系的是( ) A、
A、 B、
B、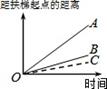 C、
C、 D、
D、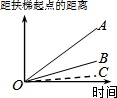 10. 14:00时,时钟中时针与分针的位置如图所示(分针在射线OA上),设经过xmin(0≤x≤30),时针、分针与射线OA所成角的度数分别为y1°、y2°,则y1、y2与x之间的函数关系图是 ( )
10. 14:00时,时钟中时针与分针的位置如图所示(分针在射线OA上),设经过xmin(0≤x≤30),时针、分针与射线OA所成角的度数分别为y1°、y2°,则y1、y2与x之间的函数关系图是 ( ) A、
A、 B、
B、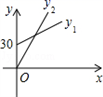 C、
C、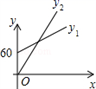 D、
D、
二、填空题(每题3分,共18分)
-
11. 下表中记录了一次试验中时间和温度的数据.
时间/分钟
0
5
10
15
20
25
温度/℃
10
25
40
55
70
85
若温度的变化是均匀的,则14分钟时的温度是℃.
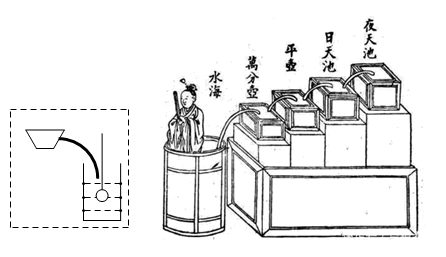
12. 漏刻是我国古代的一种计时工具.据史书记载,西周时期就已经出现了漏刻,这是中国古代入民对函数思想的创造性应用.小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现水位 是时间 的一次函数,下表是小明记录的部分数据,其中有一个 的值记录不符合题意 , 请排除后利用正确的数据确定当 为 时,对应的时间 为min.…
1
2
3
5
…
…
2.4
2.8
3.4
4
…
 13. 育红学校七年级学生步行到郊外旅行.七(1)班出发1h后,七(2)班才出发,同时七(2)班派一名联络员骑自行车在两班队伍之间进行联络,联络员和七(1)班的距离s(km)与七(2)班行进时间t(h)的函数关系图象如图所示.若已知联络员用了 第一次返回到自己班级,则七(2)班需要 h才能追上七(1)班.
13. 育红学校七年级学生步行到郊外旅行.七(1)班出发1h后,七(2)班才出发,同时七(2)班派一名联络员骑自行车在两班队伍之间进行联络,联络员和七(1)班的距离s(km)与七(2)班行进时间t(h)的函数关系图象如图所示.若已知联络员用了 第一次返回到自己班级,则七(2)班需要 h才能追上七(1)班.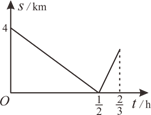 14. 小明从家步行到学校需走的路程为1800米.图中的折线OAB反映了小明从家步行到学校所走的路程s(米)与时间t(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行米.
14. 小明从家步行到学校需走的路程为1800米.图中的折线OAB反映了小明从家步行到学校所走的路程s(米)与时间t(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行米.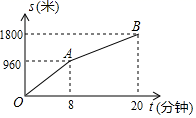 15. A、B两地相距20km,甲乙两人沿同一条路线从A地到B地,甲先出发,匀速行驶,甲出发1小时后乙再出发,乙以2km/h的速度匀速行驶1小时后提高速度并继续匀速行驶,结果比甲提前到达甲、乙两人离开A地的距离y(km)与时间t(h)的关系如图所示,则乙出发小时后和甲相遇.
15. A、B两地相距20km,甲乙两人沿同一条路线从A地到B地,甲先出发,匀速行驶,甲出发1小时后乙再出发,乙以2km/h的速度匀速行驶1小时后提高速度并继续匀速行驶,结果比甲提前到达甲、乙两人离开A地的距离y(km)与时间t(h)的关系如图所示,则乙出发小时后和甲相遇. 16. 一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表,现有15升食物需要存放且要求每个盒子要装满.由于A型号盒子正在做促销活动:购买三个及三个以上可一次性返现金4元,则购买盒子所需要最少费用为元.
16. 一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表,现有15升食物需要存放且要求每个盒子要装满.由于A型号盒子正在做促销活动:购买三个及三个以上可一次性返现金4元,则购买盒子所需要最少费用为元.型号
A
B
单个盒子容量(升)
2
3
单价(元)
5
6
三、解答题(共8题,共72分)
-
17. 在“美丽中国,清洁乡村”活动中,李家村提出两种购买垃圾桶方案:方案1:不分类垃圾桶免费赠送,以后每月的垃圾处理费用800元:方案2:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用200元;设方案1的总费用为y1元,方案2的总费用为y2元,交费时间为x个月.
 (1)、分别写出y1 , y2与x的函数关系式(2)、在同一坐标系内,画出函数y1 , y2的图象;(3)、在不考虑垃圾桶使用寿命的情况下,哪种方案省钱?18. △ABC的周长为12,AC=2AB,设AB=x,BC=y.(1)、求y关于x的函数表达式,并写出自变量x的取值范围;(2)、若△ABC是等腰三角形,求它的三边长.19. 某水果店购进甲、乙两种苹果的进价分别为8元/、12元/ , 这两种苹果的销售额y(单位:元)与销售量x(单位:)之间的关系如图所示.
(1)、分别写出y1 , y2与x的函数关系式(2)、在同一坐标系内,画出函数y1 , y2的图象;(3)、在不考虑垃圾桶使用寿命的情况下,哪种方案省钱?18. △ABC的周长为12,AC=2AB,设AB=x,BC=y.(1)、求y关于x的函数表达式,并写出自变量x的取值范围;(2)、若△ABC是等腰三角形,求它的三边长.19. 某水果店购进甲、乙两种苹果的进价分别为8元/、12元/ , 这两种苹果的销售额y(单位:元)与销售量x(单位:)之间的关系如图所示.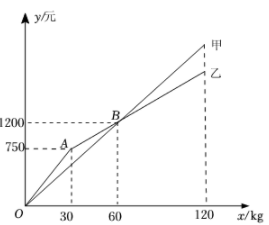 (1)、写出图中点B表示的实际意义;(2)、分别求甲、乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式,并写出x的取值范围;(3)、若不计损耗等因素,当甲、乙两种苹果的销售量均为时,它们的利润和为1500元.求a的值.20. 为落实“双减”政策,丰富课后服务的内容,某学校计划到甲、乙两个体育专卖店购买一批新的体育用品,两个商店的优惠活动如下:
(1)、写出图中点B表示的实际意义;(2)、分别求甲、乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式,并写出x的取值范围;(3)、若不计损耗等因素,当甲、乙两种苹果的销售量均为时,它们的利润和为1500元.求a的值.20. 为落实“双减”政策,丰富课后服务的内容,某学校计划到甲、乙两个体育专卖店购买一批新的体育用品,两个商店的优惠活动如下:甲:所有商品按原价8.5折出售;
乙:一次购买商品总额不超过300元的按原价付费,超过300元的部分打7折.
设需要购买体育用品的原价总额为元,去甲商店购买实付元,去乙商店购买实付元,其函数图象如图所示.
 (1)、分别求 , 关于的函数关系式;(2)、两图象交于点 , 求点坐标;(3)、请根据函数图象,直接写出选择去哪个体育专卖店购买体育用品更合算.21. 由于精准扶贫的措施科学得当,贫困户小颖家今年种植的草莓喜获丰收,采摘上市16天全部销售完.小颖对销售情况进行统计后发现,在该草莓上市第x天(x取整数)时,日销售量y(单位:千克)与x之间的函数关系式为草莓价格m(单位:元/千克)与x之间的函数关系如图所示.
(1)、分别求 , 关于的函数关系式;(2)、两图象交于点 , 求点坐标;(3)、请根据函数图象,直接写出选择去哪个体育专卖店购买体育用品更合算.21. 由于精准扶贫的措施科学得当,贫困户小颖家今年种植的草莓喜获丰收,采摘上市16天全部销售完.小颖对销售情况进行统计后发现,在该草莓上市第x天(x取整数)时,日销售量y(单位:千克)与x之间的函数关系式为草莓价格m(单位:元/千克)与x之间的函数关系如图所示. (1)、求第14天小颖家草莓的日销售量;(2)、求当时,草莓价格m与x之间的函数关系式;(3)、试比较第8天与第10天的销售金额哪天多?22. 小王准备把牛奶加热后饮用,他先在锅中加水,再从冰箱冷藏室中拿出一杯牛奶浸入水中,用煤气灶缓慢加热.在这个过程中,他每隔测量一次水温和牛奶温度,获得数据如下表:
(1)、求第14天小颖家草莓的日销售量;(2)、求当时,草莓价格m与x之间的函数关系式;(3)、试比较第8天与第10天的销售金额哪天多?22. 小王准备把牛奶加热后饮用,他先在锅中加水,再从冰箱冷藏室中拿出一杯牛奶浸入水中,用煤气灶缓慢加热.在这个过程中,他每隔测量一次水温和牛奶温度,获得数据如下表:时间
0
10
20
30
40
50
锅中水的温度
10
14
18
22
26
30
杯中牛奶的温度
6
7
8
10
12
14
 (1)、水在沸腾前,其温度是加热时间的函数,温度每秒钟升高(2)、求牛奶温度单位:与加热时间单位:之间的函数关系式.(3)、标准大气压下,水的沸点是 , 水沸腾后温度保持不变.
(1)、水在沸腾前,其温度是加热时间的函数,温度每秒钟升高(2)、求牛奶温度单位:与加热时间单位:之间的函数关系式.(3)、标准大气压下,水的沸点是 , 水沸腾后温度保持不变.①加热时间是多少时,水与牛奶的温度差最大?
②温度太高,会造成牛奶中蛋白质等营养成分损失,加热到时饮用最佳,此时,水温是多少?请通过计算说明理由.
23. 为抗击疫情,支援B市,A市某蔬菜公司紧急调运两车蔬菜运往B市.甲、乙两辆货车从A市出发前往B市,乙车行驶途中发生故障原地维修,此时甲车刚好到达B市.甲车卸载蔬菜后立即原路原速返回接应乙车,把乙车的蔬菜装上甲车后立即原路原速又运往B市.乙车维修完毕后立即返回A市.两车离A市的距离y(km)与乙车所用时间x(h)之间的函数图象如图所示.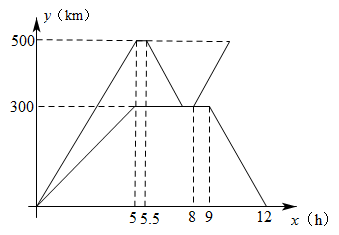 (1)、甲车速度是km/h,乙车出发时速度是km/h;(2)、求乙车返回过程中,乙车离A市的距离y(km)与乙车所用时间x(h)的函数解析式(不要求写出自变量的取值范围);(3)、乙车出发多少小时,两车之间的距离是120km?请直接写出答案.24. 为了振兴乡村经济,我市某镇鼓励广大农户种植山药,并精加工成甲、乙两种产品、某经销商购进甲、乙两种产品,甲种产品进价为8元/kg;乙种产品的进货总金额y(单位:元)与乙种产品进货量x(单位:kg)之间的关系如图所示.已知甲、乙两种产品的售价分别为12元/kg和18元/kg.
(1)、甲车速度是km/h,乙车出发时速度是km/h;(2)、求乙车返回过程中,乙车离A市的距离y(km)与乙车所用时间x(h)的函数解析式(不要求写出自变量的取值范围);(3)、乙车出发多少小时,两车之间的距离是120km?请直接写出答案.24. 为了振兴乡村经济,我市某镇鼓励广大农户种植山药,并精加工成甲、乙两种产品、某经销商购进甲、乙两种产品,甲种产品进价为8元/kg;乙种产品的进货总金额y(单位:元)与乙种产品进货量x(单位:kg)之间的关系如图所示.已知甲、乙两种产品的售价分别为12元/kg和18元/kg.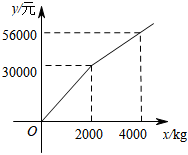 (1)、求出0≤x≤2000和x>2000时,y与x之间的函数关系式;(2)、若该经销商购进甲、乙两种产品共6000kg,并能全部售出.其中乙种产品的进货量不低于1600kg,且不高于4000kg,设销售完甲、乙两种产品所获总利润为w元(利润=销售额一成本),请求出w(单位:元)与乙种产品进货量x(单位:kg)之间的函数关系式,并为该经销商设计出获得最大利润的进货方案;(3)、为回馈广大客户,该经销商决定对两种产品进行让利销售.在(2)中获得最大利润的进货方案下,甲、乙两种产品售价分别降低a元/kg和2a元/kg,全部售出后所获总利润不低于15000元,求a的最大值.
(1)、求出0≤x≤2000和x>2000时,y与x之间的函数关系式;(2)、若该经销商购进甲、乙两种产品共6000kg,并能全部售出.其中乙种产品的进货量不低于1600kg,且不高于4000kg,设销售完甲、乙两种产品所获总利润为w元(利润=销售额一成本),请求出w(单位:元)与乙种产品进货量x(单位:kg)之间的函数关系式,并为该经销商设计出获得最大利润的进货方案;(3)、为回馈广大客户,该经销商决定对两种产品进行让利销售.在(2)中获得最大利润的进货方案下,甲、乙两种产品售价分别降低a元/kg和2a元/kg,全部售出后所获总利润不低于15000元,求a的最大值.