浙教版备考2023年中考数学一轮复习34.一次函数的动态几何问题
试卷更新日期:2022-12-25 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 如图矩形的边在轴的正半轴上,点的坐标为 , 且= . 将直线沿轴方向平移,若直线与矩形的边有公共点,则的取值范围是( )
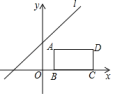 A、 B、 C、 D、2. 如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,点E,F的坐标分别为( )
A、 B、 C、 D、2. 如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,点E,F的坐标分别为( )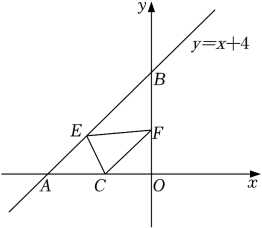 A、 , B、 , C、 , D、 ,3. 如图, 为矩形 的对角线,已知 , .点P沿折线 以每秒1个单位长度的速度运动(运动到D点停止),过点P作 于点E,则 的面积y与点P运动的路程x间的函数图象大致是( )
A、 , B、 , C、 , D、 ,3. 如图, 为矩形 的对角线,已知 , .点P沿折线 以每秒1个单位长度的速度运动(运动到D点停止),过点P作 于点E,则 的面积y与点P运动的路程x间的函数图象大致是( ) A、
A、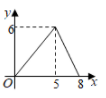 B、
B、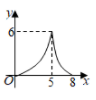 C、
C、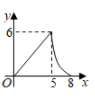 D、
D、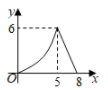 4. 如图,已知在中, , 点D沿自B向C运动,作于E,于F,则的值y与的长x之间的函数图象大致是( )
4. 如图,已知在中, , 点D沿自B向C运动,作于E,于F,则的值y与的长x之间的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 已知,直线l:与x轴交于点A,点B与点A关于y轴对称.M是直线l上的动点,将OM绕点O逆时针旋转60°得ON.连接BN,则线段BN的最小值为( )
5. 已知,直线l:与x轴交于点A,点B与点A关于y轴对称.M是直线l上的动点,将OM绕点O逆时针旋转60°得ON.连接BN,则线段BN的最小值为( )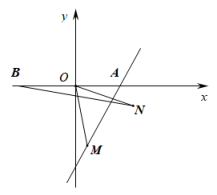 A、 B、3 C、 D、6. 如图1,在四边形 中, , ,点E沿着 的路径以2cm/s速度匀速运动,到达点 停止运动, 始终与直线 保持垂直,与 或 交于点F,设线段 的长度为 ,运动时间为 ,若d与t之间的关系如图2所示,则图中a的值为( )
A、 B、3 C、 D、6. 如图1,在四边形 中, , ,点E沿着 的路径以2cm/s速度匀速运动,到达点 停止运动, 始终与直线 保持垂直,与 或 交于点F,设线段 的长度为 ,运动时间为 ,若d与t之间的关系如图2所示,则图中a的值为( ) A、3.8 B、3.9 C、4.5 D、4.87. 如图,在平面直角坐标系中,点A1、A2、A3…An在x轴上,B1、B2、B3…Bn在直线y= 上,若A1(1,0),且△A1B1A2、△A2B2A3…△AnBnAn+1都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1、S2、S3…Sn.则Sn可表示为( )
A、3.8 B、3.9 C、4.5 D、4.87. 如图,在平面直角坐标系中,点A1、A2、A3…An在x轴上,B1、B2、B3…Bn在直线y= 上,若A1(1,0),且△A1B1A2、△A2B2A3…△AnBnAn+1都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1、S2、S3…Sn.则Sn可表示为( )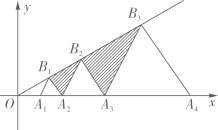 A、 B、 C、 D、8. 如图,在平面直角坐标系 xOy 中,直线 y=-x+4 与坐标轴交于 A,B 两点,OC⊥AB 于点 C,P 是线段 OC 上的一个动点,连接 AP,将线段 AP 绕点 A 逆时针旋转 45°,得到线段 AP',连接 CP',则线段 CP'的最小值为( )
A、 B、 C、 D、8. 如图,在平面直角坐标系 xOy 中,直线 y=-x+4 与坐标轴交于 A,B 两点,OC⊥AB 于点 C,P 是线段 OC 上的一个动点,连接 AP,将线段 AP 绕点 A 逆时针旋转 45°,得到线段 AP',连接 CP',则线段 CP'的最小值为( )
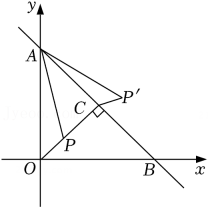 A、 B、 C、2 D、9. 如图,直线与x轴交于点B,与y轴交于点C,点 , D为线段的中点,P为y轴上的一个动点,连接、 , 当的周长最小时,点P的坐标为( )
A、 B、 C、2 D、9. 如图,直线与x轴交于点B,与y轴交于点C,点 , D为线段的中点,P为y轴上的一个动点,连接、 , 当的周长最小时,点P的坐标为( ) A、 B、 C、 D、10. 如图所示,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,0),B(5,0),C(1,4),将△ABC绕顶点A逆时针方向旋转一定角度后,点C恰好与直线y=-x-1上的点D重合,此时点B恰好与点E重合,则点E的坐标为( )
A、 B、 C、 D、10. 如图所示,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,0),B(5,0),C(1,4),将△ABC绕顶点A逆时针方向旋转一定角度后,点C恰好与直线y=-x-1上的点D重合,此时点B恰好与点E重合,则点E的坐标为( ) A、( -1, +1) B、( , +1) C、( -1, +1) D、( , +1)
A、( -1, +1) B、( , +1) C、( -1, +1) D、( , +1)二、填空题(每题4分,共18分)
-
11. 已知:直线y=-x+1与x轴、y轴分别交于点A、点B,当点P在直线上运动时,平面内存在点Q,使得以点O、P、B、Q为顶点的四边形是菱形,请你写出所有满足条件的点Q的坐标 .12. 如图1,在矩形 中,动点P从点A出发,沿 的方向在AB和BC上运动,记 ,点D到直线PA的距离为y , 且y关于x的函数图象如图2所示.当 的面积与 的面积相等时,y的值为 .
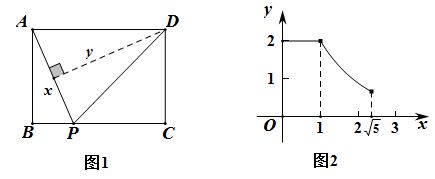 13. 如图,平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD,点C的坐标是 . 在y轴上有一个动点M,当△MDC的周长最小的时候,点M的坐标是 .
13. 如图,平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD,点C的坐标是 . 在y轴上有一个动点M,当△MDC的周长最小的时候,点M的坐标是 . 14. 如图在平面直角坐标系中,直线的图像分别与y轴和x轴交于点A,点B.定点P的坐标为 , 点Q是y轴上任意一点,则的最小值为 .
14. 如图在平面直角坐标系中,直线的图像分别与y轴和x轴交于点A,点B.定点P的坐标为 , 点Q是y轴上任意一点,则的最小值为 .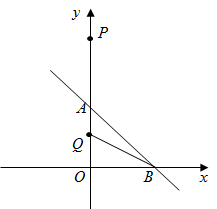 15. 如图,在长方形中,点为坐标原点,点的坐标为 , 点 , 在坐标轴上,直线与交于点 , 与轴交于点 . 动点在边上,点是坐标平面内的点.当点在第一象限,且在直线上时,若是等腰直角三角形,则点的坐标为 .
15. 如图,在长方形中,点为坐标原点,点的坐标为 , 点 , 在坐标轴上,直线与交于点 , 与轴交于点 . 动点在边上,点是坐标平面内的点.当点在第一象限,且在直线上时,若是等腰直角三角形,则点的坐标为 .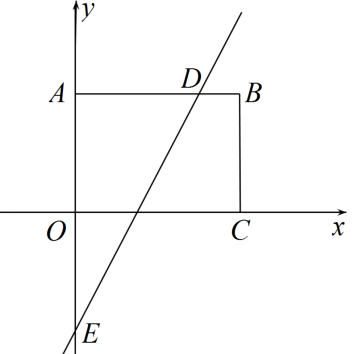 16. 在平面直角坐标系中,对于点和 , 给出如下定义:如果当时,;当时, . 那么称点Q为点P的“关联点”.例如点的“关联点”为 . 如果点是一次函数图象上点M的“关联点”,那么n的值为 .
16. 在平面直角坐标系中,对于点和 , 给出如下定义:如果当时,;当时, . 那么称点Q为点P的“关联点”.例如点的“关联点”为 . 如果点是一次函数图象上点M的“关联点”,那么n的值为 .三、解答题(共8题,共72分)
-
17. 如图所示,在平面直角坐标系中,已知点A(0,4),B(3,4),直线y= x+1上有一动点P,当PA=PB时,点P的坐标是多少?
 18. 如图,平面直角坐标系中,线段AB的端点为 , .
18. 如图,平面直角坐标系中,线段AB的端点为 , .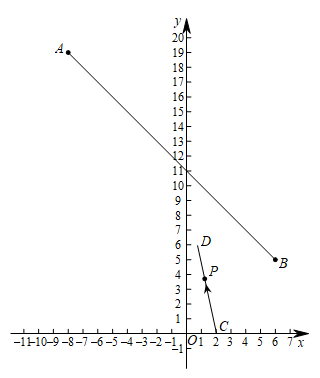 (1)、求AB所在直线的解析式;(2)、某同学设计了一个动画:在函数 中,分别输入m和n的值,使得到射线CD , 其中 .当c=2时,会从C处弹出一个光点P , 并沿CD飞行;当 时,只发出射线而无光点弹出.
(1)、求AB所在直线的解析式;(2)、某同学设计了一个动画:在函数 中,分别输入m和n的值,使得到射线CD , 其中 .当c=2时,会从C处弹出一个光点P , 并沿CD飞行;当 时,只发出射线而无光点弹出.①若有光点P弹出,试推算m , n应满足的数量关系;
②当有光点P弹出,并击中线段AB上的整点(横、纵坐标都是整数)时,线段AB就会发光,求此时整数m的个数.
19. 如图,在平面直角坐标系中,直线 分别交x轴、y轴于点B,C,正方形AOCD的顶点D在第二象限内,E是BC中点,OF⊥DE于点F,连结OE.动点P在AO上从点A向终点O匀速运动,同时,动点Q在直线BC上从某点Q1向终点Q2匀速运动,它们同时到达终点. (1)、求点B的坐标和OE的长;(2)、设点Q2为(m , n),当 tan∠EOF时,求点Q2的坐标;(3)、根据(2)的条件,当点P运动到AO中点时,点Q恰好与点C重合.①延长AD交直线BC于点Q3 , 当点Q在线段Q2Q3上时,设Q3Q=s , AP=t , 求s关于t的函数表达式.②当PQ与△OEF的一边平行时,求所有满足条件的AP的长.20. 如图,在平面直角坐标系中,一次函数 的图像与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动.点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.
(1)、求点B的坐标和OE的长;(2)、设点Q2为(m , n),当 tan∠EOF时,求点Q2的坐标;(3)、根据(2)的条件,当点P运动到AO中点时,点Q恰好与点C重合.①延长AD交直线BC于点Q3 , 当点Q在线段Q2Q3上时,设Q3Q=s , AP=t , 求s关于t的函数表达式.②当PQ与△OEF的一边平行时,求所有满足条件的AP的长.20. 如图,在平面直角坐标系中,一次函数 的图像与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动.点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.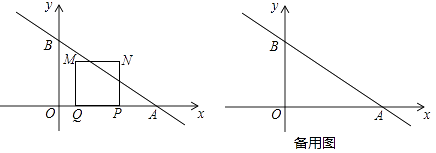 (1)、当t= 秒时,点Q的坐标是;(2)、在运动过程中,设正方形PQMN与△AOB重叠部分的面积为S,求S与t的函数表达式;(3)、若正方形PQMN对角线的交点为T,请直接写出在运动过程中OT+PT的最小值.21. 如图在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,直线与直线交于点P.
(1)、当t= 秒时,点Q的坐标是;(2)、在运动过程中,设正方形PQMN与△AOB重叠部分的面积为S,求S与t的函数表达式;(3)、若正方形PQMN对角线的交点为T,请直接写出在运动过程中OT+PT的最小值.21. 如图在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,直线与直线交于点P. (1)、A点坐标为 , P点坐标为;(2)、在线段上有一个动点M,过M点作直线轴,与直线相交于点N,若的面积为 , 求M点的坐标.(3)、若点C为线段上一动点,在平面内是否存在一点D,使得以点O,A,C,D为顶点的四边形是菱形,若存在请直接写出D点的坐标,若不存在请说明理由.22. 已知:在平面直角坐标系中,直线:与x轴,y轴分别交于A、B两点,直线经过点A,与y轴交于点 .
(1)、A点坐标为 , P点坐标为;(2)、在线段上有一个动点M,过M点作直线轴,与直线相交于点N,若的面积为 , 求M点的坐标.(3)、若点C为线段上一动点,在平面内是否存在一点D,使得以点O,A,C,D为顶点的四边形是菱形,若存在请直接写出D点的坐标,若不存在请说明理由.22. 已知:在平面直角坐标系中,直线:与x轴,y轴分别交于A、B两点,直线经过点A,与y轴交于点 .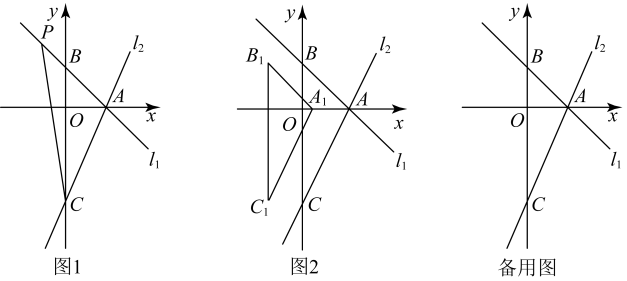 (1)、求直线的解析式;(2)、如图1,点P为直线一个动点,是否存在以点P、C、A为顶点的三角形与相似,若存在请求出点P的坐标及此时的面积.(3)、如图2,将沿着x轴平移,平移过程中的记为 , 请问在平面内是否存在点D,使得以、、C、D为顶点的四边形是菱形?若存在,直接写出点D的坐标.23. 如图1.函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)、求直线的解析式;(2)、如图1,点P为直线一个动点,是否存在以点P、C、A为顶点的三角形与相似,若存在请求出点P的坐标及此时的面积.(3)、如图2,将沿着x轴平移,平移过程中的记为 , 请问在平面内是否存在点D,使得以、、C、D为顶点的四边形是菱形?若存在,直接写出点D的坐标.23. 如图1.函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称. (1)、①直接写出点C的坐标;
(1)、①直接写出点C的坐标;②求直线BC的函数解析式;
(2)、设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q.连接BM,如图2,在点M的运动过程中是否存在点P,使∠BMP=∠BAC,若存在,请求出点P坐标;若不存在,请说明理由.24. 如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),直线l1与l2交于点C(2,m). (1)、填空:k=;b=;m=;(2)、在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由.(3)、若动点P在射线DC上从点D开始以每秒1个单位的速度运动,连接AP,设点P的运动时间为t秒.是否存在t的值,使△ACP和△ADP的面积比为1:3?若存在,直接写出t的值;若不存在,请说明理由.
(1)、填空:k=;b=;m=;(2)、在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由.(3)、若动点P在射线DC上从点D开始以每秒1个单位的速度运动,连接AP,设点P的运动时间为t秒.是否存在t的值,使△ACP和△ADP的面积比为1:3?若存在,直接写出t的值;若不存在,请说明理由.