浙教版备考2023年中考数学一轮复习33.一次函数与不等式(组)
试卷更新日期:2022-12-25 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 如图,一次函数与一次函数的图象交于点P(1,3),则关于x的不等式的解集是( )
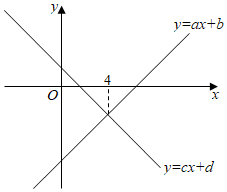
 A、 B、 C、 D、2. 在平面直角坐标系xOy中,直线:与直线:的图象如图所示,则关于x的不等式的解集为( )
A、 B、 C、 D、2. 在平面直角坐标系xOy中,直线:与直线:的图象如图所示,则关于x的不等式的解集为( )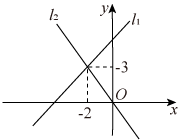 A、 B、 C、 D、3. 将直线向上平移3个单位长度后得到直线 , 下列关于直线的说法正确的是( )A、随的增大而减小 B、与轴交于点 C、经过第二、三、四象限 D、若关于的不等式 , 则4. 我们知道,若ab>0.则有或 . 如图,直线y=kx+b与y=mx+n分别交x轴于点A(-0.5,0)、B(2,0),则不等式(kx+b)(mx+n)>0的解集是( )
A、 B、 C、 D、3. 将直线向上平移3个单位长度后得到直线 , 下列关于直线的说法正确的是( )A、随的增大而减小 B、与轴交于点 C、经过第二、三、四象限 D、若关于的不等式 , 则4. 我们知道,若ab>0.则有或 . 如图,直线y=kx+b与y=mx+n分别交x轴于点A(-0.5,0)、B(2,0),则不等式(kx+b)(mx+n)>0的解集是( ) A、x>2 B、-0.5<x<2 C、0<x<2 D、x<-0.5或x>25. 如图是函数的图象.已知函数的图象与的图象交于A、B两点,且 , 则满足的x的取值范围是( )
A、x>2 B、-0.5<x<2 C、0<x<2 D、x<-0.5或x>25. 如图是函数的图象.已知函数的图象与的图象交于A、B两点,且 , 则满足的x的取值范围是( )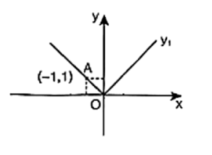 A、或 B、或 C、 D、6. 如图,直线交y轴于点A,交x轴于点B,且 , 不等式的解集为( )
A、或 B、或 C、 D、6. 如图,直线交y轴于点A,交x轴于点B,且 , 不等式的解集为( )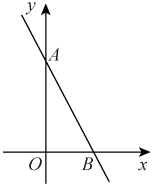 A、 B、x>3 C、 D、x<37. 如图,直线与相交于点P,点P的横坐标为 , 则关于x的不等式的解集在数轴上表示正确的是( )
A、 B、x>3 C、 D、x<37. 如图,直线与相交于点P,点P的横坐标为 , 则关于x的不等式的解集在数轴上表示正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 已知不等式的解是 , 下列有可能是函数的图像的是( )A、
8. 已知不等式的解是 , 下列有可能是函数的图像的是( )A、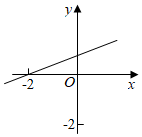 B、
B、 C、
C、 D、
D、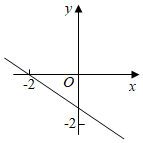 9. 如图所示,一次函数与的图象如图所示,下列说法:
9. 如图所示,一次函数与的图象如图所示,下列说法:①对于函数来说,y随x的增大而增大;②函数不经过第四象限;
③不等式的解集是;④ .

其中正确的是( )
A、2个 B、1个 C、3个 D、4个10. 数形结合是解决数学问题常用的思想方法.如图,一次函数y=kx+b(k、b为常数,且k<0)的图象与直线y=x都经过点A(3,1),当kx+b<x时,x的取值范围是( ) A、x>3 B、x<3 C、x<1 D、x>1
A、x>3 B、x<3 C、x<1 D、x>1二、填空题(每题4分,共24分)
-
11. 如图所示,一次函数与的图象如图所示,下列说法:对于函数来说,随的增大而增大;函数不经过第四象限;不等式的解集是;其中正确的是 .
 12. 如图,直线y1=2x与y2=﹣x+a交于点P(1,2),则不等式2x≥﹣x+a的解集为 .
12. 如图,直线y1=2x与y2=﹣x+a交于点P(1,2),则不等式2x≥﹣x+a的解集为 .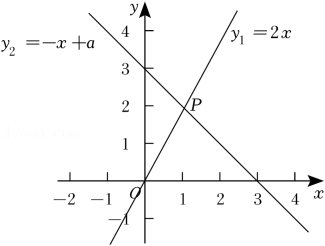 13. 如图,在平面直角坐标系中,直线:经过点 , 则关于的不等式的解集为 .
13. 如图,在平面直角坐标系中,直线:经过点 , 则关于的不等式的解集为 . 14. 如图,一次函数的图像与的图象相交于点P,则关于x的不等式的解集是 .
14. 如图,一次函数的图像与的图象相交于点P,则关于x的不等式的解集是 .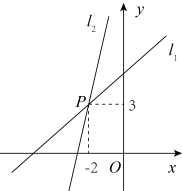 15. 若一次函数y=ax+b(a≠0)的图象经过点A(2,3),且不经过第四象限,则 4a+b的取值范围为.16. “双11”当天,重庆顺风快递公司出动所有车辆分上午、下午两批往成都送件,该公司共有甲、乙、丙三种车型,其中甲型车数量占公司车辆总数的 ,乙型车辆是丙型车数量的2倍,上午安排甲车数量的 ,乙车数量的 ,丙车数量的 进行运输,且上午甲、乙、丙三种车型每辆载货量分别为15吨,10吨,20吨,则上午刚好运完当天全部快件重量的 ;下午安排剩下的所有车辆运输完当天剩下的所有快件,且下午甲、乙、丙三种车型每辆载货量分别不得超过20吨,12吨,16吨,下午乙型车实际载货量为下午甲型车每辆实际载货量的 .已知同种货车每辆的实际载货量相等,甲、乙、丙三种车型每辆车下午的运输成本分别为50元/吨,90元/吨,60元/吨.则下午运输时,一辆甲种车、一辆乙种车、一辆丙种车总的运输成本最少为元.
15. 若一次函数y=ax+b(a≠0)的图象经过点A(2,3),且不经过第四象限,则 4a+b的取值范围为.16. “双11”当天,重庆顺风快递公司出动所有车辆分上午、下午两批往成都送件,该公司共有甲、乙、丙三种车型,其中甲型车数量占公司车辆总数的 ,乙型车辆是丙型车数量的2倍,上午安排甲车数量的 ,乙车数量的 ,丙车数量的 进行运输,且上午甲、乙、丙三种车型每辆载货量分别为15吨,10吨,20吨,则上午刚好运完当天全部快件重量的 ;下午安排剩下的所有车辆运输完当天剩下的所有快件,且下午甲、乙、丙三种车型每辆载货量分别不得超过20吨,12吨,16吨,下午乙型车实际载货量为下午甲型车每辆实际载货量的 .已知同种货车每辆的实际载货量相等,甲、乙、丙三种车型每辆车下午的运输成本分别为50元/吨,90元/吨,60元/吨.则下午运输时,一辆甲种车、一辆乙种车、一辆丙种车总的运输成本最少为元.三、解答题(共8题,共66分)
-
17. 函数图象在探索函数的性质中有非常重要的作用,现在就一类特殊的函数展开探索: ,探索函数图象和性质过程如下:
…
-6
-4
-2
-1
-0.5
0.5
1
4
6
…
…
-4
-5
5
4
5
…
(1)、上表是该函数 与自变量 的几组对应值,则 . . ; (2)、如图,在平面直角坐标系中,已经描出了表中部分点,请根据描出的点画出该函数图象;(3)、由函数图象,写出该函数的一条性质:;(4)、请在同一个平面直角坐标系中画出函数 的图象,并直接写出不等式 的解集.18. 由于灯管老化,现某学校要购进A、B两种节能灯管320只,A、B两种灯管的单价分别为25元和30元,现要求B种灯管的数量不少于A种灯管的3倍,那么购买A种灯管多少只时,可使所付金额最少?最少为多少元?19. 当自变量x满足什么条件时,的函数值不小于的函数值?20. 如图,在平面直角坐标系中,一次函数与轴交于 , 且与正比例函数图象交于点 .
(2)、如图,在平面直角坐标系中,已经描出了表中部分点,请根据描出的点画出该函数图象;(3)、由函数图象,写出该函数的一条性质:;(4)、请在同一个平面直角坐标系中画出函数 的图象,并直接写出不等式 的解集.18. 由于灯管老化,现某学校要购进A、B两种节能灯管320只,A、B两种灯管的单价分别为25元和30元,现要求B种灯管的数量不少于A种灯管的3倍,那么购买A种灯管多少只时,可使所付金额最少?最少为多少元?19. 当自变量x满足什么条件时,的函数值不小于的函数值?20. 如图,在平面直角坐标系中,一次函数与轴交于 , 且与正比例函数图象交于点 . (1)、求一次函数的解析式;(2)、直接写出时,的取值范围.21. 如图,直线与轴交于点 , 直线与轴交于点 , 两条直线交于点 .
(1)、求一次函数的解析式;(2)、直接写出时,的取值范围.21. 如图,直线与轴交于点 , 直线与轴交于点 , 两条直线交于点 . (1)、求方程组的解;(2)、当与同时成立时,求的取值范围;(3)、求的面积.22. 定义运算 min{a,b}:当 a≥b 时,min{a,b}=b;当 a<b 时,min{a,b}=a;如:min{4,0}=0;min{2,2}=2;min{﹣3,﹣1}=﹣3.根据该定义运算完成下列问题:
(1)、求方程组的解;(2)、当与同时成立时,求的取值范围;(3)、求的面积.22. 定义运算 min{a,b}:当 a≥b 时,min{a,b}=b;当 a<b 时,min{a,b}=a;如:min{4,0}=0;min{2,2}=2;min{﹣3,﹣1}=﹣3.根据该定义运算完成下列问题: (1)、min{﹣3,2}= , 当 x≤3 时,min{x,3}=;(2)、如图,已知直线 y1=x+m 与 y2=kx﹣2 相交于点 P(﹣2,1),若 min{x+m,kx﹣2}=kx﹣2,结合图象,直接写出 x 的取值范围是;(3)、若 min{3x﹣1,﹣x+3}=3﹣x,求 x 的取值范围.23. 已知:同一个坐标系中分别作出了一次函数和的图象,分别与x轴交于点A,B,两直线交于点C.已知点 , , 请你观察图象并结合一元一次方程、一元一次不等式和一次函数的相关知识回答下列问题:
(1)、min{﹣3,2}= , 当 x≤3 时,min{x,3}=;(2)、如图,已知直线 y1=x+m 与 y2=kx﹣2 相交于点 P(﹣2,1),若 min{x+m,kx﹣2}=kx﹣2,结合图象,直接写出 x 的取值范围是;(3)、若 min{3x﹣1,﹣x+3}=3﹣x,求 x 的取值范围.23. 已知:同一个坐标系中分别作出了一次函数和的图象,分别与x轴交于点A,B,两直线交于点C.已知点 , , 请你观察图象并结合一元一次方程、一元一次不等式和一次函数的相关知识回答下列问题: (1)、关于x的方程的解是;关于x的方程的解是;(2)、关于x的不等式的解集是;(3)、若点 , 请直接写出关于x的不等式的解集;(4)、请直接写出关于x的不等式组的解集.24. 请你用学习“一次函数”时积累的经验和方法研究函数的图象和性质,并解决问题.
(1)、关于x的方程的解是;关于x的方程的解是;(2)、关于x的不等式的解集是;(3)、若点 , 请直接写出关于x的不等式的解集;(4)、请直接写出关于x的不等式组的解集.24. 请你用学习“一次函数”时积累的经验和方法研究函数的图象和性质,并解决问题. (1)、按照下列步骤,画出函数的图象;
(1)、按照下列步骤,画出函数的图象;①列表;
-4
-3
-2
-1
0
1
2
3
3
2
1
0
1
2
3
4
②描点;
③连线.
(2)、观察图象,填空;①当时,随的增大而减小;时,随的增大而增大;
②此函数有最 值(填“大”或“小” ),其值是 ;
(3)、根据图象,不等式的解集为 .