浙教版备考2023年中考数学一轮复习31.一次函数与与一元一次方程

试卷更新日期：2022-12-25 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 如图，直线 $y = kx + b (k \neq 0)$ 经过点 $P (- 3.2)$ ，则关于 $x$ 的方程 $kx + b = 2$ 的解是（）

A、 $x = 1$ B、 $x = 2$ C、 $x = - 3$ D、无法确定

查看试题解析
2. 同一平面直角坐标系中，一次函数 $y = k_{1} x + b$ 的图象与 $y = k_{2} x$ 的图象如图所示，则关于x的方程 $k_{1} x + b = k_{2} x$ 的解为（）

A、 $x = 0$ B、 $x = - 1$ C、 $x = - 2$ D、以上都不对

查看试题解析
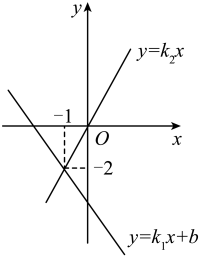3. 关于x的方程kx+b=3的解为x=7，则直线y=kx+b一定过点（）

A、(3，0) B、(7，0) C、(3，7) D、(7，3)

查看试题解析
4. 若 $x = 2$ 是关于 $x$ 的方程 $m x + n = 0 (m \neq 0 ， n > 0)$ 的解，则一次函数 $y = - m (x - 1) - n$ 的图象与 $x$ 轴的交点坐标是（）

A、 $(2 ， 0)$ B、 $(3 ， 0)$ C、 $(0 ， 2)$ D、 $(0 ， 3)$

查看试题解析

5. 若在一次函数y=ax+b(a，b是常数，a≠0)中，x与y的部分对应值如下表：

x	……	-2	-1	0	1	2	3	……
y	……	6	4	2	0	-2	-4	……

则方程ax+b=0的解是( )

A、x=2 B、x=3 C、x=-1 D、x=1

查看试题解析

6. 若方程ax+b=0的解是x=﹣2，则图中一定不是直线y=ax+b的是（　　）

A、 B、 C、 D、

查看试题解析
7. 若方程x﹣3=0的解也是直线y=（4k+1）x﹣15与x轴的交点的横坐标，则k的值为（　　）

A、-1 B、0 C、1 D、±1

查看试题解析
8. 如果一元一次方程3x﹣b=0的根x=2，那么一次函数y=3x﹣b的图象一定过点（　　）

A、（0，2） B、（2，0） C、（﹣2，0） D、（0，﹣2）

查看试题解析
9. 如图，一次函数y=kx+b图象与x轴的交点坐标是（2，0），则下列说法：①y随x的增大而减小；②b＞0；③关于x的方程kx+b=0的解为x=2．其中说法正确的是（）

A、①和② B、①和③ C、②和③ D、①②③都符合题意

查看试题解析
10. 如图，直线 $y = k x + b (k \neq 0)$ 的图象如图所示.下列结论中，正确的是（）.

A、 $k > 0$ B、方程 $k x + b = 0$ 的解为 $x = 1$ C、 $b < 0$ D、若点A（1，m）、B（3，n）在该直线图象上，则m＜n

查看试题解析

二、填空题（每题4分，共24分）

11. 当一次函数y=kx+b的函数值为时，相应的自变量值即为一元一次方程kx+b=0的解；
一次函数y=kx+b的图象与轴的交点的横坐标即为一元一次方程kx+b=0的解．

查看试题解析
12. 如图，直线AB是一次函数 $y = k x + k - 1$ 的图象，若关于x的方程 $k x + k - 1 = 0$ 的解是 $x = - \frac{2}{3}$ ，则直线AB的函数关系式为．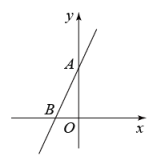

查看试题解析
13. 已知直线y=x+b和y=ax+2交于点P（3，-1），则关于x的方程（a-1）x=b-2的解为．

查看试题解析
14. 已知关于x的方程mx+n=0的解是x=-2，则直线y=mx+n与x轴的交点坐标是．

查看试题解析
15. 已知一次函数 $y = k x - b$ （k、b为常数，且 $k \neq 0$ ， $b \neq 0$ ）与 $y = \frac{1}{3} x$ 的图象相交于点 $M (a ， \frac{1}{2})$ ，则关于x的方程 $(k - \frac{1}{3}) x = b$ 的解为 $x =$ ．

查看试题解析
16. 直线l： $y = k x + b$ （k、b是常数， $k \neq 0$ ）经过 $A (0 ， 2)$ 、 $B (- 1 ， m)$ 两点，其中 $m < 0$ ，下列四个结论：①方程 $k x + b = 0$ 的解在 $- 1$ 和0之间；②若点 $P_{1} (x_{1} ， y_{1})$ 、 $P_{2} (x_{1} + 1 ， y_{2})$ 在直线l上，则 $y_{1} > y_{2}$ ；③ $k > 2$ ；④不等式 $k x + b > - m$ 的解集为 $x > - \frac{1}{3}$ 时， $k = 3$ ，其中正确的结论有.（只需填写序号）

查看试题解析

三、解答题（共6题，共66分）

17. 已知一次函数 $y = k x + b (k \neq 0)$ 的图象经过点 $(3 ， 5)$ 与 $(- 4 ， - 9)$ .

(1)、求这个一次函数的解析式；

(2)、判断点 $C (\frac{1}{2} ， 0)$ 是否在这个一次函数的图象上；

(3)、直接写出关于x的一元一次方程kx＋b＝0的解.

查看试题解析
18. 画出函数y＝2x+6的图象，利用图象：

(1)、求方程2x+6＝0的解；

(2)、求不等式2x+6＞0的解；

(3)、若﹣2≤y≤2，求x的取值范围．

查看试题解析
19. 如图，根据一次函数y=kx+b的图象，直接写出下列问题的答案：

(1)、关于x的方程kx+b=0的解；

(2)、当x=1时，代数式k+b的值；

(3)、关于x的方程kx+b=-3的解。

查看试题解析
20. 在初中阶段的函数学习中，我们知道由含有未知数 $x$ 和 $y$ 的两个二元一次方程组成的每个二元一次方程组，都对应两个一次函数；同时知道任何一个以 $x$ 为未知数的一元一次不等式都可以变形为 $a x + b \geq 0$ 或 $a x + b \leq 0 (a \neq 0)$ 的形式，因此我们可以用画一次函数图象的方法得到方程组的解或不等式的解集.

(1)、在给出的平面直角坐标系中，直接画出函数 $y = - x + 2$ 的图象；

(2)、如图，直线 $y = k x + b (k > 0 ， b > 0)$ 与 $y = - x + 2$ 相交于点 $(- 1 ， m)$ ，根据图象直接写出关于 $x$ 的方程 $k x + b = - x + 2$ 的解；

(3)、根据图象直接写出不等式 $k x + b \leq - x + 2$ 的解集.

查看试题解析

21. 阅读与理解：

小亮在学习完八年级下册后，结合前面所学知识对“求一元一次方程的解”整理得出以下几种方法，请仔细阅读并完成相应的任务：

数学复习笔记
专题：一元一次方程解法	时间：2021年6月×日
引例：求一元一次方程 $2 x + 1 = 4 - x$ 的解
方法一：按照七年级解一元一次方程的步骤求解．	移项，合并同类项，未知数系数化1 ……
方法二：将方程移项，合并同类项得 $3 x - 3 = 0$ ，如图，把此方程的解看成一个一次函数的图象与 $x$ 轴交点的横坐标，由图可知该方程的解为 $x = 1$ ．
方法三：方程 $2 x + 1 = 4 - x$ 的解可以看成两个一次函数 $y = 2 x + 1$ 和 $y = 4 - x$ 的交点的横坐标，由图可知该方程的解为 $x = 1$ ．

任务：

(1)、方法二和方法三共同体现的一个数学思想是；（只填序号）

①数形结合思想；②公理化思想；③分类讨论思想；④整体思想

(2)、依据“方法二”的思路，直接写出图一中对应的一次函数表达式为；

(3)、参照“方法三”的思路，求解一元一次方程

\frac{1}{2} x + 1 = x - 1

的解时，请在图的平面直角坐标系中画出相应的函数图象并依据图象直接写出方程的解．

查看试题解析

22. 请根据学习“一次函数”时积累的经验和方研究函数 $y = - | x | + 2$ 的图象和性质，并解决问题.

(1)、填空：
①当x＝0时， $y = - | x | + 2 =$ ；

②当x＞0时， $y = - | x | + 2 =$ ；

③当x＜0时， $y = - | x | + 2 =$ ；

(2)、在平面直角坐标系中作出函数 $y = - | x | + 2$ 的图象；

(3)、观察函数图象，写出关于这个函数的两条结论；

(4)、进一步探究函数图象发现：
①函数图象与x轴有个交点，方程 $- | x | + 2 = 0$ 有个解；

②方程 $- | x | + 2 = 2$ 有个解；

③若关于x的方程 $- | x | + 2 = a$ 无解，则a的取值范围是.

查看试题解析