浙教版备考2023年中考数学一轮复习29.函数及其表示法
试卷更新日期:2022-12-24 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 已知整式① ,② ,若 ,则下列说法正确的是( )A、①与②的和是常数 B、①与②的差是常数 C、①与②的积是常数 D、①与②的和、差、积都与t的值有关2. 正方形的周长y是边长x的函数,则下列表示正方形周长y与边长x之间的函数关系正确的是( )A、 B、 C、 D、3. 暑假期间,同学们打出租车去重庆欢乐谷游玩,出租车在公路上行驶了一段后,就遇上了堵车,停止不前,后来为了赶时间,出租车加快速度前往重庆欢乐谷.设同学们从上出租车开始所用的时间为自变量x,离欢乐谷的距离为因变量y.下列图象中能正确表示同学们从上出租车到抵达重庆欢乐谷整个过程中变量y与x关系的是( )A、
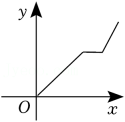 B、
B、 C、
C、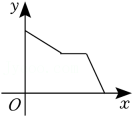 D、
D、 4. 下列图象中,表示y是x的函数的是( )A、
4. 下列图象中,表示y是x的函数的是( )A、 B、
B、 C、
C、 D、
D、 5. 路程 ,速度 ,时间 三者之间的关系式为 ,当其中一个量是常量时,另外两个变量的函数图象不可能是( )A、
5. 路程 ,速度 ,时间 三者之间的关系式为 ,当其中一个量是常量时,另外两个变量的函数图象不可能是( )A、 B、
B、 C、
C、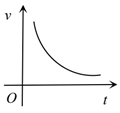 D、
D、 6. 在某次实验中,测得两个变量m和v之间的4组对应数据如下表:
6. 在某次实验中,测得两个变量m和v之间的4组对应数据如下表:m
1
2
3
4
v
2.01
4.9
10.03
17.1
则m与v之间的关系最接近于下列各关系式中的( )
A、v=2m B、v=m2+1 C、v=3m-1 D、v=m+17. 小明想用实验的方法测量某种食用油的沸点,他找到一个秒表和一支刻度标有0—100℃的温度计.他在锅中加入一定量的这种食用油,在煤气灶上加热,并且每隔10秒测一次温度,他发现加热到第100秒时,油沸腾了.以下是他的测量数据:时间t/s
0
10
20
30
40
油温y/℃
10
30
50
70
90
下面说法不正确的是( )
A、加热到30秒时油温是70℃ B、估计这种食用油的沸点温度是210℃ C、在这个问题中,时间和油温都是变量,其中油温是自变量 D、在一定范围内,每加热10秒,油温上升20℃8. 下列所描述的四个变化过程中,变量之间的关系不能看成函数关系的是( )A、三角形的一个外角度数度和与它相邻的内角度数度的关系 B、树的高度为60厘米,每个月长高3厘米,月后树的高度为厘米,与的关系 C、正方形的面积(平方厘米)和它的边长(厘米)的关系 D、一个正数的平方根是 , 随着这个数的变化而变化,与之间的关系9. 如图,矩形ABCD中,AB=2,BC=4,P为矩形边上的一个动点,运动路线是A→B→C→D→A,设点P经过的路程为x,以A,P,B为顶点的三角形面积为y,则下列图象能大致反映y与x的函数关系的是( ) A、
A、 B、
B、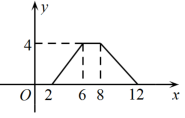 C、
C、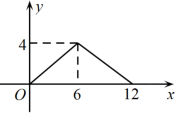 D、
D、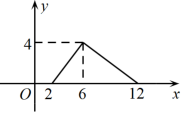 10. 已知y1和y2均是以x为自变量的函数,当x=n时,函数值分别是N1和N2 , 若存在实数n,使得N1+N2=1,则称函数y1和y2是“和谐函数”.则下列函数y1和y2不是“和谐函数”的是( )A、y1=x2+2x和y2=﹣x+1 B、y1=和y2=x+1 C、y1=﹣和y2=﹣x﹣1 D、y1=x2+2x和y2=﹣x﹣1
10. 已知y1和y2均是以x为自变量的函数,当x=n时,函数值分别是N1和N2 , 若存在实数n,使得N1+N2=1,则称函数y1和y2是“和谐函数”.则下列函数y1和y2不是“和谐函数”的是( )A、y1=x2+2x和y2=﹣x+1 B、y1=和y2=x+1 C、y1=﹣和y2=﹣x﹣1 D、y1=x2+2x和y2=﹣x﹣1二、填空题(每空4分,共32分)
-
11. 函数y=的定义域为 .12. 当时,函数的值是 .13. 长方形的周长为10cm , 其中一边为xcm(其中x>0),另一边为ycm , 则y关于x的函数表达式为 .14. 从甲地向乙地打长途电话,按时间收费,3分钟内收费2.4元,每加1分钟加收1元,若时间t≥3(分)时,电话费y(元)与t(分)之间的函数关系式是 .15. 定义: ,例如: , ,当 时,函数 的最小值为 .16. 甲乙两位同学住在同一小区,学校与小区相距2700米,一天甲从小区步行出发去学校,12分钟后乙先骑共享自行车,途经学校又骑行一段路到达还车点后,立即步行走回学校.已知步行速度甲比乙每分钟快5米.图中的折线表示甲乙两人之间的距离y(米)与甲步行时间x(分钟)的函数关系图像,根据图像可知:甲步行速度为米/分;乙骑自行车的速度为米/分;乙到还车点时,甲乙两人相距米.

三、综合题(共7题,共58分)
-
17. 根据下表写出y与x之间的一个关系式,并求出表中m , n的值
x
﹣2
﹣1
0
1
2
3
4
y
n
6
0
﹣6
﹣12
﹣18
m
18. 父亲告诉张云:“距离地面越高,温度越低”,并给张云出示了下面的表格:距离地面高度(千米)
0
1
2
3
4
5
温度(℃)
20
14
8
2
-4
-10
根据上表,父亲还给张云出了下面几个问题,请你和张云一起回答.
(1)、上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、如果用h表示距离地面的高度,用t表示温度,那么随着的变化,是怎么变化的?(3)、你能猜出距离地面6千米的高空温度是多少吗?19. 司机小王开车从地出发去地送信,其行驶路与行驶时间之间的关系如图所示,当汽车行驶若干小时到达地时,汽车发生了故障,需停车检修,修理了几小时后,为了按时赶到地,汽车加快了速度,结果正好按时赶到,根据题意结合图回答下列问题: (1)、上述问题中反映的是哪两个变量之间的关系?指出自变量和因变量.(2)、汽车从地到地用了几小时?平均每小时行驶多少千米?(3)、汽车停车检修了多长时间?车修好后每小时走多少千米?20. 小亮和爸爸登山,两人距离地面的高度y(米)与小亮登山时间x(分)之间的函数图象分别如图中折线和线段所示,根据函数图象进行以下探究:
(1)、上述问题中反映的是哪两个变量之间的关系?指出自变量和因变量.(2)、汽车从地到地用了几小时?平均每小时行驶多少千米?(3)、汽车停车检修了多长时间?车修好后每小时走多少千米?20. 小亮和爸爸登山,两人距离地面的高度y(米)与小亮登山时间x(分)之间的函数图象分别如图中折线和线段所示,根据函数图象进行以下探究: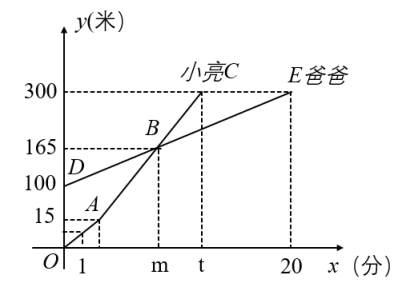 (1)、爸爸开始登山时距离地面米,登山的速度是每分钟米.(2)、求爸爸登山时距地面的高度y(米)与登山时间x(分)之间的函数关系式.(3)、小亮和爸爸什么时候相遇?求出相遇的时间.(4)、若小亮提速后,他登山的速度是爸爸速度的3倍,问小亮登山多长时间时开始提速?21. 某中学七年级开展了“双减”下劳动实践活动,组织学生到实践基地割麦.张敏与同学从学校出发到实践基地,割完麦后,按原路返回.途中到小卖部买水,然后返回学校,张敏与同学离学校的距离y(米)与所用时间x(分钟)之间的关系如图所示.学校、小卖部、实践基地在同一直线上.
(1)、爸爸开始登山时距离地面米,登山的速度是每分钟米.(2)、求爸爸登山时距地面的高度y(米)与登山时间x(分)之间的函数关系式.(3)、小亮和爸爸什么时候相遇?求出相遇的时间.(4)、若小亮提速后,他登山的速度是爸爸速度的3倍,问小亮登山多长时间时开始提速?21. 某中学七年级开展了“双减”下劳动实践活动,组织学生到实践基地割麦.张敏与同学从学校出发到实践基地,割完麦后,按原路返回.途中到小卖部买水,然后返回学校,张敏与同学离学校的距离y(米)与所用时间x(分钟)之间的关系如图所示.学校、小卖部、实践基地在同一直线上. (1)、学校到实践基地的距离为 m,小卖部到实践基地的距离为 m;(2)、张敏与同学在实践基地停留了多长时间?他们在小卖部买水用了多长时间?(3)、若他们上午8:00从学校出发,那么他们几点回到学校?22. 学习一次函数时,我们通过列表、描点、连线画出一次函数图象,并结合函数图象研究函数性质。小南结合学习一次函数的经验,对函数的图像和性质进行了研究,下面是小南的探讨过程,请补充完整:(1)、列表:
(1)、学校到实践基地的距离为 m,小卖部到实践基地的距离为 m;(2)、张敏与同学在实践基地停留了多长时间?他们在小卖部买水用了多长时间?(3)、若他们上午8:00从学校出发,那么他们几点回到学校?22. 学习一次函数时,我们通过列表、描点、连线画出一次函数图象,并结合函数图象研究函数性质。小南结合学习一次函数的经验,对函数的图像和性质进行了研究,下面是小南的探讨过程,请补充完整:(1)、列表:x
…
-2
-1
0
1
2
3
…
y
…
m
1
2
3
2
n
…
表格中 , ;
(2)、
①根据列表在给出的平面直角坐标系中描点、画出函数图象;
②根据所画的函数图象,该函数有(填“最大值”或“最小值”);这个值为;
(3)、直接写出函数图象与x轴所围成的图形的面积:;(4)、过点作直线l//x轴,结合所画的函数图象,若直线l与函数图像有两个交点,请直接写出a的取值范围.23. 通过一次函数的学习,我们积累了学习函数性质的经验和方法,请你利用所学知识来探究函数的性质,解决以下问题:(1)、填表,并画出该函数的图象.①列表:
x
……
0
1
2
3
4
……
y
……
3
2
0
1
2
4
5
……
②描点;

③连线.
(2)、研究函数性质:观察图象,发现函数的其中一条性质为;(3)、观察画出的图象,当函数的值大于3时,直接写出x的取值范围.