浙教版备考2023年中考数学一轮复习28.坐标与图形的性质

试卷更新日期：2022-12-24 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 如图，在平面直角坐标系 $x O y$ 中，线段 $A B$ 两端点的坐标分别为 $A (3 ， 0)$ ， $B (2 ， 2)$ ，以点 $P (1 ， 0)$ 为位似中心，将线段 $A B$ 放大得线段 $C D$ ，若点 $C$ 坐标为 $(7 ， 0)$ ，则点 $D$ 的坐标为（）

A、 $(3 ， 6)$ B、 $(4 ， 6)$ C、 $(5 ， 6)$ D、 $(6 ， 6)$

查看试题解析
2. 如图，菱形OABC在平面直角坐标系中的位置如图所示， $∠ A O C = 45 °$ ， $O A = 2$ ，则点C的坐标为（）

A、 $(\sqrt{2} ， 1)$ B、 $(\sqrt{2} ， \sqrt{2})$ C、 $(1 ， \sqrt{2})$ D、 $(\sqrt{2} + 1 ， 1)$

查看试题解析
3. 如图，平面直角坐标系中，已知A（2，2）、B（4，0）.若在坐标轴上取点C，使△ABC为等腰三角形，则满足条件的点C的个数是（）

A、5 B、6 C、7 D、4

查看试题解析
4. 如图，在平面直角坐标系中，将边长为2的正六边形 $O A B C D E$ 绕点 $O$ 顺时针旋转 $n$ 个 $45 °$ ，得到正六边形 $O A_{n} B_{n} C_{n} D_{n} E_{n}$ ，当 $n = 2022$ 时，正六边形 $O A_{n} B_{n} C_{n} D_{n} E_{n}$ 的顶点 $D_{n}$ 的坐标是（）

A、 $(- \sqrt{3} ， - 3)$ B、 $(- 3 ， - \sqrt{3})$ C、 $(3 ， - \sqrt{3})$ D、 $(- \sqrt{3} ， 3)$

查看试题解析
5. 如图，在平面直角坐标系中，点M为x轴正半轴上一点，过点M的直线l∥y轴，且直线l分别与反比例函数 $y = \frac{8}{x}$ 和 $y = \frac{k}{x}$ 的图象交于P、Q两点.若S_△POQ＝15，则k的值为（）

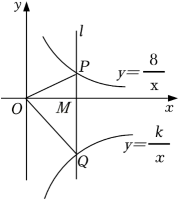A、38 B、22 C、﹣7 D、﹣22

查看试题解析
6. 如图，直线AB交x轴于点C，交反比例函数y＝ $\frac{a - 1}{x}$ （a＞1）的图象于A、B两点，过点B作BD⊥y轴，垂足为点D，若S_△BCD＝5，则a的值为（）

A、8 B、9 C、10 D、11

查看试题解析
7. 如图，在平面直角坐标系中，0为坐标原点，A点坐标(6，0)，B点坐标(3，-3)，动点P从A点出发，沿x轴正方向运动，连接BP，以BP为直角边向下作等腰直角三角形BPC，∠PBC=90°，连结OC，当OC=10时，△OCP的面积为（）

A、16 $\sqrt{2}$ B、64 C、32 D、36

查看试题解析
8. 如图，已知点A，B的坐标分别为 $(1 ， 1)$ ， $(- 2 ， - 1)$ ，四边形 $A C D B$ 是平行四边形，点C的坐标为 $(4 ， 1)$ ，则点D的坐标为（）

A、 $(1 ， - 1)$ B、 $(2 ， 1)$ C、 $(2 ， - 1)$ D、 $(- 2 ， 3)$

查看试题解析
9. 如图，点A坐标为 $(0 ， - 2)$ ，直线 $y = - \frac{1}{2} x + 3$ 分别交x轴，y轴于点N，M，点B是线段MN上一点，连结AB.现以AB为边，点A为直角顶点构造等腰直角 $△ A B C$ .若点C恰好落在x轴上，则点B的坐标为（　　）

A、 $(1 ， \frac{3}{2})$ B、 $(2 ， 2)$ C、 $(3 ， \frac{9}{2})$ D、 $(4 ， 5)$

查看试题解析
10. 将等腰△ABC如图1放置，使得底边BC与x轴重合，此时点A的坐标为 $(2 ， \sqrt{5})$ ，若将该三角形如图2放置，使得腰长AB与x轴重合，则此时C点的坐标为（）

A、 $(\frac{8}{3} ， \frac{10}{3})$ B、 $(\frac{5}{2} ， \frac{4 \sqrt{5}}{3})$ C、 $(\frac{5}{2} ， \frac{4 \sqrt{3}}{3})$ D、 $(\frac{8}{3} ， \frac{4 \sqrt{5}}{3})$

查看试题解析

二、填空题（每题3分，共18分）

11. 如图，把矩形OABC放在平面直角坐标系中，OC在x轴上，OA在y轴上，且OC=4，OA=8，把矩形OABC绕着原点顺时针旋转90°得到矩形ODEF，则点E的坐标为

查看试题解析
12. 如图，在平面直角坐标系中， $△ O A B$ 为等腰三角形， $O A = A B = 5$ ，点B到x轴的距离为4，若将 $△ O A B$ 绕点O逆时针旋转 $90 °$ ，得到 $△ O A^{'} B^{'}$ ，则点 $B^{'}$ 的坐标为.

查看试题解析
13. 三个能够重合的正六边形的位置如图.已知B点的坐标是（﹣ $\sqrt{3}$ ，3），则A点的坐标是

查看试题解析
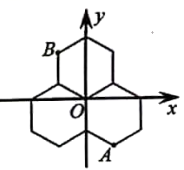14. 已知以点C（a，b）为圆心，半径为r的圆的标准方程为（x﹣a）²+（y﹣b）²＝r² ．例如：以A（2，3）为圆心，半径为2的圆的标准方程为（x﹣2）²+（y﹣3）²＝4，则以原点为圆心，过点P（1，1）的圆的标准方程为.

查看试题解析
15. 在平面直角坐标系中，我们把横、纵坐标都是整数的点叫做整点.如图，若“心形”图形的顶点A，B，C，D，E，F，G均为整点，已知点P（3，4），线段PQ的长为 $\sqrt{10}$ ， PQ关于过点M（0，5）的直线l对称得到P'Q'，点P的对应点为P′，当点P′恰好落在“心形”图形边的整点上时，点Q'也落在“心形”图形边的整点上，则这样的点Q′共有个.

查看试题解析
16. 如图，点 $A$ ， $B$ 在反比例函数 $y = \frac{k}{x} (x > 0 ， k > 0)$ 的图象上（点 $A$ 在点 $B$ 的右侧），过点 $A$ ， $B$ 分别作 $x$ 轴和 $y$ 轴的平行线相交于点 $C$ ，图中 $△ A B C$ ， $△ B C O$ ， $△ A C O$ 的面积分别记为 $S_{1}$ ， $S_{2}$ ， $S_{3}$ .若 $S_{1} = 2 S_{3}$ ， $S_{2} = 5$ ，则 $k$ 的值为.

查看试题解析

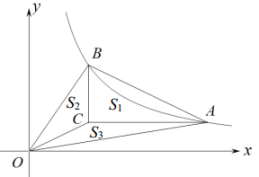
三、解答题（共8题，共72分）

17. “水城河畔，樱花绽放，凉都宫中，书画成风”的风景，引来市民和游客争相“打卡”留念．已知水城河与南环路之间的某路段平行宽度为200米，为避免交通拥堵，请在水城河与南环路之间设计一条停车带，使得每个停车位到水城河与到凉都宫点 $F$ 的距离相等．

(1)、利用尺规作出凉都宫到水城河的距离（保留作图痕迹，不写作法）；

(2)、在图中格点处标出三个符合条件的停车位 $P_{1}$ ， $P_{2}$ ， $P_{3}$ ；

(3)、建立平面直角坐标系，设 $M (0 ， 2)$ ， $N (2 ， 0)$ ，停车位 $P (x ， y)$ ，请写出 $y$ 与 $x$ 之间关系式，在图中画出停车带，并判断点 $P (4 ， - 4)$ 是否在停车带上．

查看试题解析
18. 如图，在平面直角坐标系中， $R t △ A B C$ 的顶点 $A$ ， $B$ 在坐标轴上， $∠ B A C = 90 °$ ， $O A = O B = 4$ ， $A B = 2 A C$ ，求 $A C$ 所在直线的解析式.

查看试题解析
19. 如图，直线 $y = k_{1} x + b$ 与反比例函数 $y = \frac{k_{2}}{x}$ 的图象交于A $(1 ， 6)$ ，B $(a ， 3)$ 两点.

(1)、求 $k_{1}$ 、 $k_{2}$ 的值？

(2)、直接写出 $k_{1} x + b - \frac{k_{2}}{x} > 0$ 时x的取值范围？

(3)、如图，等腰梯形OBCD中，BC//OD，OB=CD，OD边在x轴上，过点C作CE⊥OD于点E，CE和反比例函数的图象交于点P，当梯形OBCD的面积为12时，请判断PC和PE的大小关系，并说明理由.

查看试题解析
20. 如图，二次函数 $y_{1} = x^{2} + m x + 1$ 的图象与y轴相交于点A，与反比例函数 $y_{2} = \frac{k}{x} (x > 0)$ 的图象相交于点B(3，1).

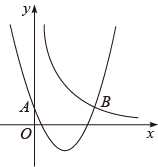(1)、求这两个函数的表达式；

(2)、当 $y_{1}$ 随x的增大而增大且 $y_{1} < y_{2}$ 时，直接写出x的取值范围；

(3)、平行于x轴的直线l与函数 $y_{1}$ 的图象相交于点C、D（点C在点D的左边），与函数 $y_{2}$ 的图象相交于点E.若△ACE与△BDE的面积相等，求点E的坐标.

查看试题解析
21. 如图，平面直角坐标系中，四边形OABC为矩形，点A，B的坐标分别为（3，0），（3，4）．动点M从点O出发，以每秒1个单位的速度沿线段OA向终点A运动，同时点N以相同速度从点B出发，沿线段BC向终点C运动，过点N作NP⊥BC，交AC于点P，连接MP，设运动时间为t秒．

(1)、求直线AC的解析式．

(2)、用含t的代数式表示P的坐标（直接写出答案）．

(3)、是否存在t的值，使以P，A，M为顶点的三角形与△AOC相似？若存在，请求出t的值；若不存在，请说明理由．

查看试题解析
22. 定义：在平面直角坐标系中，M（x₁ ， y₁），N（x₂ ， y₂），x₁≠x₂ ， y₁≠y₂ ，且点M，N在同一象限，过点M，N分别作x轴的垂线，垂足分别为点G，F，若 $| y_{1} | > | y_{2} |$ ，则过点M作y轴的垂线，交直线NF于点E，如图1.我们称矩形MEFG为过点M，N的伴随矩形.
已知：如图2，点A（1，3），点B是反比例函数 $y = \frac{k}{x} （ x > 0 ）$ 图象上的两点.

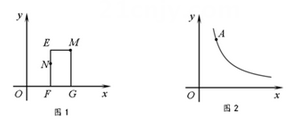(1)、求k的值.

(2)、若过点A，B的伴随矩形是正方形，求点B的坐标.

(3)、若过点A，B的伴随矩形的面积是3，求点B的坐标.

查看试题解析
23. 在平面直角坐标系xOy中，点B的坐标为（0，4 $\sqrt{3}$ ），以OB为边在y轴的右侧作正三角形OAB.AC⊥y轴，垂足为C.

(1)、如图1，求点A的坐标.

(2)、点D在线段AC上，点E是直线AB上一动点，连接DE、以DE为边作正三角形DEF（点D，E，F按逆时针排列）
①如图2，当点E与点A重合时，连接OD，BF.若BF=2 $\sqrt{7}$ ，求点D的坐标.
②若CD=2，点P是直线DF与直线OA的交点，当OP= $\sqrt{3}$ 时，直接写出点E的坐标.

查看试题解析
24. 【发现问题】
小明在练习簿的横线上取点 $O$ 为圆心，相邻横线的间距为半径画圆，然后半径依次增加一个间距画同心圆，描出了同心圆与横线的一些交点，如图1所示，他发现这些点的位置有一定的规律．
【提出问题】
小明通过观察，提出猜想：按此步骤继续画圆描点，所描的点都在某二次函数图象上．

(1)、【分析问题】
小明利用已学知识和经验，以圆心 $O$ 为原点，过点 $O$ 的横线所在直线为 $x$ 轴，过点 $O$ 且垂直于横线的直线为 $y$ 轴，相邻横线的间距为一个单位长度，建立平面直角坐标系，如图2所示．当所描的点在半径为5的同心圆上时，其坐标为．

(2)、【解决问题】
请帮助小明验证他的猜想是否成立．

(3)、【深度思考】
小明继续思考：设点 $P (0 ， m)$ ， $m$ 为正整数，以 $O P$ 为直径画 $⊙ M$ ，是否存在所描的点在 $⊙ M$ 上．若存在，求 $m$ 的值；若不存在，说明理由．

查看试题解析