浙教版备考2023年中考数学一轮复习26.一元一次不等式组的解法及应用
试卷更新日期:2022-12-24 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 下列不等式组是一元一次不等式组的是( )A、 B、 C、 D、2. 不等式组的解集表示在数轴上正确的是( )A、
 B、
B、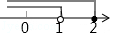 C、
C、 D、
D、 3. 已知不等式 , 其解集在数轴上表示正确的是( )A、
3. 已知不等式 , 其解集在数轴上表示正确的是( )A、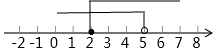 B、
B、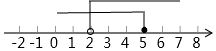 C、
C、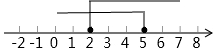 D、
D、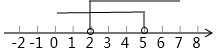 4. 若关于的分式方程的解为非负数,且关于的不等式组有3个整数解,则所有满足条件的整数的值之和为( )A、19 B、22 C、30 D、335. 下列是在数轴上表示不等式组的解集,其中表示此不等式组无解的是( )A、
4. 若关于的分式方程的解为非负数,且关于的不等式组有3个整数解,则所有满足条件的整数的值之和为( )A、19 B、22 C、30 D、335. 下列是在数轴上表示不等式组的解集,其中表示此不等式组无解的是( )A、 B、
B、 C、
C、 D、
D、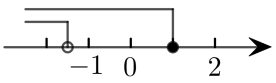 6. 已知关于的不等式组的所有整数解的和为-5,则的取值范围为( )A、或 B、或 C、 D、7. 关于x的不等式组只有两个整数解,且 , 要使的值是整数,则符合条件的a个数是( )A、3 B、4 C、5 D、68. 某商店甲商品的单价为8元,乙商品的单价为2元.已知购买乙商品的件数比购买甲商品的件数的2倍少4件,如果购买甲、乙两种商品的总件数不少于32,且购买甲、乙两种商品的总费用不超过148元.设购买甲商品x件,依题意可列不等式组得( )A、 B、 C、 D、9. 运行程序如图所示,规定:从“输入一个值x”到“结果是否95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是( )
6. 已知关于的不等式组的所有整数解的和为-5,则的取值范围为( )A、或 B、或 C、 D、7. 关于x的不等式组只有两个整数解,且 , 要使的值是整数,则符合条件的a个数是( )A、3 B、4 C、5 D、68. 某商店甲商品的单价为8元,乙商品的单价为2元.已知购买乙商品的件数比购买甲商品的件数的2倍少4件,如果购买甲、乙两种商品的总件数不少于32,且购买甲、乙两种商品的总费用不超过148元.设购买甲商品x件,依题意可列不等式组得( )A、 B、 C、 D、9. 运行程序如图所示,规定:从“输入一个值x”到“结果是否95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是( ) A、 B、 C、 D、10. 把一些图书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人至少有一本,但不到3本.那么这些图书有( ).A、26本 B、25本 C、24本 D、23本
A、 B、 C、 D、10. 把一些图书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人至少有一本,但不到3本.那么这些图书有( ).A、26本 B、25本 C、24本 D、23本二、填空题(每题4分,共24分)
-
11. 运行程序如图所示,规定:从“输入一个值x”到“结果是否>5”为一次程序操作,如果程序操作进行了两次才停止,那么x的取值范围是 .
 12. 把一筐苹果分给几个学生,如果每人分3个,那么余8个;如果每人分5个,那么最后一人分到,但不足3个.设学生有x人,列不等式组为 .13. 不等式组的解集是 .14. 已知关于的不等式组的解集为 , 则.15. 在平面直角坐标系中,若点在第二象限,则整数m的值为 .16. 若关于x的不等式组的整数解为1,2,3,求适合条件的有序整数对的个数 .
12. 把一筐苹果分给几个学生,如果每人分3个,那么余8个;如果每人分5个,那么最后一人分到,但不足3个.设学生有x人,列不等式组为 .13. 不等式组的解集是 .14. 已知关于的不等式组的解集为 , 则.15. 在平面直角坐标系中,若点在第二象限,则整数m的值为 .16. 若关于x的不等式组的整数解为1,2,3,求适合条件的有序整数对的个数 .三、解答题(共8题,共66分)
-
17. 以下是圆圆解不等式组的解答过程:
解:由①,得 , 所以 .
由②,得 , 所以 ,
所以 . 所以原不等式组的解是 .
圆圆的解答过程是否有错误?如果有错误,请写出正确的解答过程.
18. 化简: , 并从不等式组的解集中选择一个合适的整数解代入求值.19. 已知:关于的方程组的解为负数,求的取值范围.20. 解不等式组并写出该不等式组的最小整数解.21. 解不等式组 , 在数轴上表示该不等式组的解集,且求出满足该不等式组的所有整数解的和. 22. 定义:给定两个不等式组和 , 若不等式组的任意一个解,都是不等式组的一个解,则称不等式组为不等式组的“子集”.
22. 定义:给定两个不等式组和 , 若不等式组的任意一个解,都是不等式组的一个解,则称不等式组为不等式组的“子集”.例如:不等式组:是:的“子集”.
(1)、若不等式组:: , : , 则其中不等式组是不等式组:的“子集”填A或B);(2)、若关于的不等式组是不等式组的“子集”,则的取值范围是;(3)、已知 , , , 为不互相等的整数,其中 , , 下列三个不等式组:: , : , :满足:是的“子集”且是的“子集”,求的值.23. 若不等式组只有个正整数解为自然数 , 则称这个不等式组为阶不等式组 .我们规定:当时,这个不等式组为阶不等式组 .
例如:不等式只有4个正整数解,因此称其为4阶不等式.
不等式组只有3个正整数解,因此称其为3阶不等式组.
请根据定义完成下列问题:
(1)、 是阶不等式;是阶不等式组;(2)、若关于的不等式组是4阶不等式组,求的取值范围;(3)、关于的不等式组的正整数解有 , , , , 其中如果是阶不等式组,且关于的方程的解是的正整数解 , 请求出的值以及的取值范围.
24. 某公司在甲、乙工厂代工同一产品,表1是两个工厂产品的收费标准,表2是两个工厂的代工记录(a,b为常数,m,n都为不大于10的正整数),代工费用由加工费和制版费两部分组成,制版费与件数无关.已知甲、乙两工厂第一次代工合计500件,且两工厂收费相同.表1
收费内容工厂
单件加工费
制版费
甲
10元
2000元
乙
25元
0
表2
时间
甲工厂代工记录
乙工厂代工记录
第一次
a件
b件
第二次
(a+100m)件
(b+100n)件
(1)、求a,b的值.(2)、若m+n=12,第二次分配到甲工厂的代工件数小于分配到乙工厂的代工件数的2倍,求甲、乙两工厂第二次代工总费用的最小值.(3)、若甲工厂代工效率为20件每小时,乙工厂代工效率为40件每小时,第二次甲、乙两工厂代工总费用估计在42000到44000元之间(包括42000,44000),求出所有满足条件的代工分配方案,并指出哪种方案代工总时长最短.