江西省部分名校2022-2023学年高一上学期数学12月大联考试卷

试卷更新日期：2022-12-23 类型：月考试卷

进入出卷网下载

一、单选题

1. 命题“ $\exists x < 3$ ， $2^{x} - x < 3$ ”的否定是（）

A、 $\exists x < 3$ ， $2^{x} - x \geq 3$ B、 $\forall x < 3$ ， $2^{x} - x > 3$ C、 $\forall x \geq 3$ ， $2^{x} - x \geq 3$ D、 $\forall x < 3$ ， $2^{x} - x \geq 3$

查看试题解析
2. 若全集 $U = {- 3 ， - 2 ， 1 ， 2 ， 4 ， 5} ， A = {1 ， 2 ， 5} ， B = {- 2 ， 1 ， 2}$ ，则集合 ${- 3 ， 4} =$ （）

A、 $∁_{U} (A \cap B)$ B、 $∁_{U} (A ∪ B)$ C、 $(∁_{U} A) \cap B$ D、 $A \cup (∁_{U} B)$

查看试题解析
3. 函数 $f (x) = - x^{3} - x + 20$ 的零点所在的区间是（）

A、 $(0 ， 1)$ B、 $(1 ， 2)$ C、 $(2 ， 3)$ D、 $(3 ， 4)$

查看试题解析
4. $2022$ 年 $11$ 月 $1$ 日凌晨 $4$ 点 $27$ 分，梦天实验舱与天和核心舱成功实现“太空握手”.对接时，只有空间站组合体与梦天实验舱处于同一轨道高度，且空间站组合体前向对接口朝向了梦天舱赶上来的方向，才能实现“太空握手”.根据以上信息，可知“梦天实验舱与天和核心舱成功实现‘太空握手’”是“空间站组合体与梦天实验舱处于同一轨道高度”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
5. 已知函数 $f (x) = x^{2} - 2 a x + 7$ 在 $[7 ， + \infty)$ 上单调递增，则 $a$ 的取值范围为（）

A、 $[7 ， + \infty)$ B、 $[\frac{7}{2} ， + \infty)$ C、 $(- \infty ， 7]$ D、 $(- \infty ， \frac{7}{2}]$

查看试题解析
6. 函数 $f (x) = (x^{2} - 2) l n (| x | + 2)$ 的大致图象是（）

A、 B、 C、 D、

查看试题解析
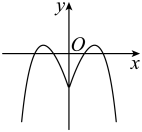7. 已知某种药在病人血液中的量不低于900mg才有疗效，现给某病人静脉注射了3000mg该种药若该种药在血液中以每小时19%的比例衰减，经过n小时失去疗效，则n（）（参考数据lg3≈0.477）

A、5 B、6 C、7 D、8

查看试题解析
8. 已知 $f (x)$ 是定义域为 $R$ 的奇函数，当 $x \geq 0$ 时， $f (x) = 2^{x} + x^{2} - 1$ ，若对于任意 $x \in [0 ， + \infty)$ ，不等式 $f (x^{2} + t) \geq 2 f (x) - x^{2} + 2 x + 2$ 恒成立，则 $t$ 的最小值是（）

A、1 B、 $\frac{5}{4}$ C、 $- \frac{3}{2}$ D、 $- 2$

查看试题解析

二、多选题

9. 已知函数 $f (x)$ 的图象如图所示，若幂函数 $g (x)$ 和函数 $f (x)$ 的图象恰有2个公共点，则 $g (x)$ 的解析式可能是（）

A、 $g (x) = \frac{1}{x}$ B、 $g (x) = \frac{1}{2} x$ C、 $g (x) = x^{2}$ D、 $g (x) = x^{3}$

查看试题解析
10. 已知f（x）为奇函数，函数 $g (x) = f (x) - \frac{1}{x} + 1 ，$ 若 $f (1) = 4 ， g (- 2) = \frac{1}{2} ，$ 则（）

A、 $g (- 1) = - 2$ B、 $f (- 2) = 2$ C、 $f (2) = 1$ D、 $g (2) = \frac{5}{2}$

查看试题解析
11. 若 $a = 8^{0.34} ， b = {(\frac{1}{36})}^{0.05} ， c = l o g_{5} \frac{31}{2} ， d = l o g_{3} \frac{24}{5}$ 则（）

A、a>c B、c>d C、b>d D、a>b

查看试题解析
12. 已知函数 $f (x) = {\begin{array}{l} - x^{2} + 2 x ， 0 \leq x \leq 2 \\ \frac{1}{2} f (x - 2) ， x > 2 \end{array}$ ，则（）

A、 $f (x)$ 的值域为 $[0 ， + \infty)$ B、 $f (x)$ 在 $[2 k ， 2 k + 1] (k \in N^{*})$ 上单调递增 C、对任意 $x \in [\frac{7}{2} ， + ∞) ， f (x) \leq \frac{3}{8}$ 恒成立 D、函数 $g (x) = f (x) - \frac{1}{4} | {(\frac{1}{2})}^{x} - 1 |$ 有6个零点

查看试题解析

三、填空题

13. 若函数 $f (x) = a^{x} - 9 (a > 0$ 且 $a \neq 1)$ 的图象过定点 $P$ ，则 $P$ 的坐标为.

查看试题解析
14. 若函数 $f (x)$ 和 $g (x)$ 的值域相同，但定义域不同，则称 $f (x)$ 和 $g (x)$ 是“同象函数”.已知函数 $f (x) = x^{2} + 2$ ，写出一个与 $f (x)$ 是“同象函数”的函数 $g (x)$ 的解析式： $g (x) =$ .

查看试题解析
15. 已知 $x > 0$ ，则 $4^{x + 1} + \frac{1}{4^{x} - 1}$ 的最小值为.

查看试题解析
16. 已知 $f (x)$ 是定义域为R的函数，且 $\forall x \in R$ ， $f (x + 1) \cdot f (x - 4) = - 1$ ，且 $f (- 3) = \frac{1}{5}$ ，则 $f (2022)$ = ，

查看试题解析

四、解答题

17.

(1)、若 $3 a + 2 b = 2$ ，求 $\frac{{(5^{a})}^{4} \cdot 2 5^{b}}{5^{a}}$ 的值；

(2)、求值： $l o g_{6} 3 \cdot l o g_{3} 7 \cdot l o g_{7} 9 + l o g_{6} (l o g_{2} 16)$ .

查看试题解析
18. 已知集合 $A = {x ∣ x^{2} - 3 x - 18 \leq 0} ， B = {x ∣ m - 5 \leq x \leq 2 m}$ .

(1)、若 $m = 1$ ，求 $A \cap B$ ；

(2)、若 $A \cup B = A$ ，求 $m$ 的取值范围.

查看试题解析
19. 某公司有两种活期理财产品，投资周期最多为一年，产品一：投资1万元，每月固定盈利40元.产品二：投资1万元，前 $x (1 \leq x \leq 12 ， x \in N_{+})$ 个月的总盈利 $f (x)$ （单位：元）与 $x$ 的关系式为 $f (x) = a x^{2} + b x$ ，已知小明选择了产品二，第一个月盈利10元，前两个月盈利30元.

(1)、求 $f (x)$ 的解析式；

(2)、若小红有1万元，根据小红投资周期的不同，探讨她在产品一和产品二中选择哪一个能获得最大盈利.

查看试题解析
20. 如函数 $f (x) = l o g_{3} (x + 12) + l o g_{3} (6 - x)$ .

(1)、求 $f (x)$ 的定义域.

(2)、从下面①②两个问题中任意选择一个解答，如果两个都解答，按第一个解答计分.
①求不等式 $f (x) - l o g_{3} 5 < 2$ 的解集.
②求 $f (x)$ 的最大值.

查看试题解析
21. 已知函数 $f (x) = 3 - \frac{1}{3^{x} + 1}$ .

(1)、求 $f (x)$ 的值域；

(2)、若正数 $a ， b$ 满足 $f (a - 2) + f (b - 3) = 5$ ，求 $\frac{1}{a + 1} + \frac{4}{b + 3}$ 的最小值.

查看试题解析
22. 已知函数 $f (x) = l o g_{a} (a^{2 x} + 1) + k x (a > 0$ ，且 $a \neq 1)$ 是偶函数.

(1)、求 $k$ 的值；

(2)、若 $a = 2$ ，函数 $g (x) = [f (x) + m] [f (x) - 4 m] + 6 m^{2}$ ，讨论 $g (x)$ 零点的个数.

查看试题解析