湖湘名校教育联合体五市十校教研教改共同体2023届高三第二次大联考数学试题

试卷更新日期：2022-12-23 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知 $A = {y | y = a^{x} (a ⟩ 0 ， a \neq 1)}$ ， $B = {x | x^{2} > x}$ ，则 $A ∩ B =$ （）

A、 $(0 ， + ∞)$ B、 $(1 ， + \infty)$ C、 $(- ∞ ， 0)$ D、 $(- \infty ， 0) \cup (1 ， + \infty)$

查看试题解析
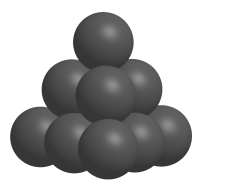
2. 在平面直角坐标系中，角 $α$ 的顶点与原点重合，始边与 $x$ 轴非负半轴重合，则“ $α = \frac{π}{3}$ ”是“角 $α$ 的终边过点 $(1 ， \sqrt{3})$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 已知函数 $f (x) = e^{- x} - e^{x} + \frac{1}{x} + 3$ ，若 $f (m) = 2$ ，则 $f (- m) =$ （）

A、 $- 2$ B、 $- 4$ C、 $2$ D、 $4$

查看试题解析
4. 高阶等差数列是数列逐项差数之差或高次差相等的数列，中国古代许多著名的数学家对推导高阶等差数列的求和公式很感兴趣，创造并发展了名为“垛积术”的算法，展现了聪明才智 $.$ 如南宋数学家杨辉在《详解九章算法 $.$ 商功》一书中记载的三角垛、方垛、刍甍垛等的求和都与高阶等差数列有关 $.$ 如图是一个三角垛，最顶层有 $1$ 个小球，第二层有 $3$ 个，第三层有 $6$ 个，第四层有 $10$ 个，则第 $30$ 层小球的个数为（）

A、 $464$ B、 $465$ C、 $466$ D、 $495$

查看试题解析
5. 已知实数 $a ， b ， c$ 满足 $2 \times 3^{a} - 3^{b + 1} = 0$ ， $\sqrt[3]{b} + 1 = \sqrt[3]{c}$ ， $a = c + l o g_{5} (x^{2} - x + 3) (x \in R)$ ，则 $a ， b ， c$ 的大小关系是（）

A、 $a > b > c$ B、 $b > c > a$ C、 $c > b > a$ D、 $a > c > b$

查看试题解析
6. 已知 $c o s (\frac{π}{2} + α) = \sqrt{2} s i n (α - \frac{π}{4})$ ，则 $\frac{s i n 2 α + 2}{c o s 2 α + 1} =$ （）

A、 $\frac{5}{4}$ B、 $\frac{7}{4}$ C、 $7$ D、 $- 7$

查看试题解析
7. 在平面直角坐标系中，已知点 $M (2 ， 0)$ ， $N (- 1 ， 0)$ ，动点 $Q (x ， y)$ 满足 $| Q M | = 2 | Q N |$ ，过点 $(- 3 ， 1)$ 的直线与动点 $Q$ 的轨迹交于 $A$ ， $B$ 两点，记点 $Q$ 的轨迹的对称中心为 $C$ ，则当 $△ A B C$ 面积取最大值时，直线 $A B$ 的方程是（）

A、 $y = x + 4$ B、 $y = - x + 4$ C、 $y = 2 x + 4$ D、 $y = - 2 x + 4$

查看试题解析
8. 已知菱形 $A B C D$ 的边长为 $2$ ， $∠ B A D = 6 0^{∘}$ ，将 $△ B C D$ 沿对角线 $B D$ 翻折，使点 $C$ 到点 $P$ 处，且二面角 $A - B D - P$ 的平面角的余弦值为 $- \frac{1}{3}$ ，则此时三棱锥 $P - A B D$ 的外接球的体积与该三棱锥的体积比值为（）

A、 $\frac{2 \sqrt{2}}{3}$ B、 $\frac{8 \sqrt{2} π}{3}$ C、 $4 π$ D、 $6 \sqrt{2} π$

查看试题解析

二、多选题

9. 已知 $a$ ， $b$ ， $c$ ， $d \in R$ ，则下列命题正确的有（）

A、若 $a < b$ ，则 $a^{3} < b^{3}$ B、若 $a < b < 0$ ，则 $a^{2} < a b < b^{2}$ C、若 $a > b$ ， $c > d$ ，则 $l n (a + c) > l n (b + d)$ D、若 $0 < \frac{1}{a} < \frac{1}{b}$ ，则 $\frac{b}{a} < \frac{b + 1}{a + 1}$

查看试题解析
10. 如图，正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为 $1$ ， $P$ 为线段 $A_{1} D$ 上的一个动点，下列结论中正确的是（）

A、 $B P ⊥ B C$ B、 $B P / /$ 平面 $C B_{1} D_{1}$ C、 $P$ 到 $A$ 和到 $B_{1}$ 的距离之和的最小值为 $\sqrt{2 + \sqrt{2}}$ D、 $P B$ 与 $C D$ 所成角的正切值的最小值为 $\frac{\sqrt{2}}{2}$

查看试题解析
11. 已知 $F$ 是抛物线 $C ： x^{2} = 2 y$ 的焦点， $A ， B$ 是抛物线 $C$ 上的两点， $O$ 为坐标原点，则（）

A、若 $A F ⊥ y$ 轴，则 $| A F | = 1$ B、若 $| A F | = 2$ ，则 $△ A O F$ 的面积为 $\frac{\sqrt{3}}{4}$ C、 $A B$ 长度的最小值为 $2$ D、若 $∠ A O B = 9 0^{∘}$ ，则 $| O A | \cdot | O B | \geq 8$

查看试题解析
12. 已知函数 $f (x) = e^{x} - x$ ， $g (x) = x - l n x$ ，则下列说法正确的是（）

A、 $g (e^{x})$ 在 $(0 ， + ∞)$ 上是增函数 B、 $\forall x > 1$ ，不等式 $f (a x) \geq f (l n x^{2})$ 恒成立，则正实数 $a$ 的最小值为 $\frac{2}{e}$ C、若 $f (x) = t$ 有两个零点 $x_{1} ， x_{2}$ ，则 $x_{1} + x_{2} > 0$ D、若 $f (x_{1}) = g (x_{2}) = t (t > 2)$ ，且 $x_{2} > x_{1} > 0$ ，则 $\frac{l n t}{x_{2} - x_{1}}$ 的最大值为 $\frac{1}{e}$

查看试题解析

三、填空题

13. 已知复数 $z$ 满足 $z \cdot (1 + i) = | 1 + i |$ ，则 $z =$ ．

查看试题解析
14. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边为 $a$ ， $b$ ， $c$ ，且 $a = 2$ ， $b = 3$ ， $c = 4$ ，则 $\vec{A B} \cdot \vec{B C} + \vec{B C} \cdot \vec{C A} + \vec{C A} \cdot \vec{A B}$ 的值等于．

查看试题解析
15. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的离心率 $e \geq 2$ ，直线 $y = - x + 1$ 交双曲线于点 $M$ ， $N$ ， $O$ 为坐标原点且 $O M ⊥ O N$ ，则双曲线实轴长的最小值是．

查看试题解析
16. 已知函数 $f (x) = 1 + x - \frac{x^{2}}{2} + \frac{x^{3}}{3} - \frac{x^{4}}{4} + ⋯ + \frac{x^{2023}}{2023}$ ， $g (x) = 1 - x + \frac{x^{2}}{2} - \frac{x^{3}}{3} + \frac{x^{4}}{4} - ⋯ - \frac{x^{2023}}{2023}$ ，设 $F (x) = f (x + 5) \cdot g (x - 3)$ ，且函数 $F (x)$ 的零点均在区间 $[a ， b] (a < b$ ， $a$ ， $b \in Z)$ 内，则 $b - a$ 的最小值为．

查看试题解析

四、解答题

17. 已知函数 $f (x) = 2 s i n x c o s x + 2 \sqrt{3} c o s^{2} x - \sqrt{3}$ ．

(1)、求函数 $f (x)$ 的最小正周期和单调递减区间；

(2)、当 $x \in [0 ， \frac{π}{2}]$ 时，求函数 $f (x)$ 的值域．

查看试题解析
18. 已知二项式 ${(\sqrt{2} x^{2} - \sqrt{\frac{1}{2} x})}^{2 n}$ 的展开式的各项系数和构成数列 ${a_{n}} .$ 数列 ${b_{n}}$ 的首项 $b_{1} = 1$ ，前 $n$ 项和为 $S_{n} (S_{n} \neq 0)$ ，且当 $n \geq 2$ 时，有 $2 S_{n}^{2} = 2 b_{n} S_{n} - b_{n} (n \geq 2)$ ．

(1)、求 $a_{n}$ 和 $S_{n}$ ；

(2)、设数列 ${\frac{(- 1)^{n} a_{n}}{S_{n}}}$ 的前 $n$ 项和为 $T_{n}$ ，若 $λ (T_{2 n} + \frac{1}{9}) \leq \frac{1}{9}$ 对任意的正整数 $n$ 恒成立，求实数 $λ$ 的取值范围．

查看试题解析
19. 如图，在四棱椎 $P - A B C D$ 中，底面 $A B C D$ 为平行四边形， $P A ⊥$ 平面 $A B C D$ ，点 $M$ ， $N$ 分别为 $B C$ ， $P A$ 的中点．

(1)、取 $P B$ 的中点 $H$ ，连接 $A H$ ，若平面 $A H C ⊥$ 平面 $P A B$ ，求证： $P B ⊥ A C$ ；

(2)、已知 $A B = A C = 1$ ， $A D = \sqrt{2}$ ，若直线 $A C$ 与平面 $P B C$ 所成角的正弦值为 $\frac{\sqrt{3}}{3}$ ，求平面 $P B C$ 与平面 $A B C D$ 的夹角的余弦值．

查看试题解析
20. 如图，在直角三角形 $A B C$ 中， $A = \frac{π}{2}$ ， $A B = 3 ， A C = 4 ， D 、 E 、 F$ 分别在线段 $A C 、 A B 、 B C$ 上，且 $D$ 为 $A C$ 的中点， $D E ⊥ D F$ ，设 $∠ A D E = α$ ．

(1)、求 $s i n ∠ D F C$ (用 $α$ 表示)；

(2)、求三角形 $D E F$ 面积的最小值．

查看试题解析
21. 如图，在平面直角坐标系 $x O y$ 中，已知椭圆 $\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ 的左、右顶点分别为 $A ， B$ ，过左焦点 $F_{1}$ 的直线与椭圆交于点 $P ， Q$ （点 $Q$ 在点 $P$ 的上方）．

(1)、求证：直线 $A P ， A Q$ 的斜率乘积为定值；

(2)、过点 $P ， Q$ 分别作椭圆的切线，设两切线交于点 $M$ ，证明： $M F_{1} ⊥ P Q$ ．

查看试题解析
22. 已知函数 $f (x) = 2 l n x - a x^{2} + b x (a ， b \in R)$ ．

(1)、当 $b = 0$ 时，讨论 $f (x)$ 的单调性 $；$

(2)、设 $x_{1} ， x_{2}$ 为 $f (x)$ 的两个不同零点，证明：当 $x \in (0 ， + \infty)$ 时， $f (x_{1} + x_{2}) < 4 s i n (x_{1} + x_{2}) + 2 e^{x_{1} + x_{2} - 2}$ ．

查看试题解析