湖南省长沙市四校2022-2023学年高二上学期数学期中联考试卷（B卷）

试卷更新日期：2022-12-23 类型：期中考试

进入出卷网下载

一、单选题

1. 若数列 $- 9$ ， $m$ ， $x$ ， $n$ ， $- 16$ 是等比数列，则 $x$ 的值是（）

A、12 B、 $\pm 12$ C、 $- 12$ D、 $- 12.5$

查看试题解析
2. 已知方程 $\frac{x^{2}}{3 + k} + \frac{y^{2}}{2 - k} = 1$ 表示椭圆，则 $k$ 的取值范围为（）

A、 $k > - 3$ 且 $k \neq - \frac{1}{2}$ B、 $- 3 < k < 2$ 且 $k \neq - \frac{1}{2}$ C、 $k > 2$ D、 $k < - 3$

查看试题解析
3. 等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，若 $S_{30} = 90$ ， $S_{90} = 30$ ，则 $S_{120} =$ （）

A、 $- 30$ B、 $- 120$ C、 $- 180$ D、 $- 240$

查看试题解析
4. 已知数列 ${a_{n}}$ ， ${b_{n}}$ 满足 $a_{n} = e^{b_{n}}$ ， $n \in N^{*}$ ，其中 ${b_{n}}$ 是等差数列，且 $a_{5} \cdot a_{2018} = e^{- 2}$ ，则 $b_{1} + b_{2} + ⋯ + b_{2022} =$ （）

A、2022 B、－2022 C、 $l n 2022$ D、1011

查看试题解析
5. 椭圆 $\frac{x^{2}}{9} + \frac{y^{2}}{2} = 1$ 的左、右焦点分别为 $F_{1}$ 、 $F_{2}$ ，动点A在椭圆上，B为椭圆的上顶点，则 $△ A B F_{2}$ 周长的最大值为（）

A、8 B、10 C、12 D、16

查看试题解析
6. 已知圆 $C ： {(x + 1)}^{2} + y^{2} = 10$ ，直线 $l ： x + 3 y + m = 0$ ，若 $l$ 上存在点 $P$ ，过 $P$ 作圆 $C$ 的两条切线，切点分别为 $A ， B$ ，使得 $∠ A P B = 60^{\circ}$ ，则 $m$ 的取值范围为（）

A、 $[- \sqrt{10} ， 2 \sqrt{10}]$ B、 $[- 10 ， 19]$ C、 $[- 21 ， 19]$ D、 $[- 19 ， 21]$

查看试题解析
7. 已知 $E F$ 是棱长为8的正方体外接球的一条直径，点M在正方体表面上运动，则 $\vec{M E} \cdot \vec{M F}$ 的最小值为（）

A、 $- 48$ B、 $- 32$ C、 $- 16$ D、0

查看试题解析
8. 设 $S_{n}$ 是数列 ${a_{n}}$ 的前 $n$ 项和， $S_{n} = \frac{3}{2} a_{n} - 3^{n + 1}$ ，若不等式 $a_{n} \geq \frac{2 n^{2} + n}{\sqrt{k}}$ 对任意 $n \in N_{+}$ 恒成立，则 $k$ 的最小值为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{6}$ C、 $\frac{1}{9}$ D、 $\frac{1}{36}$

查看试题解析

二、多选题

9. 若 ${a_{n}}$ 是等差数列，则下列数列中仍为等差数列的是（）

A、 ${| a_{n} |}$ B、 ${a_{n + 1} - a_{n}}$ C、 ${p a_{n} + q}$ ( $p ， q$ 为常数) D、 ${2 a_{n} + n}$

查看试题解析
10. 已知椭圆 $C ： \frac{x^{2}}{25} + \frac{y^{2}}{9} = 1 ， F_{1} ， F_{2}$ 分别为它的左､右焦点， $A ， B$ 为椭圆的左､右顶点，点 $P$ 是椭圆上异于 $A ， B$ 的一个动点，则下列结论中正确的有（）

A、 $△ F_{1} P F_{2}$ 的周长为15 B、若 $∠ F_{1} P F_{2} = 9 0^{∘}$ ，则 $△ F_{1} P F_{2}$ 的面积为9 C、 $\vec{P F_{1}} \cdot \vec{P F_{2}} - \vec{P A} \cdot \vec{P B}$ 为定值 D、直线 $P A$ 与直线 $P B$ 斜率的乘积为定值

查看试题解析
11. 已知直线 $l ： x \sin α - y \cos α - 1 = 0$ 与圆 $O ： x^{2} + y^{2} = 6$ 相交于 $A$ ， $B$ 两点，则（）

A、 $△ A O B$ 的面积为定值 B、 $\cos ∠ A O B = - \frac{2}{3}$ C、圆 $O$ 上总存在3个点到直线 $l$ 的距离为2 D、线段 $A B$ 中点的轨迹方程是 $x^{2} + y^{2} = 1$

查看试题解析
12. 古希腊毕达哥拉斯学派的数学家用沙粒和小石子来研究数，他们根据沙粒或小石子所排列的形状，把数分成许多类，如图中第一行图形中黑色小点个数：1，3，6，10，…称为三角形数，第二行图形中黑色小点个数：1，4，9，16，…称为正方形数，记三角形数构成数列 ${a_{n}}$ ，正方形数构成数列 ${b_{n}}$ ，则下列说法正确的是（）

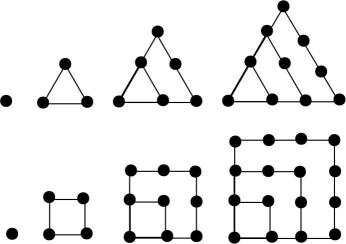A、 $\frac{1}{a_{1}} + \frac{1}{a_{2}} + \frac{1}{a_{3}} + ⋯ + \frac{1}{a_{n}} = \frac{n}{n + 1}$ B、1225既是三角形数，又是正方形数 C、 $\frac{1}{b_{1}} + \frac{1}{b_{2}} + \frac{1}{b_{3}} + ⋯ + \frac{1}{b_{n}} < \frac{33}{20}$ D、 $\forall m \in N^{*} ， m \geq 2$ ，总存在 $p ， q \in N^{*}$ ，使得 $b_{m} = a_{p} + a_{q}$ 成立

查看试题解析

三、填空题

13. 设等差数列{an}的前n项之和为Sn满足S₁₀﹣S₅＝20，那么a₈＝.

查看试题解析
14. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ， $a_{1} = 1$ ， $S_{n} - (2 n - 1) S_{n - 1} = n^{2} a_{n} (n \geq 2 ， n \in N^{*})$ ，则数列 $S_{n} =$ ．

查看试题解析
15. 已知圆 $C ： x^{2} + y^{2} - 2 a x + 4 y = 0$ 关于直线 $x + 3 y + 2 = 0$ 对称， $P (x ， y)$ 为圆C上一点，则 $2 x - y$ 的最大值为．

查看试题解析
16. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右焦点 $F (c ， 0) (b > c)$ 和上顶点B，若斜率为 $\frac{6}{5}$ 的直线l交椭圆C于P，Q两点，且满足 $\vec{F B} + \vec{F P} + \vec{F Q} = \vec{0}$ ，则椭圆的离心率为.

查看试题解析

四、解答题

17. 已知直线 $l ： k x - y + 2 k + 1 = 0 (k \in R) .$

(1)、求证：直线l过定点，并求出此定点；

(2)、求点 $A (3 ， 0)$ 到直线l的距离的最大值.

查看试题解析
18. 设等差数列{an}的前n项和为Sn，a₈=4，a₁₃=14.

(1)、求数列{an}的通项公式；

(2)、求Sn的最小值及相应的n的值；

(3)、在公比为q的等比数列{bn}中，b₂=a₈ ， b₁+b₂+b₃=a₁₃ ，求 $q + q^{4} + q^{7} + \dots + q^{3 n + 4}$ .

查看试题解析
19. 已知正项数列 ${a_{n}}$ 满足 $a_{1} = 2$ 且 $a_{n + 1}^{2} - 6 a_{n}^{2} + a_{n} a_{n + 1} = 0$ ．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、令 $b_{n} = {\begin{array}{l} l o g_{2} a_{n}^{2} ， n 为奇数 \\ a_{n} ， n 为偶数 \end{array}$ ，求数列 ${b_{n}}$ 的前 $2 n + 1$ 项的和 $S_{2 n + 1}$ ．

查看试题解析
20. 如图，在四棱锥 $P - A B C D$ 中，四边形 $A B C D$ 是矩形， $A D ⊥$ 平面 $P A B ， P A ⊥ P B$ ， E为 $A D$ 的中点．
.

(1)、若点M在线段 $P B$ 上，试确定点M的位置使得直线 $E M / /$ 平面 $P C D$ ．并证明；

(2)、若 $A P = A D ， A B = \sqrt{2} A D$ ，求平面 $P C E$ 与平面 $P A B$ 所成角的余弦值．

查看试题解析
21. 记数列{an}的前n项和为Sn，bn＝an_＋₁－Sn，且{bn}是以－1为公差的等差数列，a₁＝2，a₂＝3．

(1)、求{an}的通项公式；

(2)、求数列{an ${b_{n}}^{2}$ }的前n项和．

查看试题解析
22. 如图，椭圆 $Q ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右焦点为 $F (c ， 0)$ ，过点F的一动直线m绕点F转动，并且交椭圆于A､B两点，P为线段 $A B$ 的中点.

(1)、求点P的轨迹H的方程；

(2)、在Q的方程中，令 $a^{2} = 1 + c o s θ + s i n θ ， b^{2} = s i n θ (0 < θ \leq \frac{π}{2})$ ，确定 $θ$ 的值，使原点距椭圆的右准线l最远，此时，设l与x轴交点为D，当直线m绕点F转动到什么位置时，三角形 $A B D$ 的面积最大？

查看试题解析