山东省济宁市泗水县2022-2023学年高三上学期数学期中考试试卷

试卷更新日期：2022-12-22 类型：期中考试

进入出卷网下载

一、单选题

1. 设集合 $A = {x \in Z | - 1 \leq x \leq 2}$ ， $B = {x | x^{2} < 2}$ ，则 $A \cap B =$ （）

A、 ${- 1 ， 0 ， 1}$ B、 ${0}$ C、 ${- 1 ， 0}$ D、 ${- 1 ， 0 ， 1 ， 2}$

查看试题解析
2. 定义运算 $| \begin{matrix} a & b \\ c & d \end{matrix} | = a d - b c$ ，若复数 $z$ 满足 $| \begin{matrix} z i & - 1 \\ z & 1 \end{matrix} | = 1 - i$ ，则 $\bar{z} =$ （）

A、 $1 + i$ B、 $1 - i$ C、 $- i$ D、 $i$

查看试题解析
3. 设 $a$ ， $b \in R$ ，则“ $l n \frac{a}{b} > 0$ ”是“ $l n a > l n b$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 已知命题 $p ： \exists m \in R$ ， $f (x) = 3^{x} - m \log_{2} x$ 是增函数，则 $\neg p$ 为（）

A、 $\exists m \in R$ ， $f (x) = 3^{x} - m \log_{2} x$ 是减函数 B、 $\forall m \in R$ ， $f (x) = 3^{x} - m \log_{2} x$ 是增函数 C、 $\exists m \in R$ ， $f (x) = 3^{x} - m \log_{2} x$ 不是增函数 D、 $\forall m \in R$ ， $f (x) = 3^{x} - m \log_{2} x$ 不是增函数

查看试题解析
5. 设 $a = \log_{5} 2$ ， $b = \log_{9} 3$ ， $c = \log_{15} 4$ ，则（）

A、 $c < b < a$ B、 $b < c < a$ C、 $a < c < b$ D、 $a < b < c$

查看试题解析
6. 如图，圆 $O$ 的直径 $A B = 4$ ，点C，D是半圆弧 $A B$ 上的两个三等分点，则 $\vec{A C} \cdot \vec{A D} =$ （）

A、4 B、 $4 \sqrt{3}$ C、 $2 \sqrt{3}$ D、6

查看试题解析
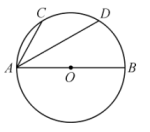7. 我国古代数学名著《孙子算经》载有一道数学问题：“今有物不知其数，三三数之剩二，五五数值剩二，七七数之剩二，问物几何？”根据这一数学思想，所以被3除余2的自然数从小到大组成数列 ${a_{n}}$ ，所有被5除余2的自然数从小到大组成数列 ${b_{n}}$ ，把 ${a_{n}}$ 和 ${b_{n}}$ 的公共项从小到大得到数列 ${c_{n}}$ ，则（）

A、 $a_{3} + b_{5} = c_{3}$ B、 $b_{28} = c_{10}$ C、 $a_{5} b_{2} > c_{8}$ D、 $c_{9} - b_{9} = a_{26}$

查看试题解析
8. 定义在 $R$ 上的偶函数 $f (x)$ 在 $[0, 1]$ 上单调递减，且满足 $f (x + 1) = - f (x)$ ， $f (π) = 1$ ， $f (2 π) = 2$ ，则不等式组 ${\begin{cases} 1 \leq x \leq 2, \\ 1 \leq f (x) \leq 2 \end{cases}$ 的解集为（）

A、 $[1, \frac{π}{2}]$ B、 $[2 π - 6, 4 - π]$ C、 $[π - 2, \frac{π}{2}]$ D、 $[π - 2, 8 - 2 π]$

查看试题解析

二、多选题

9. 下列结论正确的是（）

A、若 $\vec{A B} \cdot \vec{A C} < 0$ ，则 $△ A B C$ 是钝角三角形 B、若 $a \in R$ ，则 $a + \frac{3}{a} \geq 2 \sqrt{3}$ C、 $\forall x \in R$ ， $x^{2} - 2 x + 1 \geq 0$ D、若P，A，B三点满足 $\vec{O P} = \frac{1}{4} \vec{O A} + \frac{3}{4} \vec{O B}$ ，则P，A，B三点共线

查看试题解析
10. 已知向量 $\vec{a} = (- 2 c o s^{2} x ， s i n^{2} x - f (x))$ ， $\vec{b} = (1 ， - \frac{1}{2})$ ，若 $\vec{a}$ 与 $\vec{b}$ 共线，则下列说法正确的是（）

A、函数 $f (x)$ 的最小正周期为 $π$ B、函数 $f (x)$ 在 $(\frac{π}{2} ， π)$ 上单调递增 C、直线 $x = \frac{π}{2}$ 是 $f (x)$ 图象的一条对称轴 D、将 $f (x)$ 的图像向左平移 $\frac{π}{4}$ 个单位得到函数 $y = s i n 2 x$ 的图象

查看试题解析
11. 已知等差数列 ${a_{n}}$ 的公差为d，前n项和为 $S_{n}$ ，若 $S_{8} = S_{12}$ ，则下列说法中正确的有（）

A、当 $n = 20$ 时， $S_{n} = 0$ B、当 $n = 10$ 时， $S_{n}$ 取得最大值 C、当 $d > 0$ 时， $a_{9} + a_{13} > 0$ D、当 $d < 0$ 时， $| a_{10} | > | a_{12} |$

查看试题解析
12. 对于函数 $f (x) = \frac{\ln x}{x^{2}}$ ，下列说法正确的是（）

A、 $f (x)$ 在 $x = \sqrt{e}$ 处取得极大值 $\frac{1}{2 e}$ B、 $f (x)$ 有两个不同的零点 C、 $f (\sqrt{2}) < f (\sqrt{π}) < f (\sqrt{3})$ D、若 $f (x) < k - \frac{1}{x^{2}}$ 在 $(0, + \infty)$ 上恒成立，则 $k > \frac{e}{2}$

查看试题解析

三、填空题

13. 已知向量 $\vec{a} = (1, 2)$ ， $\vec{b} = (4, - 7)$ ，若 $\vec{a} // \vec{c}$ ， $\vec{a} ⊥ (\vec{b} + \vec{c})$ ，则 $| \vec{c} | =$ ．

查看试题解析
14. 设 $x = θ$ 是函数 $f (x) = 3 c o s x + s i n x$ 的一个极值点，则 $c o s 2 θ - s i n^{2} θ =$ .

查看试题解析
15. 设 $△ A B C$ 的内角A，B，C所对边的长分别为a，b，c，若 $\frac{s i n B}{s i n A} = \frac{3}{5}$ ，且b，a，c成等差数列，则角 $C =$ ．

查看试题解析
16. 已知函数 $f (x) = x^{2} + 3 x + 1$ ， $g (x) = e^{x}$ ，若关于 $x$ 的不等式 $f (x) < m g (x)$ 的解集中恰好有一个整数，则实数 $m$ 的取值范围是.

查看试题解析

四、解答题

17. 已知函数 $f (x) = (\sqrt{3} \sin ω x + \cos ω x) \cos ω x - a (ω > 0)$ 的最小正周期为 $4 π$ ，最大值为1

(1)、求 $ω$ ， $a$ 的值，并求 $f (x)$ 的单调递增区间；

(2)、将 $f (x)$ 图象上所有点的纵坐标不变，横坐标缩短为原来的 $\frac{1}{2}$ 倍，再将得到的图象上所有点向右平移 $\frac{π}{4}$ 个单位，得到 $g (x)$ 的图象．若 $x \in (0, π)$ ，求满足 $g (x) \geq \frac{\sqrt{3}}{2}$ 的 $x$ 的取值范围．

查看试题解析
18. 已知 $S_{n}$ 为数列 ${a_{n}}$ 的前 $n$ 项和， $a_{1} = 2$ ， $7 S_{n} + 2 = a_{n + 1}$ ， $b_{n} = \frac{1}{\log_{2} a_{n} \cdot \log_{2} a_{n + 1}}$ ， $T_{n}$ 为数列 ${b_{n}}$ 的前 $n$ 项和.

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若 $m > 2022 T_{n}$ 对所有 $n \in N^{*}$ 恒成立，求满足条件 $m$ 的最小整数值.

查看试题解析
19. 已知函数 $f (x) = - \frac{1}{3} x^{3} + a x^{2} + b x + a b$ .

(1)、若 $f (x)$ 是奇函数，且有3个零点，求 $b$ 的取值范围；

(2)、若 $f (x)$ 在 $x = 1$ 处有极大值 $- \frac{22}{3}$ ，求当 $x \in [- 1 ， 3]$ 时 $f (x)$ 的值域.

查看试题解析
20. 如图，在平面直角坐标系中，三个向量 $\vec{O A}$ ， $\vec{O B}$ ， $\vec{O C}$ 满足条件： $| \vec{O A} | = 2 | \vec{O B} | = 2 | \vec{O C} | = 2$ ， $\vec{O A}$ 与 $\vec{O C}$ 的夹角为 $α$ ，且 $t a n α = 2$ ， $\vec{O B}$ 与 $\vec{O C}$ 的夹角为45°．

(1)、求点A，B，C的坐标；

(2)、若点P为线段OC上的动点，当 $\vec{P O} \cdot \vec{P A}$ 取得最小值时，求点P的坐标．

查看试题解析
21. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，且 $S_{n} = 2 a_{n} - 2$ ．

(1)、求 ${a_{n}}$ 的通项公式；

(2)、在 $a_{n}$ 与 $a_{n + 1}$ 之间插入 $n$ 个数，使这 $n + 2$ 个数组成一个公差为 $d_{n}$ 的等差数列，在数列 ${d_{n}}$ 中是否存在3项 $d_{m}$ ， $d_{k}$ ， $d_{p}$ （其中 $m$ ， $k$ ， $p$ 成等差数列）成等比数列？若存在，求出这样的3项；若不存在，请说明理由．

查看试题解析
22. 已知函数 $f (x) = l n x - m x + 1$ ， $g (x) = x (e^{x} - 2)$ .

(1)、若 $f (x)$ 的最大值是1，求 $m$ 的值；

(2)、若对其定义域内任意 $x$ ， $f (x) \leq g (x)$ 恒成立，求 $m$ 的取值范围.

查看试题解析