安徽省合肥市六校联盟2022-2023学年高二上学期数学期中联考试卷

试卷更新日期：2022-12-22 类型：期中考试

进入出卷网下载

一、单选题

1. 过 $A (- 2 ， - 3)$ ， $B (1 ， 0)$ 两点的直线的倾斜角是（）

A、45° B、60° C、120° D、135°

查看试题解析
2. 如图，在四面体OABC中， $\vec{O A} = \vec{a}$ ， $\vec{O B} = \vec{b}$ ， $\vec{O C} = \vec{c}$ .点M在OA上，且 $O M = 2 M A$ ， $N$ 为BC中点，则 $\vec{M N}$ 等于（）

A、 $\frac{1}{2} \vec{a} - \frac{2}{3} \vec{b} + \frac{1}{2} \vec{c}$ B、 $- \frac{2}{3} \vec{a} + \frac{1}{2} \vec{b} + \frac{1}{2} \vec{c}$ C、 $\frac{1}{2} \vec{a} + \frac{1}{2} \vec{b} - \frac{1}{2} \vec{c}$ D、 $\frac{2}{3} \vec{a} + \frac{2}{3} \vec{b} - \frac{1}{2} \vec{c}$

查看试题解析
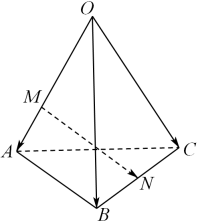3. 已知方程 $x^{2} + y^{2} - 2 x + 2 + k = 0$ 表示圆，则k的取值范围是（）

A、 $(- \infty ， - 1) \cup (3 ， + \infty)$ B、 $(- \infty ， - \frac{1}{3})$ C、 $(- \infty ， - 1)$ D、 $(- \frac{3}{2} ， + \infty)$

查看试题解析
4. 椭圆 $\frac{x^{2}}{m^{2} + 1} + \frac{y^{2}}{m^{2}} = 1$ $(m > 0)$ 的焦点为 $F_{1}$ ， $F_{2}$ ，与y轴的一个交点为A，若 $∠ F_{1} A F_{2} = \frac{π}{2}$ ，则m=（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

查看试题解析
5. 如图，ABCD－EFGH是棱长为1的正方体，若P在正方体内部且满足 $\vec{A P} = \frac{3}{5} \vec{A B} + \frac{1}{2} \vec{A D} + \frac{2}{3} \vec{A E}$ ，则P到AB的距离为（）

A、 $\frac{3}{4}$ B、 $\frac{4}{5}$ C、 $\frac{3}{5}$ D、 $\frac{5}{6}$

查看试题解析
6. 如图，在四棱锥P－ABCD中，底面ABCD是边长为1的正方形，侧棱PA的长为1，且PA与AB，AD的夹角都等于60°.若M是PC的中点，则 $| \vec{B M} | =$ （）

A、 $\frac{3}{4}$ B、 $\frac{\sqrt{3}}{4}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
7. 已知点P在直线l： $x + y - 10 = 0$ 上，过点P的两条直线与圆O： $x^{2} + y^{2} = 8$ 分别相切于A，B两点，则圆心O到直线AB的距离的最大值为（）

A、 $\frac{\sqrt{10}}{2}$ B、 $\sqrt{5}$ C、 $\frac{4 \sqrt{2}}{5}$ D、 $\sqrt{2}$

查看试题解析
8. 国家体育场“鸟巢”的钢结构鸟瞰图如图1所示，内外两圈的钢骨架是离心率相同的椭圆；某校体育馆的钢结构与“鸟巢”相同，其平面图如图2所示，若由外层椭圆长轴一端点A和短轴一端点B分别向内层椭圆引切线AC，BD，且两切线斜率之积等于 $- \frac{1}{3}$ ，则椭圆的离心率为（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{6}}{3}$

查看试题解析

二、多选题

9. 下列说法正确的是（）

A、已知 $\vec{n}$ 为平面α的一个法向量， $\vec{m}$ 为直线l的一个方向向量，若 $〈 \vec{n} ， \vec{m} 〉 = \frac{2 π}{3}$ ，则l与α所成角为 $\frac{π}{6}$ B、P、A、B、C是空间中四点，若 $\vec{O A} + \vec{O B} + \vec{O C} = 3 \vec{O P}$ ，则P、A、B、C四点共面 C、过 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ 两点的直线方程为 $\frac{y - y_{1}}{y_{2} - y_{1}} = \frac{x - x_{1}}{x_{2} - x_{1}}$ D、“ $a b = 8$ ”的一个必要不充分条件是“直线 $2 x + a y - 1 = 0$ 与直线 $b x + 4 y - 2 = 0$ 平行”

查看试题解析
10. 下列说法错误的是（）

A、 $\vec{a} = (1 ， - 1)$ 是直线 $x + y - 3 = 0$ 的一个单位方向向量 B、直线 $x + 2 y - 4 = 0$ 与直线 $2 x + 4 y + 1 = 0$ 之间的距离是 $\frac{9 \sqrt{5}}{10}$ C、点 $A (2 ， 1)$ 到直线l： $x - y + 2 = 0$ 的距离为 $\frac{3}{2}$ D、经过点 $P (3 ， 4)$ ，且在两坐标轴上的截距的绝对值相等的直线条数共有2条

查看试题解析
11. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左，右焦点分别为 $F_{1} ， F_{2}$ ，长轴长为4，点 $P (\sqrt{2} ， 1)$ 在椭圆 $C$ 外，点 $Q$ 在椭圆 $C$ 上，则（）

A、椭圆 $C$ 的离心率的取值范围是 $(\frac{\sqrt{2}}{2} ， 1)$ B、当椭圆 $C$ 的离心率为 $\frac{\sqrt{3}}{2}$ 时， $| Q F_{1} |$ 的取值范围是 $[2 - \sqrt{3} ， 2 + \sqrt{3}]$ C、存在点 $Q$ 使得 ${\vec{Q F}}_{1} \cdot \vec{Q F_{2}} = 0$ D、 $\frac{1}{| Q F_{1} |} + \frac{1}{| Q F_{2} |}$ 的最小值为2

查看试题解析
12. 如下图，正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $M$ 为线段 $C C_{1}$ 上的动点， $A M ⊥$ 平面 $α$ ，则下面说法正确的是（）

A、直线 $A B$ 与平面 $α$ 所成角的正弦值范围为 $[\frac{\sqrt{3}}{3} ， \frac{\sqrt{2}}{2}]$ B、已知 $N$ 为 $D D_{1}$ 中点，当 $A M + M N$ 的和最小时， $\frac{M C}{D N} = 2 - \sqrt{2}$ C、点 $M$ 为 $C C_{1}$ 的中点时，若平面 $α$ 经过点 $B$ ，则平面 $α$ 截正方体所得截面图形是等腰梯形 D、点 $M$ 与点 $C_{1}$ 重合时，平面 $α$ 截正方体所得的截面，其面积越大，周长就越大.

查看试题解析

三、填空题

13. 已知圆 $C_{1} ： x^{2} + {(y - a)}^{2} = 9$ 与圆 $C_{2} ： {(x - a)}^{2} + y^{2} = 1$ 有四条公切线，写出一个实数a的可能取值是．

查看试题解析
14. 向量 $\vec{a} = (1 ， 0 ， 1)$ ， $\vec{b} = (x ， 1 ， 2)$ ，且 $\vec{a} \cdot \vec{b} = 3$ ，则向量 $\vec{b}$ 在 $\vec{a}$ 上的投影向量的坐标为．

查看试题解析
15. 已知圆 $C ： x^{2} + y^{2} = 4$ ，直线 $l ： y = x + b$ .若圆 $C$ 上恰有三个点到直线 $l$ 的距离等于1，则 $b$ 的值为.

查看试题解析
16. 已知椭圆C： $\frac{x^{2}}{4} + y^{2} = 1$ 的左､右焦点分别是 $F_{1}$ ， $F_{2}$ ，过点 $F_{1}$ 的直线交椭圆于A，B两点，则 $△ A B F_{2}$ 的内切圆面积的最大值为.

查看试题解析

四、解答题

17. 已知点 $A (0 ， 1)$ ， ____，从条件①、条件②、条件③中选择一个作为已知条件补充在横线处，并作答．
条件①：点 $A$ 关于直线 $l_{1}$ 的对称点 $B$ 的坐标为 $(2 ， - 1)$ ；
条件②：点 $B$ 的坐标为 $(2 ， - 1)$ ，直线 $l_{1}$ 过点 $(2 ， 1)$ 且与直线 $A B$ 垂直；
条件③点 $C$ 的坐标为 $(2 ， 3)$ ，直线 $l_{1}$ 过点 $(2 ， 1)$ 且与直线 $A C$ 平行．
注：如果选择多个条件分别解答，按第一个解答计分．

(1)、求直线 $l_{1}$ 的方程；

(2)、求直线 $l_{2}$ ： $x - 2 y + 2 = 0$ 关于直线 $l_{1}$ 的对称直线的方程．

查看试题解析
18. 如图，在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A C ⊥ B C ， A C = B C = 2 ， C C_{1} = 3$ ，点 $D ， E$ 分别在棱 $A A_{1}$ 和棱 $C C_{1}$ 上，且 $A D = 1 ， C E = 2$ ．

(1)、设 $F$ 为 $B_{1} C_{1}$ 中点，求证： $A_{1} F / /$ 平面 $B D E$ ；

(2)、求直线 $A_{1} B_{1}$ 与平面 $B D E$ 所成角的正弦值．

查看试题解析
19. 已知圆 $C$ 的圆心为原点，且与直线 $3 x + 4 y - 10 = 0$ 相切，直线 $l$ 过点 $M (1 ， 2)$ .

(1)、若直线 $l$ 与圆 $C$ 相切，求直线 $l$ 的方程；

(2)、若直线 $l$ 被圆 $C$ 所截得的弦长为 $2 \sqrt{3}$ ，求直线 $l$ 的方程.

查看试题解析
20. 已知椭圆 $C ： \frac{x^{2}}{4} + \frac{y^{2}}{b^{2}} = 1 (2 > b > 0)$ ，直线 $y = x$ 被椭圆 $C$ 截得的线段长为 $\frac{4 \sqrt{10}}{5}$ .

(1)、求椭圆 $C$ 的标准方程；

(2)、过椭圆 $C$ 的右顶点作互相垂直的两条直线 $l_{1} ， l_{2}$ .分别交椭圆 $C$ 于 $M ， N$ 两点（点 $M ， N$ 不同于椭圆 $C$ 的右顶点），证明：直线 $M N$ 过定点.

查看试题解析
21. 如下图，在四棱锥 $P - A B C D$ 中，已知 $P A ⊥$ 平面 $A B C D$ ，且四边形 $A B C D$ 为直角梯形， $∠ A B C = ∠ B A D = \frac{π}{2}$ ， $P A = A D = 2$ ， $A B = B C = 1$ ．

(1)、求平面 $P A B$ 与平面 $P C D$ 夹角的余弦值；

(2)、定义：两条异面直线之间的距离是指其中一条直线上任意一点到另一条直线距离的最小值，利用此定义求异面直线 $P B$ 与 $C D$ 之间的距离．

查看试题解析
22. 如图，已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右顶点分别是 $A ， B$ ，且经过点 $(1 ， - \frac{\sqrt{3}}{2})$ ，直线 $l ： x = t y - 1$ 恒过定点 $F$ 且交椭圆于 $D ， E$ 两点， $F$ 为 $O A$ 的中点.

(1)、求椭圆 $C$ 的标准方程；

(2)、记 $△ B D E$ 的面积为S，求S的最大值.

查看试题解析