山东省淄博市张店区2022-2023学年八年级上学期期中数学试题

试卷更新日期：2022-12-20 类型：期中考试

进入出卷网下载

一、单选题

1. 若分式 $\frac{3}{x + 5}$ 有意义，则x的取值范围为（）

A、 $x \neq - 5$ B、 $x \neq 0$ C、 $x \neq 5$ D、 $x > - 5$

查看试题解析
2. 下列各式从左到右的变形是因式分解的是（）

A、 $6 x^{2} y = 6 x y \cdot x$ B、 $4 (x + 2) = 4 x + 8$ C、 $x^{2} - 2 x - 5 = x (x - 2) - 5$ D、 $a^{2} - 1 = (a + 1) (a - 1)$

查看试题解析
3. 分式 $\frac{1}{x^{2} + 5 x}$ 与 $\frac{1}{x^{2} - 25}$ 的最简公分母是（）

A、 $x (x + 5)$ B、 $(x + 5) (x - 5)$ C、 $x (x - 5)$ D、 $x (x + 5) (x - 5)$

查看试题解析
4. 如图是甲、乙两人6次投篮测试（每次投篮10个）成绩的统计图，甲、乙两人测试成绩方差分别记作 ${S_{甲}}^{2}$ ， ${S_{乙}}^{2}$ ，则下列结论正确的是（）

A、 ${S_{甲}}^{2} < {S_{乙}}^{2}$ B、 ${S_{甲}}^{2} > {S_{乙}}^{2}$ C、 ${S_{甲}}^{2} = {S_{乙}}^{2}$ D、无法确定

查看试题解析
5.
如图，边长为a，b的矩形的周长为14，面积为10，则a²b+ab²的值为（　　）

A、140 B、70 C、35 D、24

查看试题解析
6. 下列各式从左到右的变形正确的是（）

A、 $\frac{- x - y}{x} = - \frac{x - y}{x}$ B、 $\frac{a + b}{a - b} = \frac{a - b}{a + b}$ C、 $\frac{0.2 a + b}{0.2 b} = \frac{2 a + b}{2 b}$ D、 $\frac{x - \frac{1}{2} y}{y} = \frac{2 x - y}{2 y}$

查看试题解析
7. 将几个图形拼成一个新的图形，再通过两种不同的方法计算同一个图形的面积，可以得到一个等式．例如，由图（1）可得等式： $x^{2} + (p + q) x + p q = (x + p) (x + q)$ ．将图（2）所示的卡片若干张进行拼图，可以将二次三项式 $a^{2} + 3 a b + 2 b^{2}$ 分解因式为（）

A、 $(a + b) (2 a + b)$ B、 $(a + b) (3 a + b)$ C、 $(a + b) (a + 2 b)$ D、 $(a + b) (a + 3 b)$

查看试题解析
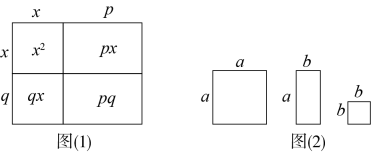8. 甲、乙两人分两次在同一粮店内买粮食，两次的单价不同，甲每次购粮100千克，乙每次购粮100元．若规定：谁两次购粮的平均单价低，谁的购粮方式就合算．那么这两次购粮（）

A、甲合算 B、乙合算 C、甲、乙一样 D、无法确定

查看试题解析
9. 篮子里有若干苹果，可以平均分给 $(x + 1)$ 名同学，也可以平均分给 $(x - 3)$ 名同学（x为大于3的正整数），用代数式表示苹果数量不可能的是（）

A、 $2 x^{3} - 4 x^{2} - 6 x$ B、 $x^{3} - 2 x - 3$ C、 $3 (x + 1) (x - 3)$ D、 $x (x^{2} - 2 x - 3)$

查看试题解析
10. 若关于x的分式方程 $\frac{x}{x - 3} = 1 + \frac{m x - 2}{9 - x^{2}}$ 无解，则m的值为（）

A、-3或 $- \frac{16}{3}$ B、 $- \frac{16}{3}$ 或 $- \frac{2}{3}$ C、-3或 $- \frac{16}{3}$ 或 $- \frac{2}{3}$ D、-3或 $- \frac{2}{3}$

查看试题解析

二、填空题

11. 当x=时，分式 $\frac{x^{2} - 1}{x - 1}$ 值为0．

查看试题解析
12. 分解因式： $2 x^{2} y - 4 x y + 2 y =$ ．

查看试题解析
13. 若关于x的方程 $\frac{1}{x - 1} + \frac{2 x + m}{1 - x} = 1$ 有增根，则m的值是．

查看试题解析
14. 为了解学生的睡眠状况，调查了一个班50名学生每天的睡眠时间，绘成睡眠时间条形统计图（如图所示），则所调查学生睡眠时间的众数和中位数分别为和．

查看试题解析
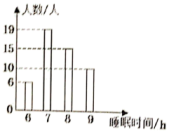15. 通过对《分式与分式方程》一章的学习，我们知道用分式方程解决实际问题的一般步骤：
请根据所给分式方程 $\frac{1400}{x} - \frac{1400}{2.8 x} = 9$ ，联系生活实际，编写一个能通过列出此分式方程进行解决的实际问题：．（要求题目完整，题意清楚，不要求解方程）

查看试题解析

三、解答题

16. 先化简 $(\frac{1}{x + 2} + 1) \div \frac{x^{2} + 6 x + 9}{x^{2} - 4}$ ，然后再从 $- 3$ ， $- 2$ ， 0，2，3中选一个合适的数作为x的值代入求值．

查看试题解析
17. 解方程：

(1)、 $\frac{3}{x - 1} = \frac{4}{x}$

(2)、 $\frac{1}{x - 2} + 3 = \frac{1 - x}{2 - x}$

查看试题解析
18. 某校为了提升初中学生学习数学的兴趣，举办“玩转数学”比赛．现有甲、乙两个小组进入决赛，评委从准备工作、研究报告、小组展示、答辩四个方面为各小组打分，各项成绩均按百分制记录，甲、乙两个小组各项得分如下表：
小组
准备工作
研究报告
小组展示
答辩
甲
85
78
85
73
乙
73
80
82
83

(1)、计算各小组的平均成绩，哪个小组的成绩高？

(2)、如果按2：1：3：4的比来计算，求各小组的成绩，哪个小组的成绩高？

查看试题解析
19. 阅读下列材料：
常用的分解因式方法有提公因式、公式法等．但有的多项式只用上述方法就无法分解，如 $x^{2} - 4 y^{2} + 2 x - 4 y$ ，细心观察这个式子会发现前两项符合平方差公式，后两项可提取公因式，分解过程为：
$x^{2} - 4 y^{2} + 2 x - 4 y$
$= (x^{2} - 4 y^{2}) + (2 x - 4 y)$ 分组
$= (x - 2 y) (x + 2 y) + 2 (x - 2 y)$ 组内分解因式
$= (x - 2 y) (x + 2 y + 2)$ 整体思想提公因式
这种分解因式的方法叫分组分解法，利用这种方法解决下列问题：

(1)、分解因式： $9 x^{2} - 9 x + 3 y - y^{2}$ ；

(2)、已知 $△ A B C$ 的三边 $a 、 b 、 c$ 满足 $a^{2} - b^{2} - a c + b c = 0$ ，判断 $△ A B C$ 的形状并说明理由．

查看试题解析
20. 某中学在党的二十大胜利召开之际，举行“同声放歌心向党，携手欢庆二十大”唱红歌大赛，向党的二十大献礼，信心满怀向未来．八年级和九年级根据级部初赛成绩，各选出5名选手参加复赛，两个年级各选出的5名选手的复赛成绩如图所示．
年级
平均数（分）
中位数
众数
八年级
85
a
85
九年级
85
80
b

(1)、根据图示填写上表中的 $a =$ ， $b =$ ；

(2)、结合两个年级复赛成绩的平均数和中位数，分析哪个年级的复赛成绩较好；

(3)、计算两个年级复赛成绩的方差，并说明哪个年级的成绩较稳定．

查看试题解析
21. 乘法公式的探究及应用．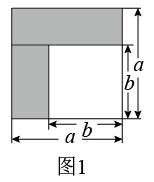

(1)、如图1，若将阴影部分裁剪下来，重新拼成一个矩形，如图2，通过比较图1、图2阴影部分的面积，可以得到整式乘法公式：；

(2)、2¹⁶-1可以被10和20之间某两个整数整除，则这两个数分别为．

(3)、计算： $2 \times (3 + 1) (3^{2} + 1) (3^{4} + 1) (3^{8} + 1) (3^{16} + 1) + 1$ ．

查看试题解析
22. 【阅读学习】阅读下面的解题过程：
已知： $\frac{x}{x^{2} + 1} = \frac{1}{3}$ ，求 $\frac{x^{2}}{x^{4} + 1}$ 的值．
解：由 $\frac{x}{x^{2} + 1} = \frac{1}{3}$ 知 $x \neq 0$ ，所以 $\frac{x^{2} + 1}{x} = 3$ ，即 $x + \frac{1}{x} = 3$ ，
所以 $\frac{x^{4} + 1}{x^{2}} = x^{2} + \frac{1}{x^{2}} = {(x + \frac{1}{x})}^{2} - 2 = 3^{2} - 2 = 7$ ，
故 $\frac{x^{2}}{x^{4} + 1}$ 的值为 $\frac{1}{7}$ ．

(1)、上题的解法叫做“倒数法”，请你利用“倒数法”解决下面的题目：
已知 $\frac{x}{x^{2} - 3 x + 1} = - 2$ ，求 $\frac{x^{2}}{x^{4} + 5 x^{2} + 1}$ 的值．

(2)、【拓展延伸】
已知 $\frac{1}{a} + \frac{1}{b} = \frac{1}{2}$ ， $\frac{1}{b} + \frac{1}{c} = \frac{1}{3}$ ， $\frac{1}{a} + \frac{1}{c} = \frac{1}{5}$ ，求 $\frac{a b c}{a b + b c + a c}$ 的值．

查看试题解析
23. 为落实“数字中国”的建设工作，市政府计划对全市中小学多媒体教室进行安装改造，现安排两个安装公司共同完成．已知甲公司安装工效是乙公司安装工效的1.5倍，乙公司安装36间教室比甲公司安装同样数量的教室多用3天．

(1)、求甲、乙两个公司每天各安装多少间教室？

(2)、已知甲公司安装费每天800元，乙公司安装费每天400元，现需安装教室120间，若想尽快完成安装工作且安装总费用不超过15000元，则最多安排甲公司工作多少天？

查看试题解析

小组	准备工作	研究报告	小组展示	答辩
甲	85	78	85	73
乙	73	80	82	83

年级	平均数（分）	中位数	众数
八年级	85	a	85
九年级	85	80	b