山东省枣庄市薛城区2022-2023学年八年级上学期期中数学试题

试卷更新日期：2022-12-20 类型：期中考试

进入出卷网下载

一、单选题

1. 计算 $\sqrt{16}$ 的结果是（）

A、8 B、16 C、4 D、±4

查看试题解析
2. 第24届冬季奥林匹克运动会将于2022年由北京市和张家口市联合举行．以下能够准确表示张家口市地理位置的是（）

A、离北京市200千米 B、在河北省 C、在宁德市北方 D、东经114.8°，北纬40.8°

查看试题解析
3. 下列计算中，正确的是（）

A、 $\sqrt{3} + \sqrt{4} = \sqrt{7}$ B、 $\sqrt{3} \times \sqrt{5} = \sqrt{15}$ C、 $\sqrt{(- 2)^{2}} = - 2$ D、 $3 \sqrt{2} - \sqrt{2} = 3$

查看试题解析
4. 疫情期间，小颖宅家学习．一天，她在课间休息时，从窗户向外望，看到一人为快速从A处到达居住楼B处，直接从边长为24米的正方形草地中穿过．为保护草地，小颖计划在A处立一个标牌：“少走？米，踏之何忍”，已知B、C两处的距离为7米，那么标牌上？处的数字是（）

A、3 B、4 C、5 D、6

查看试题解析
5. 一块正方形的瓷砖边长为 $\sqrt{55} c m$ ，它的边长大约在（）

A、4cm-5cm之间 B、5cm-6cm之间 C、6cm-7cm之间 D、7cm-8cm之间

查看试题解析
6. 设点P（x，y）在第二象限，且|x|=5，|y|=2，则点P的坐标是（）

A、（-5，2） B、（5，2） C、（-5，-2） D、（5，-2）

查看试题解析
7. 如果P点的坐标为(a，b)，它关于y轴的对称点为P₁ ， P₁关于x轴的对称点为P₂ ，已知P₂的坐标为(－2，3)，则点P的坐标为（）

A、(－2，－3) B、(2，－3) C、(－2，3) D、(2，3)

查看试题解析
8. 如图，一只蚂蚁从正方体的下底面A点沿着侧面爬到上底面B点，正方体棱长为3cm，则蚂蚁所走过的最短路径是（）

A、3 $\sqrt{3}$ cm B、6cm C、3 $\sqrt{2}$ cm D、3 $\sqrt{5}$ cm

查看试题解析
9. 某市出租车计费办法如图所示．根据图象信息，下列说法错误的是（）

A、出租车起步价是10元 B、在3千米内只收起步价 C、超过3千米部分（x＞3）每千米收3元 D、超过3千米时（x＞3）所需费用y与x之间的函数关系式是y=2x+4

查看试题解析
10. 如图，在2×2的正方形网格中，每个小正方形边长为1，点A，B，C均为格点，以点A为圆心，AB长为半径作弧，交格线于点D，则CD的长为（）

A、 $\frac{1}{3}$ B、 $\sqrt{3}$ C、 $\sqrt{5} - 2$ D、 $2 - \sqrt{3}$

查看试题解析
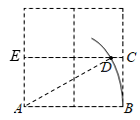11. 下列关于一次函数 y＝－x＋2 的图象性质的说法中，错误的是（）

A、直线与 x 轴交点的坐标是（0，2） B、直线经过第一、二、四象限 C、y 随 x 的增大而减小 D、与坐标轴围成的三角形面积为 2

查看试题解析
12. 如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离 $B C$ 为0.7米，梯子顶端到地面的距离 $A C$ 为2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，梯子顶端到地面的距离 $A^{'} D$ 为1.5米，则小巷的宽为（）

A、2.5米 B、2.6米 C、2.7米 D、2.8米

查看试题解析

二、填空题

13. 如果 $b = \sqrt{a - 3} + \sqrt{3 - a} + 6$ ，则 $\sqrt{a b} =$ ．

查看试题解析
14. 一次函数y=kx+b的图象与y=x+1的图象平行，且经过点(-3，4)，则这个函数的表达式为.

查看试题解析
15. 如图，赵爽弦图是由四个全等的直角三角形与一个小正方形拼成大正方形，若小正方形边长为1，大正方形边长为5，则一个直角三角形的周长是．

查看试题解析
16. 已知点A坐标为 $(1 ， 2)$ ，若直线 $A B / / y$ 轴，且 $A B = 5$ ，则点B坐标为．

查看试题解析
17. 如图所示，甲、乙两车在某时间段内速度随时间变化的图象．下列结论：
①甲的速度始终保持不变；

②乙车第12秒时的速度为32米/秒；

③乙车前4秒行驶的总路程为48米.

其中正确的是．（填序号）

查看试题解析
18. 在 $△ A B C$ 中， $A B = A C = 5$ ， $B C = 6$ .若点 P在边AC上移动，则线段BP的最小值是 .

查看试题解析

三、解答题

19. 正数x的两个平方根分别是 $2 - a, 2 a - 7$

(1)、求 $a$ 的值；

(2)、求 $1 - x$ 这个数的立方根；

查看试题解析
20. 计算

(1)、 $2 \sqrt{\frac{1}{3}} \times \sqrt{9} - \sqrt{12} + \sqrt[3]{\frac{7}{8} - 1}$

(2)、 $\sqrt{8} - (2020 - π)^{0} + 2 | 1 - \sqrt{2} | + (- 3)^{2}$

查看试题解析
21. 如图，四边形ABCD中， $∠ B = 90 °$ ， $B C = 2 \sqrt{3}$ ， $A B = 2$ ， $C D = 3$ ， $A D = 5$ ．

(1)、求证： $A C ⊥ C D$ ；

(2)、求四边形ABCD的面积．

查看试题解析
22. 如图，在平面直角坐标系中 $△ A B C$ 各顶点的坐标分别为 $A (4 ， 0)$ ， $B (- 1 ， 4)$ ， $C (- 3 ， 1)$ ．

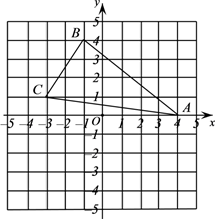(1)、若点P是x轴上的一动点，则 $P B + P C$ 的最小值是．

(2)、在图中作 $△ A^{'} B^{'} C^{'}$ ，使 $△ A^{'} B^{'} C^{'}$ 与 $△ A B C$ 关于y轴对称；

(3)、请分别写出点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 的坐标．

查看试题解析
23. 阅读下面的文字，解答问题： $\sqrt{2}$ 是一个无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分无法全部写出来，但是我们可以想办法把它表示出来因为 $1 < \sqrt{2} < 2$ ，所以 $\sqrt{2}$ 的整数部分为1，将 $\sqrt{2}$ 减去其整数部分后，得到的差就是小数部分，于是 $\sqrt{2}$ 的小数部分为 $\sqrt{2} - 1$ ．请解答下列问题：

(1)、 $\sqrt{5}$ 的整数部分是，小数部分是；

(2)、如果 $7 + \sqrt{10}$ 的小数部分为a， $7 - \sqrt{10}$ 的小数部分为b，若 $(x + 1)^{2} = a + b$ ，求x的值．

查看试题解析
24. 如图，已知直线 $y = - \frac{1}{3} x + 1$ 与x轴、y轴分别交于A、B两点，以线段AB为直角边在第一象限内作等腰 $R t △ A B C$ ， $∠ B A C = 90 °$ ．

(1)、A点坐标为， B点坐标为；

(2)、求直线BC的解析式；

(3)、点P为直线BC上一个动点，当 $S_{△ A O P} = 3 S_{△ A O B}$ 时，求点P坐标．

查看试题解析
25. 小明在解决问题：已知 $a = \frac{1}{2 + \sqrt{3}}$ ，求 $2 a^{2} - 8 a + 1$ 的值，他是这样分析与解答的：
$∵ a = \frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$ ，
$∴ a = 2 - \sqrt{3}$ ，
$∴ a - 2 = - \sqrt{3}$ ，
$∴ (a - 2)^{2} = 3$ ，
$∴ a^{2} - 4 a + 4 = 3$ ， $∴ a^{2} - 4 a = - 1$ ，
$∴ 2 a^{2} - 8 a + 1 = 2 (a^{2} - 4 a) + 1 = 2 \times (- 1) + 1 = - 1$ ．
请你认真审视小明的解答过程，根据他的做法解决下列问题：

(1)、计算 $\frac{1}{\sqrt{n + 1} + \sqrt{n}} =$ ；

(2)、计算 $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \dots + \frac{1}{\sqrt{2020} + \sqrt{2019}}$ （写出计算过程）；

(3)、如果 $a = \frac{1}{\sqrt{5} - 2}$ ，求 $2 a^{2} - 8 a + 1$ 的值．

查看试题解析