山东省日照市五莲县2022-2023学年八年级上学期期中数学试题
试卷更新日期:2022-12-20 类型:期中考试
一、单选题
-
1. 自新冠肺炎疫情发生以来,全国人民共同抗疫,咸宁市积极普及科学防控知识,下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一副三角板如图叠放在一起,则图中∠α的度数为( )
2. 一副三角板如图叠放在一起,则图中∠α的度数为( ) A、35° B、30° C、25° D、15°3. 已知等腰三角形的两边长分别为4cm、8cm,则该等腰三角形的周长是( )A、12cm B、16cm C、16cm或20cm D、20cm4. 下列说法正确的是( )A、三角形三条高交于三角形内一点 B、一个钝角三角形一定不是等腰三角形,也不是等边三角形 C、有两条边及其中一条边的对角对应相等的两个三角形全等 D、平面上两个全等的图形不一定关于某直线对称5. 已知点A(2,3)和点B(4,1),在坐标轴上有一点P到点A和点B的距离相等,则点P的坐标为( )A、(1,0) B、(0,-1) C、(1,0) 或 (0,-1) D、(2,0)或(0,-1)6. 中, , 中线 , 则边的取值范围是( )A、 B、 C、 D、7. 如图,BE,CF是△ABC的角平分线,∠ABC=80°,∠ACB=60°,EB,CF相交于D,则∠CDE的度数是( )
A、35° B、30° C、25° D、15°3. 已知等腰三角形的两边长分别为4cm、8cm,则该等腰三角形的周长是( )A、12cm B、16cm C、16cm或20cm D、20cm4. 下列说法正确的是( )A、三角形三条高交于三角形内一点 B、一个钝角三角形一定不是等腰三角形,也不是等边三角形 C、有两条边及其中一条边的对角对应相等的两个三角形全等 D、平面上两个全等的图形不一定关于某直线对称5. 已知点A(2,3)和点B(4,1),在坐标轴上有一点P到点A和点B的距离相等,则点P的坐标为( )A、(1,0) B、(0,-1) C、(1,0) 或 (0,-1) D、(2,0)或(0,-1)6. 中, , 中线 , 则边的取值范围是( )A、 B、 C、 D、7. 如图,BE,CF是△ABC的角平分线,∠ABC=80°,∠ACB=60°,EB,CF相交于D,则∠CDE的度数是( ) A、130° B、70° C、80° D、75°8. 如图,在△ABC中,∠C=90°,按以下步骤作图:①以点A为圆心、适当长为半径作圆弧,分别交边AC,AB于点M、N;②分别以点M和点N为圆心、大于 MN的长为半径作圆弧,在∠BAC内,两弧交于点P;③作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A、130° B、70° C、80° D、75°8. 如图,在△ABC中,∠C=90°,按以下步骤作图:①以点A为圆心、适当长为半径作圆弧,分别交边AC,AB于点M、N;②分别以点M和点N为圆心、大于 MN的长为半径作圆弧,在∠BAC内,两弧交于点P;③作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A、15 B、30 C、45 D、609. 如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )
A、15 B、30 C、45 D、609. 如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( ) A、3 B、4 C、6 D、810. 如图,△ 是等边三角形, 为 的中点, ,垂足为点 , ∥ , ,下列结论错误的是( )
A、3 B、4 C、6 D、810. 如图,△ 是等边三角形, 为 的中点, ,垂足为点 , ∥ , ,下列结论错误的是( )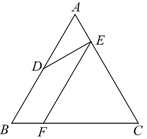 A、 30° B、 C、△ 的周长为10 D、△ 的周长为911. 如图,等边的边长为4,是边上的中线,是边上的动点,是边上一点,若 , 当取得最小值时,则的度数为( )
A、 30° B、 C、△ 的周长为10 D、△ 的周长为911. 如图,等边的边长为4,是边上的中线,是边上的动点,是边上一点,若 , 当取得最小值时,则的度数为( ) A、 B、 C、 D、12. 如图,已知 和 都是等边三角形,且 、 、 三点共线. 与 交于点 , 与 交于点 , 与 交于点 ,连结 .以下五个结论:① ;② ;③ ;④ 是等边三角形;⑤ .其中正确结论的有( )个
A、 B、 C、 D、12. 如图,已知 和 都是等边三角形,且 、 、 三点共线. 与 交于点 , 与 交于点 , 与 交于点 ,连结 .以下五个结论:① ;② ;③ ;④ 是等边三角形;⑤ .其中正确结论的有( )个 A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、填空题
-
13. 一个多边形截去一个角后,形成新多边形的内角和为 , 则原多边形边数为;其中边数最少的原多边形从一顶点出发,能做条对角线.14. 科技馆为某机器人编制了一个程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为米.
 15. 当三角形中一个内角α是另一个内角β的一半时,我们称此三角形为“半角三角形”,其中α称为“半角”.如果一个“半角三角形”的“半角”为20°,那么这个“半角三角形”的最大内角的度数为 .16. 在平面直角坐标系中,点A的坐标为 , 点B的坐标为 , 点C的坐标为 , 如果要使与全等,那么点D的坐标是 .
15. 当三角形中一个内角α是另一个内角β的一半时,我们称此三角形为“半角三角形”,其中α称为“半角”.如果一个“半角三角形”的“半角”为20°,那么这个“半角三角形”的最大内角的度数为 .16. 在平面直角坐标系中,点A的坐标为 , 点B的坐标为 , 点C的坐标为 , 如果要使与全等,那么点D的坐标是 .三、解答题
-
17.(1)、作图题:(不写作法,但必须保留作图痕迹)
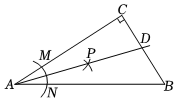
如图:某地有两所大学和两条相交叉的公路,(点M,N表示大学,AO,BO表示公路).现计划修建一座物资仓库.希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库P应该建在什么位置吗?在所给的图形中画出你的设计方案.
 (2)、如图,在 , CD是AB边上高,BE为角平分线,若 , 求的度数.
(2)、如图,在 , CD是AB边上高,BE为角平分线,若 , 求的度数. 18. 如图所示,已知 AD//BC, 点 E 为 CD 上一点,AE、BE 分别平分∠DAB、∠CBA,BE交 AD 的延长线于点 F.求证:
18. 如图所示,已知 AD//BC, 点 E 为 CD 上一点,AE、BE 分别平分∠DAB、∠CBA,BE交 AD 的延长线于点 F.求证: (1)、△ABE≌△AEF;(2)、 AD+BC=AB19. 如图,在平面直角坐标系中,A(-3,2),B(-4,-3),C(-1,-1).
(1)、△ABE≌△AEF;(2)、 AD+BC=AB19. 如图,在平面直角坐标系中,A(-3,2),B(-4,-3),C(-1,-1).
⑴在图中作出△ABC关于y轴对称的△A1B1C1;
⑵写出点△A1 , B1 , C1的坐标(直接写答案):A1 ▲ ;B1 ▲ ;C1 ▲ ;
⑶△A1B1C1的面积为 ▲ ;
⑷在y轴上画出点P,使PB+PC最小.
20. 如图,在中,边的垂直平分线分别交于D、E. (1)、若 , 求的周长;(2)、若 , 求的度数.21. 已知如图,中, , , D为的中点, , 垂足为E,过点B作 , 交DE的延长线于点F,连接交于点G.探究和有什么数量关系和位置关系?并证明你的猜想.
(1)、若 , 求的周长;(2)、若 , 求的度数.21. 已知如图,中, , , D为的中点, , 垂足为E,过点B作 , 交DE的延长线于点F,连接交于点G.探究和有什么数量关系和位置关系?并证明你的猜想. 22. 在 中,AB=20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以 cm/s( >0且 )的速度从C点出发在线段CA上运动,设运动时间为 秒。
22. 在 中,AB=20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以 cm/s( >0且 )的速度从C点出发在线段CA上运动,设运动时间为 秒。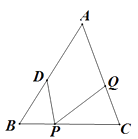 (1)、若AB=AC,P在线段BC上,求当 为何值时,能够使 和 全等?
(1)、若AB=AC,P在线段BC上,求当 为何值时,能够使 和 全等?
(2)、若 ,求出发几秒后, 为直角三角形?
(3)、若 ,当 的度数为多少时, 为等腰三角形?(请直接写出答案,不必写出过程)