山东省聊城市临清市2022-2023学年八年级上学期期中数学试题
试卷更新日期:2022-12-20 类型:期中考试
一、单选题
-
1. “致中和,天地位焉,万物育焉.”中国古人把和谐平衡的精神之美,演变成了一种对称美.从古至今,人们将对称元素赋予建筑、器物、绘画、饰品等事物上,使对称之美惊艳了千年的时光.在下列我国建筑简图中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在平面直角坐标系中,点关于x轴对称的点的坐标是( )A、 B、 C、 D、3. 下列代数式中是分式的为( )A、 B、 C、 D、4. 若分式有意义,则x的取值范围是( )A、x=2 B、x>2 C、x<2 D、x≠25. 如图, , , 则的度数为( )
2. 在平面直角坐标系中,点关于x轴对称的点的坐标是( )A、 B、 C、 D、3. 下列代数式中是分式的为( )A、 B、 C、 D、4. 若分式有意义,则x的取值范围是( )A、x=2 B、x>2 C、x<2 D、x≠25. 如图, , , 则的度数为( ) A、 B、 C、 D、6. 下列式子从左到右变形一定正确的是( )A、 B、 C、 D、7. 如图,AC是△ABC和△ADC的公共边,下列条件中不能判定△ABC≌△ADC的是( )
A、 B、 C、 D、6. 下列式子从左到右变形一定正确的是( )A、 B、 C、 D、7. 如图,AC是△ABC和△ADC的公共边,下列条件中不能判定△ABC≌△ADC的是( )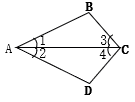 A、∠1=∠2,∠3=∠4 B、BC=DC,∠3=∠4 C、∠B=∠D,∠1=∠2 D、AB=AD,∠B=∠D8. 为锐角, , 点C在射线AM上,点B到射线AM的距离为d, , 若△ABC的形状、大小是唯一确定的,则x的取值范围是( )
A、∠1=∠2,∠3=∠4 B、BC=DC,∠3=∠4 C、∠B=∠D,∠1=∠2 D、AB=AD,∠B=∠D8. 为锐角, , 点C在射线AM上,点B到射线AM的距离为d, , 若△ABC的形状、大小是唯一确定的,则x的取值范围是( )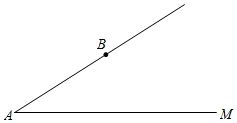 A、或 B、 C、 D、或9. 如图,在中, , , , 的垂直平分线交于点M,交于点E,的垂直平分线交于点N,交于点F,则的长为( )
A、或 B、 C、 D、或9. 如图,在中, , , , 的垂直平分线交于点M,交于点E,的垂直平分线交于点N,交于点F,则的长为( ) A、 B、 C、 D、10. 如图,在四边形中, , , 、分别是、上的点,将沿着翻折,得到 , 若ME//AD,EN//DC,则的度数为( )
A、 B、 C、 D、10. 如图,在四边形中, , , 、分别是、上的点,将沿着翻折,得到 , 若ME//AD,EN//DC,则的度数为( ) A、 B、 C、 D、11. 如图,在中, , , 是的平分线,设和的面积分别是 , , 则的值为( )
A、 B、 C、 D、11. 如图,在中, , , 是的平分线,设和的面积分别是 , , 则的值为( ) A、 B、 C、 D、12. 如图, , 垂足为点A, , , 射线 , 垂足为点B,一动点E从A点出发以沿射线运动,点D为射线上一动点,随着E点运动而运动,且始终保持 , 当点E经过( )秒时,与全等.(注:点E与A不重合)
A、 B、 C、 D、12. 如图, , 垂足为点A, , , 射线 , 垂足为点B,一动点E从A点出发以沿射线运动,点D为射线上一动点,随着E点运动而运动,且始终保持 , 当点E经过( )秒时,与全等.(注:点E与A不重合)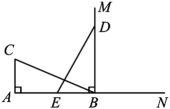 A、4 B、4、12 C、4、8、12 D、4、12、16
A、4 B、4、12 C、4、8、12 D、4、12、16二、填空题
-
13. 约分: .14. 已知等腰三角形的两边长分别为4和8,则它的周长等于 .15. 如图,D为内一点,平分 , , 垂足为D,交与点E, . 若 , , 则的长为 .
 16. 如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),点A的坐标为(-8,3),点B的坐标是 .
16. 如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),点A的坐标为(-8,3),点B的坐标是 . 17. 观察下面一列分式: , , , , , 根据规律,它的第项是 .
17. 观察下面一列分式: , , , , , 根据规律,它的第项是 .三、解答题
-
18. 计算:(1)、(2)、19. 化简求值: , 其中 .20. 如图,点B,E,C,F在同一直线上, , , . 线段与有什么数量关系?请说明理由.
 21. 如图,在平面直角坐标系中, .
21. 如图,在平面直角坐标系中, .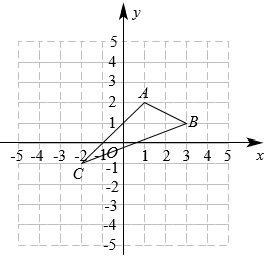
⑴在图中作出关于y轴的对称图形 , 并写出坐标;
⑵在x轴上画出点P,使最小.
22. 如图,计划在某小区建一个智能垃圾分类投放点P,需要满足以下条件:附近的两栋住宅楼A,B到智能垃圾分类投放点P的距离相等,P点到两条道路 , 的距离相等.请在图中利用尺规作图(保留作图痕迹,不写作法),确定点P的位置.


