山东省聊城市冠县2022-2023学年八年级上学期期中数学试题

试卷更新日期：2022-12-20 类型：期中考试

进入出卷网下载

一、单选题

1. 经过以下变化后所得到的三角形不能和 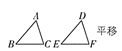$△ A B C$ 全等的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，点B，E，C，F在同一直线上，△ABC≌△DEF，BC=8，BF=13，则BE的长为（）

A、4 B、5 C、6.5 D、8

查看试题解析
3. 如图，一块三角形的玻璃打碎成四块，现要到玻璃店去配一块完全一样的玻璃，最简单的办法是（）

A、只带①去 B、带②③去 C、只带④去 D、带①③去

查看试题解析
4. 如图用直尺和圆规作已知角的平分线的示意图，由 $△ A D F ≌ △ A D E$ 可得 $∠ C A D = ∠ B A D$ ，由作图的过程可知，说明 $△ A D F ≌ △ A D E$ 的依据是（）

A、 $S S S$ B、 $S A S$ C、 $A S A$ D、 $A A S$

查看试题解析
5. 点P（-3，1）关于y轴对称点的坐标为（）

A、（1，-3） B、（3，1） C、（-3，-1） D、（3， -1）

查看试题解析
6. 下列手机中的图标是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
7. 某地兴建的幸福小区的三个出口A、B、C的位置如图所示，物业公司计划在不妨碍小区规划的建设下，想在小区内修建一个电动车充电桩，以方便业主，要求到三个出口的距离都相等，则充电桩应该在 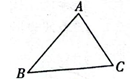$△ A B C$ （）

A、三条高线的交点处 B、三条中线的交点处 C、三个角的平分线的交点处 D、三条边的垂直平分线的交点处

查看试题解析
8. 若一个等腰三角形的两边长分别为5和12，则该三角形的周长是（）

A、5 B、5或12 C、22或29 D、29

查看试题解析
9. 若分式 $\frac{3}{x + 1}$ 有意义，则 $x$ 的取值范围（）

A、 $x \neq 1$ B、 $x \neq - 1$ C、 $x \neq 0$ D、 $x > 1$

查看试题解析
10. 如果把分式 $\frac{ab}{a + b}$ 中的a和b的值都变为原来的2倍，则分式的值（）

A、不变 B、是原来的 $\frac{1}{2}$ C、是原来的2倍 D、是原来的4倍

查看试题解析
11. 下列各式中，不能约分的分式是（）

A、 $\frac{2 a}{4 a^{2} b}$ B、 $\frac{a}{a^{2} - 3 a}$ C、 $\frac{a + b}{a^{2} + b^{2}}$ D、 $\frac{a^{2} - a b}{a^{2} - b^{2}}$

查看试题解析
12. 在等腰三角形ABC中， $C A = C B$ ，过点A作 $△ A B C$ 的高AD．若 $∠ A C D = 30 °$ ，则这个三角形的底角与顶角的度数比为（）

A、2：5或10：1 B、1：10 C、5：2 D、5：2或1：10

查看试题解析

二、填空题

13. 计算 $\frac{1}{x - 1} - \frac{1}{x (x - 1)}$ 的结果为．

查看试题解析
14. 如图所示的正方形的方格中，∠1＋∠3-∠2＝度．

查看试题解析
15. 如图，四边形ABCD是轴对称图形，直线AC是它的对称轴，若 $∠ B A C = 65 ° ， ∠ B = 50 °$ ，则 $∠ B C D$ 的大小为．

查看试题解析
16. 如图， $B O$ 平分 $∠ A B C$ ， $O D ⊥ B C$ 于点 $D$ ，点 $E$ 为射线 $B A$ 上一动点，若 $O D = 6$ ，则 $O E$ 的最小值为．

查看试题解析
17. 已知一张三角形纸片ABC（如图甲），其中 $A B = A C$ ，将纸片沿过点B的直线折叠，使点C落到AB边上的E点处，折痕为BD（如图乙），再将纸片沿过点E的直线折叠，点A恰好与点D重合，折痕为EF（如图丙）．原三角形纸片ABC中，∠ABC的大小为．

查看试题解析

三、解答题

18. 先化简，再求值： $(\frac{3}{x - 1} - x - 1) \div \frac{x^{2} - 4 x + 4}{x - 1}$ ，其中 $x = 3$ ．

查看试题解析
19. 两个城镇 $A$ 、 $B$ 与两条公路 $M E$ ， $M F$ 位置如图所示，其中 $M E$ 是东西方向的公路.现电信部门需在 $C$ 处修建一座信号发射塔，要求发射塔到两个城镇 $A$ 、 $B$ 的距离必须相等，到两条公路 $M E$ ， $M F$ 的距离也必须相等，且在 $∠ F M E$ 的内部，请在图中，用尺规作图找出符合条件的点 $C$ .（不写已知、求作、作法，只保留作图痕迹）

查看试题解析
20. 已知a、b、c分别是△ABC的三条边的边长，且a：b：c＝5：7：8，3a-2b+c=9，求△ABC的周长．

查看试题解析
21. 图，在 $Δ A B C$ 中， $B O$ 平分 $∠ A B C$ ， $C O$ 平分 $∠ A C B$ ，过点 $O$ 作 $B C$ 的平行线与 $A B$ ， $A C$ 分别相交于点 $M$ ， $N$ ．若 $A B = 5$ ， $A C = 6$ ，求 $Δ A M N$ 的周长．

查看试题解析
22. 如图，在△ABC中，AB=AC， $∠ B A C = 120 °$ ，点D、E在BC上，AD⊥AC，AE⊥AB．求证： $△ A E D$ 为等边三角形．

查看试题解析
23. 已知：如图，点D在线段AC上，点B在线段AE上，AE=AC，BE=DC，求证：∠E=∠C．

查看试题解析
24. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，把直角边 $B C$ 沿过点 $B$ 的某条直线折叠，使点 $C$ 落到边 $A B$ 上的一点 $D$ 处，当 $∠ A = 30 °$ 时，证明 $B D = D A$ ．

查看试题解析
25. 如图，在 $△ A B C$ 中， $A B$ 的垂直平分线分别交线段 $A B$ ， $B C$ 于点M，P， $A C$ 的垂直平分线分别交线段 $A C$ ， $B C$ 于点N，Q．

(1)、如图，当 $∠ B A C = 78 °$ 时，求 $∠ P A Q$ 的度数；

(2)、当 $∠ P A Q = 40 °$ 时，求 $∠ B A C$ 的度数．

查看试题解析