山西省临汾市2022-2023学年九年级上学期期中数学试卷
试卷更新日期:2022-12-20 类型:期中考试
一、单选题
-
1. 计算的结果为( )A、2 B、4 C、 D、2. 下列各组中的四条线段成比例的是( )A、4、2、1、3 B、1、2、3、5 C、3、4、5、6 D、1、2、2、43. 我们在解一元二次方程时,先将等号左边利用平方差公式进行因式分解,得到 , 再把它转化为两个一元一次方程或 , 进而解得 , , 这种解方程的过程体现出来的数学思想是( )A、抽象的思想 B、数形结合的思想 C、公理化的思想 D、转化的思想4. 若 , 则( )A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 图1是伸缩折叠不锈钢晾衣架的实物图,图2是它的侧面示意图,和相交于点O,点A,B之间的距离为1.2米, , 根据图2中的数据可得点C,D之间的距离为( )
 A、0.8米 B、0.86米 C、0.96米 D、1米7. 用配方法解方程 , 配方后所得的方程是( )A、 B、 C、 D、8. 如图,E是的边的延长线上的一点,连接 , 交边于点P.若 , 则与的周长之比为( )
A、0.8米 B、0.86米 C、0.96米 D、1米7. 用配方法解方程 , 配方后所得的方程是( )A、 B、 C、 D、8. 如图,E是的边的延长线上的一点,连接 , 交边于点P.若 , 则与的周长之比为( ) A、 B、 C、 D、9. 关于一元二次方程(k为常数)的根的情况,下列说法正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定根的情况10. 如图,在四边形中, , , E,F分别是 , 的中点,连接 , , , 点P为边上一点,过点P作 , 交于点Q,若 , 则的长为( )
A、 B、 C、 D、9. 关于一元二次方程(k为常数)的根的情况,下列说法正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定根的情况10. 如图,在四边形中, , , E,F分别是 , 的中点,连接 , , , 点P为边上一点,过点P作 , 交于点Q,若 , 则的长为( ) A、 B、1 C、 D、
A、 B、1 C、 D、二、填空题
-
11. 化为最简二次根式是 .12. 蝴蝶标本可以近似地看作轴对称图形.如图,将一只蝴蝶标本放在平面直角坐标系中,如果图中点A的坐标为(5,3),则其关于y轴对称的点B的坐标为 .
 13. 如图,在中,D是上一点, , , 垂足为E,F是的中点, , 则的长为 .
13. 如图,在中,D是上一点, , , 垂足为E,F是的中点, , 则的长为 . 14. 如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来( , , 与相交于点O),已知米,米,米,米,则汽车从A处前行的距离米时,才能发现C处的儿童.
14. 如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来( , , 与相交于点O),已知米,米,米,米,则汽车从A处前行的距离米时,才能发现C处的儿童.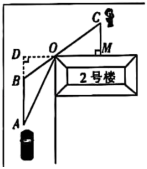 15. 如图,在中, , , 平分 , 若 , 则的长为 .
15. 如图,在中, , , 平分 , 若 , 则的长为 .
三、解答题
-
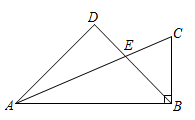
16.(1)、计算:;(2)、解方程: .17. 如图,在中, , E是边AC上一点,且 , 过点A作BE的垂线,交BE的延长线于点D,求证: .
 18. 某超市以每箱25元的进价购进一批水果,当该水果售价为40元/箱时,六月销售256箱,七、八月该水果十分畅销,销量持续上涨,在售价不变的基础上,八月的销量达到400箱.(1)、求七,八两月的月平均增长率;(2)、九月该超市为了减少库存,开始降价促销,经调查发现,该水果每箱降价1元,月销量在八月销量的基础上增加5箱,当该水果每箱降价多少元时,超市九月获利4250元?19. 如图,在平面直角坐标系内,三个顶点的坐标分别为 , , (网格中每个小正方形的边长为1),以点O为位似中心,画出的位似图形 , 相似比为2.
18. 某超市以每箱25元的进价购进一批水果,当该水果售价为40元/箱时,六月销售256箱,七、八月该水果十分畅销,销量持续上涨,在售价不变的基础上,八月的销量达到400箱.(1)、求七,八两月的月平均增长率;(2)、九月该超市为了减少库存,开始降价促销,经调查发现,该水果每箱降价1元,月销量在八月销量的基础上增加5箱,当该水果每箱降价多少元时,超市九月获利4250元?19. 如图,在平面直角坐标系内,三个顶点的坐标分别为 , , (网格中每个小正方形的边长为1),以点O为位似中心,画出的位似图形 , 相似比为2.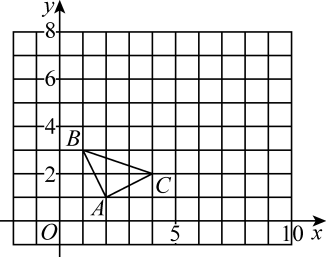 (1)、请在第一象限内画出;(2)、若以A,B,C,D为顶点的四边形是平行四边形,请直接写出满足条件的点D的坐标.20. 阅读与思考
(1)、请在第一象限内画出;(2)、若以A,B,C,D为顶点的四边形是平行四边形,请直接写出满足条件的点D的坐标.20. 阅读与思考阅读下列材料,并完成相应的任务:
法国数学家爱德华•卢卡斯以研究斐波那契数列而著名,他曾给出了求斐波那契数列第n项的表达式,创造出了检验素数的方法,还发明了汉诺塔问题.“卢卡斯数列”是以卢卡斯命名的一个整数数列,在股市中有广泛的应用.卢卡斯数列中的第n个数可以表示为 , 其中 . (说明:按照一定顺序排列着的一列数称为数列)
任务:
(1)、卢卡斯数列中的第1个数 , 第2个数;(2)、卢卡斯数列有一个重要特征:当时,满足 . 请根据这一规律写出卢卡斯数列中的第6个数 .21. 如图为幸福小区入口处安装的汽车出入道闸示意图.如图1,道闸关闭时,四边形是矩形.如图2,在道闸打开的过程中,边固定,直线l,连杆、分别绕点A、D转动,且边始终与边平行,P为上的一点(不与点C,D重合),过点P作直线l, , 垂足分别为E,F,即四边形是矩形,过点D作 , 垂足为Q,延长与相交于点R.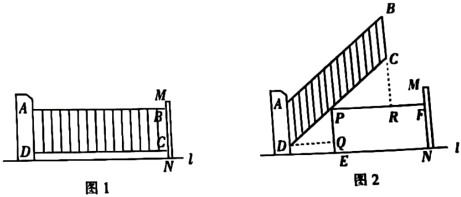 (1)、与相似吗?请判断并说明理由.(2)、若道闸长米,宽米,点D距地面米,米,米,米.
(1)、与相似吗?请判断并说明理由.(2)、若道闸长米,宽米,点D距地面米,米,米,米.①求点B到地面l的距离;
②求的长.
22. 综合与实践问题情境:如图,在中, , 将绕点B顺时针旋转得到 , 连接 , 连接并延长交于点F.
 (1)、 猜想验证:
(1)、 猜想验证:试猜想与是否相似?并证明你的猜想.
(2)、 探究证明:如图,连接交于点H,与相交于点G,是否成立?并说明理由.
(3)、 拓展延伸:若 , 直接写出的值.
23. 綜合与探究如图,在中, , 点M从点A开始沿边向点C以的速度运动,点N从点C开始沿边向点B以的速度运动,当点M到达点C时,点M,N同时停止运动.若 , 的长是的两根(其中 , 单位:).
 (1)、求 , 的长;(2)、如果点M,N分别从点A,C同时出发,那么几秒后,的面积为?(3)、如果点M,N分别从点A,C同时出发,是否能和相似?如果能,请求出运动的时间;如果不能,请说明理由.
(1)、求 , 的长;(2)、如果点M,N分别从点A,C同时出发,那么几秒后,的面积为?(3)、如果点M,N分别从点A,C同时出发,是否能和相似?如果能,请求出运动的时间;如果不能,请说明理由.