山东省淄博市临淄区2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-12-20 类型:期中考试
一、单选题
-
1. 已知函数y=(m-2)是反比例函数,则m的值为( )A、2 B、-2 C、2或-2 D、任意实数2. 如图,在坡角为30°的斜坡上要栽两棵树,要求它们之间的水平距离AC为6m,则这两棵树之间的坡面AB的长为( )
 A、12m B、3m C、4m D、12m3. 将抛物线 向左平移3个单位长度,再向下平移2个单位长度,得到抛物线的解析式是( )A、 B、 C、 D、4. 对于二次函数y=(x+1)2+2的图象,下列说法正确的是( )A、开口向下 B、对称轴是直线x=-1 C、顶点坐标是(1,2) D、与x轴有两个交点5. 在同一平面直角坐标系中,一次函数与二次函数的图象大致为( )A、
A、12m B、3m C、4m D、12m3. 将抛物线 向左平移3个单位长度,再向下平移2个单位长度,得到抛物线的解析式是( )A、 B、 C、 D、4. 对于二次函数y=(x+1)2+2的图象,下列说法正确的是( )A、开口向下 B、对称轴是直线x=-1 C、顶点坐标是(1,2) D、与x轴有两个交点5. 在同一平面直角坐标系中,一次函数与二次函数的图象大致为( )A、 B、
B、 C、
C、 D、
D、 6. 已知 ,用计算器求∠A的大小,下列按键顺序正确的是( )
6. 已知 ,用计算器求∠A的大小,下列按键顺序正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 如图,在平面直角坐标系中,函数与的图象交于点 , 则代数式的值为( )
7. 如图,在平面直角坐标系中,函数与的图象交于点 , 则代数式的值为( ) A、 B、 C、 D、8. 如图,A,B是双曲线 上的两个点,过点A作AC⊥x轴,交OB于点D,垂足为C,若△ODC的面积为1,D为OB的中点,则k的值为( )
A、 B、 C、 D、8. 如图,A,B是双曲线 上的两个点,过点A作AC⊥x轴,交OB于点D,垂足为C,若△ODC的面积为1,D为OB的中点,则k的值为( )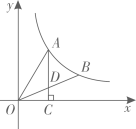 A、 B、2 C、4 D、89. 对称轴为直线 的抛物线 、b、c为常数,且 如图所示,小明同学得出了以下结论: , , , , 为任意实数), 当 时,y随x的增大而增大.其中结论正确的个数为( )
A、 B、2 C、4 D、89. 对称轴为直线 的抛物线 、b、c为常数,且 如图所示,小明同学得出了以下结论: , , , , 为任意实数), 当 时,y随x的增大而增大.其中结论正确的个数为( )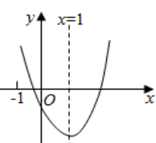 A、3 B、4 C、5 D、610. 如图,在平面直角坐标系中, , , , …的斜边都在坐标轴上, . 若点的坐标为 , , , …,则依此规律,点的纵坐标为( )
A、3 B、4 C、5 D、610. 如图,在平面直角坐标系中, , , , …的斜边都在坐标轴上, . 若点的坐标为 , , , …,则依此规律,点的纵坐标为( ) A、 B、 C、0 D、
A、 B、 C、0 D、二、填空题
-
11. 二次函数的图象经过原点,则k的值为 .12. 已知方程有两个不相等的实数根 , . 而点 , 为反比例函数的图象上两点,若 , 则(填“>”或“<”或“=”).13. 已知二次函数的部分图象如图所示,则关于x的一元二次不等式的解集为 .
 14. △ABC中,∠ABC=30°,AB=4 ,AC=4,则BC= .15. 如图,在平面直角坐标系中,O为坐标原点,点B在x轴的正半轴上,四边形OBCA是平行四边形, , 反比例函数在第一象限内的图像经过点A,与BC交于点F,若点F为BC的中点,且的面积为12,则m的值为 .
14. △ABC中,∠ABC=30°,AB=4 ,AC=4,则BC= .15. 如图,在平面直角坐标系中,O为坐标原点,点B在x轴的正半轴上,四边形OBCA是平行四边形, , 反比例函数在第一象限内的图像经过点A,与BC交于点F,若点F为BC的中点,且的面积为12,则m的值为 .
三、解答题
-
16. 计算(1)、;(2)、;(3)、已知三角函数有如下的公式: , 利用该公式求的值.17. 如图,直线y=﹣x+1与反比例函数y= 的图象相交于点A、B,过点A作AC⊥x轴,垂足为点C(﹣2,0),连接AC、BC.
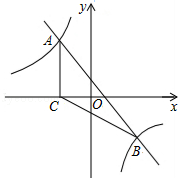 (1)、求反比例函数的解析式;(2)、求S△ABC;(3)、利用函数图象直接写出关于x的不等式﹣x+1< 的解集.18. 已知:如图在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12, . 求:
(1)、求反比例函数的解析式;(2)、求S△ABC;(3)、利用函数图象直接写出关于x的不等式﹣x+1< 的解集.18. 已知:如图在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12, . 求: (1)、线段DC的长;(2)、tan∠EDC的值.19. 王叔叔计划购买一套商品房,首付30万元后,剩余部分用贷款并按“等额本金”的形式偿还,即贷款金额按月分期还款,每月所还贷款本金数相同.设王叔叔每月偿还贷款本金y万元,x个月还清,且y是x的反比例函数,其图象如图所示.
(1)、线段DC的长;(2)、tan∠EDC的值.19. 王叔叔计划购买一套商品房,首付30万元后,剩余部分用贷款并按“等额本金”的形式偿还,即贷款金额按月分期还款,每月所还贷款本金数相同.设王叔叔每月偿还贷款本金y万元,x个月还清,且y是x的反比例函数,其图象如图所示. (1)、求y与x的函数关系式;(2)、求王叔叔购买的商品房的总价;(3)、若王叔叔计划每月偿还贷款本金不超过2000元,则至少需要多少个月还清?20. 已知函数 .(1)、求证:无论m为任何实数,此二次函数的图象与x轴都有两个不同的交点;(2)、若函数图象不经过第三象限,求m的范围;(3)、求证:无论m为何实数,此二次函数的图象一定经过第四象限.21. 如图,小文在数学综合实践活动中,利用所学的数学知识测量居民楼的高度 , 在居民楼前方有一斜坡,坡长 , 斜坡的倾斜角为 , . 小文在C点处测得楼顶端A的仰角为 , 在D点处测得楼顶端A的仰角为(点A,B,C,D在同一平面内).
(1)、求y与x的函数关系式;(2)、求王叔叔购买的商品房的总价;(3)、若王叔叔计划每月偿还贷款本金不超过2000元,则至少需要多少个月还清?20. 已知函数 .(1)、求证:无论m为任何实数,此二次函数的图象与x轴都有两个不同的交点;(2)、若函数图象不经过第三象限,求m的范围;(3)、求证:无论m为何实数,此二次函数的图象一定经过第四象限.21. 如图,小文在数学综合实践活动中,利用所学的数学知识测量居民楼的高度 , 在居民楼前方有一斜坡,坡长 , 斜坡的倾斜角为 , . 小文在C点处测得楼顶端A的仰角为 , 在D点处测得楼顶端A的仰角为(点A,B,C,D在同一平面内).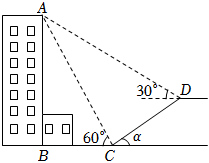 (1)、求C,D两点的高度差;(2)、求居民楼的高度 . (结果精确到 , 参考数据:)22. 我国互联网发展日新月异,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条60元,当售价为每条100元时,每月可销售120条.为了吸引更多顾客,该网店采取降价措施.据市场调查知:销售单价每降1元,则每月可多销售6条.设每条裤子的售价为x元(x为正整数),每月的销售量为y条.(1)、直接写出y与x的函数关系式:(2)、设该网店每月获得的利润为w元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定每月从利润中捐出300元资助贫困学生.为了保证捐款后每月利润不低于4950元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?23. 如图,抛物线与直线交于点 , . 点D是抛物线上A,B两点间的一个动点(不与点A,B重合),直线与y轴平行,交直线于点C,连接 .
(1)、求C,D两点的高度差;(2)、求居民楼的高度 . (结果精确到 , 参考数据:)22. 我国互联网发展日新月异,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条60元,当售价为每条100元时,每月可销售120条.为了吸引更多顾客,该网店采取降价措施.据市场调查知:销售单价每降1元,则每月可多销售6条.设每条裤子的售价为x元(x为正整数),每月的销售量为y条.(1)、直接写出y与x的函数关系式:(2)、设该网店每月获得的利润为w元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定每月从利润中捐出300元资助贫困学生.为了保证捐款后每月利润不低于4950元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?23. 如图,抛物线与直线交于点 , . 点D是抛物线上A,B两点间的一个动点(不与点A,B重合),直线与y轴平行,交直线于点C,连接 . (1)、求抛物线的解析式;(2)、设点D的横坐标为m,的面积为S,求S关于m的函数关系式,并求出当S取最大值时的点C的坐标;(3)、点D为抛物线的顶点,点P是抛物线上的动点,点Q是直线上的动点.当以点P,Q,C,D为顶点的四边形是平行四边形时,求出点Q的坐标.
(1)、求抛物线的解析式;(2)、设点D的横坐标为m,的面积为S,求S关于m的函数关系式,并求出当S取最大值时的点C的坐标;(3)、点D为抛物线的顶点,点P是抛物线上的动点,点Q是直线上的动点.当以点P,Q,C,D为顶点的四边形是平行四边形时,求出点Q的坐标.