山东省威海市文登区2022-2023学年九年级上学期期中数学试题

试卷更新日期：2022-12-20 类型：期中考试

进入出卷网下载

一、单选题

1. $s i n 45 °$ 的倒数是（）

A、 $2 \sqrt{2}$ B、 $\sqrt{2}$ C、 $\frac{\sqrt{2}}{2}$ D、1

查看试题解析
2. 在Rt△ACB中，∠C＝90°，AB＝8，sinA＝ $\frac{3}{4}$ ，则BC的长为（）

A、6 B、7.5 C、8 D、12.5

查看试题解析
3. 对于反比例函数 $y = - \frac{2022}{x}$ 的图象，下列说法不一定正确的是（）

A、图象经过点(1，-2022) B、图象分布在二、四象限 C、图象关于原点成中心对称 D、图象上的两点 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ ，若 $x_{1} > x_{2}$ ，则 $y_{1} > y_{2}$

查看试题解析
4. 已知一个不等臂跷跷板 $A B$ 长4米，支撑柱 $O H$ 垂直地面，如图1，当 $A B$ 的一端A着地时， $A B$ 与地面夹角的正弦值为 $\frac{1}{2}$ ﹔如图2，当 $A B$ 的另一端B着地时， $A B$ 与地面夹角的正弦值为 $\frac{1}{3}$ ，则支撑柱 $O H$ 的长为（）

A、0.5米 B、0.6米 C、 $\frac{1}{2} \sqrt{3}$ 米 D、0.8米

查看试题解析
5. 如图，在4×4正方形网格中，点A、B、C为网格交点，AD⊥BC，垂足为D，则sin∠BAD的值为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{4}$ C、 $\frac{4}{5}$ D、 $\frac{3}{5}$

查看试题解析
6. 已知：二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，下列结论中：① $a b c > 0$ ；② $2 a + b < 0$ ；③ $a + b > m (a m + b)$ （ $m \neq 1$ 的实数）；④ $(a + c)^{2} < b^{2}$ ；⑤ $a > 1$ ，其中正确的是（）

A、2个 B、3个 C、4个 D、1个

查看试题解析
7. 如图，圆规两脚 $O A ， O B$ 张开的角度 $∠ A O B$ 为α， $O A = O B = 10$ ，则两脚张开的距离 $A B$ 为（　　）

A、 $10 s i n α$ B、 $10 c o s α$ C、 $20 s i n \frac{a}{2}$ D、 $20 c o s \frac{a}{2}$

查看试题解析
8. 已知二次函数y＝ax²＋bx＋c的x与y的部分对应值如下表：
x
…
－3
－2
－1
0
1
3
…
y
…
－27
－13
－3
3
5
－3
…
下列结论：①a＜0；②方程ax²＋bx＋c＝3的解为x₁＝0， x₂＝2；③当x＞2时，y＜0．
其中所有正确结论的序号是（）

A、①②③ B、① C、②③ D、①②

查看试题解析
9. 有一个矩形苗圃园，其中一边靠墙，另外三边用长为 $20 m$ 的篱笆围成．已知墙长为 $15 m ，$ 若平行于墙的一边长不小于 $8 m ，$ 则这个苗圃园面积的最大值和最小值分别为（）

A、 $48 m^{2} ， 37.5 m^{2}$ B、 $50 m^{2} ， 32 m^{2}$ C、 $50 m^{2} ， 37.5 m^{2}$ D、 $48 m^{2} ， 32 m^{2}$

查看试题解析
10. 如图，直线 $y = - \frac{4}{3} x + 4$ 与x轴、y轴分别相交于点A，B，过点B作 $B C ⊥ A B$ ，使 $B C = 2 B A$ ．将 $△ A B C$ 绕点O顺时针旋转，每次旋转90°，当第2022次旋转结束时，点C的对应点 $C^{'}$ 落在反比例函数 $y = \frac{k}{x}$ 的图象上，则k的值为（）

A、-40 B、40 C、80 D、-80

查看试题解析

二、填空题

11. 函数y＝ $\frac{x}{\sqrt{x + 3}} + \frac{1}{x - 1}$ 的自变量x的取值范围是

查看试题解析
12. 若抛物线 $y = a x^{2} - x + 1$ 与x轴有公共点，则a的取值范围是

查看试题解析
13. 已知二次函数 $y = - {(x - m)}^{2} - 1$ ，当 $x > 1$ 时，y随x的增大而减小，则m的取值范围

查看试题解析
14. 如图，一架水平飞行的无人机在A处测得正前方河岸边C处的俯角为α， $t a n α = 2$ ，无人机沿水平线AF方向继续飞行80米至B处时，被河对岸D处的小明测得其仰角为 $30 °$ ．无人机距地面的垂直高度用AM表示，点M，C，D在同一条直线上，其中 $M C = 100$ 米，则河流的宽度CD为．

查看试题解析
15. 把二次函数 $y = 2 (x - 2)^{2} - 5$ 的图象向右平移2个单位后，再向上平移3个单位，所得的函数图象顶点坐标

查看试题解析
16. 如图，在反比例函数 $y = \frac{2}{x} (x > 0)$ 的图象上，有点 $P_{1}$ ， $P_{2}$ ， $P_{3}$ ， $P_{4}$ ， $\dots$ ， $P_{n}$ ， $\dots$ ，它们的横坐标依次为1，2，3，4， $\dots$ ， n， $\dots$ ，分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为 $S_{1}$ ， $S_{2}$ ， $S_{3}$ ， $S_{5}$ ， $\dots$ ， $S_{n}$ ， $\dots$ ，则 $S_{1} + S_{2} + S_{3} + \dots + S_{2022}$ 的结果为

查看试题解析

三、解答题

17. 计算 $2 c o s 30 ° - t a n 45 ° - \sqrt{{(1 - t a n 60 °)}^{2}}$

查看试题解析
18. 小丽与爸妈在公园里荡秋千．如图，小丽坐在秋千的起始位置A处，OA与地面垂直，两脚在地面上用力一蹬，妈妈在距地面1.2 m高的B处接住她后用力一推，爸爸在C处接住她．若妈妈与爸爸到OA的水平距离BD、CE分别为1.8 m和2.4 m，∠BOC＝90°．

(1)、△CEO与△ODB全等吗？请说明理由．

(2)、爸爸在距离地面多高的地方接住小丽的？

(3)、秋千的起始位置A处与距地面的高是m．

查看试题解析
19. 如图1所示，某公园有一个直径为16米的圆形喷水池，喷出的水柱为抛物线，且各方向喷出的水柱恰好落在水池内，过喷水管口所在铅垂线 $O A$ 每一个截面均可得到两条关于 $O A$ 对称的抛物线，如图2，以喷水池中心O为原点，喷水管口所在铅垂线为纵轴，建立平面直角坐标系．

(1)、若喷出的水柱在距水池中心3米处达到最高，且高度为5米，求水柱所在抛物线的函数表达式；

(2)、王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？

查看试题解析
20. 资阳市为实现5G网络全覆盖，2020－2025年拟建设5G基站七千个.如图，在坡度为 $i = 1 ： 2.4$ 的斜坡 $C B$ 上有一建成的基站塔 $A B$ ，小芮在坡脚C测得塔顶A的仰角为 $45 °$ ，然后她沿坡面 $C B$ 行走13米到达D处，在D处测得塔顶A的仰角为 $53 °$ （点A、B、C、D均在同一平面内）（参考数据： $s i n 53 ° \approx \frac{4}{5} ， c o s 53 ° \approx \frac{3}{5} ， t a n 53 ° \approx \frac{4}{3}$ ）

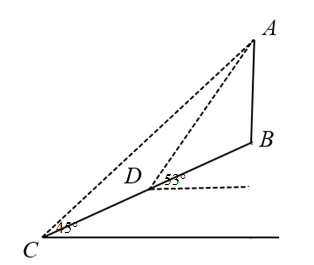(1)、求D处的竖直高度；

(2)、求基站塔 $A B$ 的高.

查看试题解析
21. 小丽家饮水机中原有水的温度为20℃，通电开机后，饮水机自动开始加热，此过程中水温y（℃）与开机时间x（分）满足一次函数关系，当加热到100℃时自动停止加热，随后水温开始下降，此过程中水温y（℃）与开机时间x（分）成反比例关系，当水温降至20℃时，饮水机又自动开始加热……，重复上述程序（如图所示），根据图中提供的信息，解答问题：

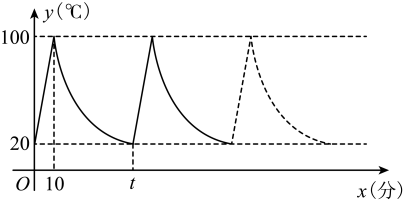(1)、当 $0 \leq x \leq 10$ 时，求水温y（℃）与开机时间x（分）的函数关系式；

(2)、求图中t的值；

(3)、若小丽在通电开机后即外出散步，请你预测小丽散步70分钟回到家时，饮水机内的温度约为多少℃？

查看试题解析
22. 浙江省温州市是全国旅游胜地，2020年受新冠疫情的影响，来温的外来游客在逐年下降. 某景区外来游客人数从2019年的2.25万下降到2021年的1.44万．

(1)、求2019年到2021年该景区外来游客人数平均每年降低的百分率；

(2)、该景区要建一个游乐场（如图所示），其中 $A D$ 、 $C D$ 分别靠现有墙 $D M$ 、 $D N$ （墙 $D M$ 长为27米，墙 $D N$ 足够长），其余用篱笆围成.篱笆 $D E$ 将游乐场隔成等腰直角 $△ C E D$ 和长方形 $A D E B$ 两部分，并在三处各留2米宽的大门．已知篱笆总长为54米．

①当 $A B$ 多长时，游乐场的面积为320平方米？

②当 $A B =$ _▲_米时，游乐场的面积达到最大，最大为_▲_平方米．

查看试题解析
23. 矩形OABC的顶点A，C分别在x，y轴的正半轴上，点F是边BC上的一个动点(不与点B，C重合)，过点F的反比例函数 $y = \frac{k}{x} (x ＞ 0)$ 的图象与边AB交于点E(8，m)，AB＝4．

(1)、如图1，若BE＝3AE．
①求反比例函数的表达式；
②将矩形OABC折叠，使O点与F点重合，折痕分别与x，y轴交于点H，G，求线段OG的长度．

(2)、如图2，连接OF，EF，请用含m的关系式表示OAEF的面积，并求OAEF的面积的最大值．

查看试题解析
24. 如图，在平面直角坐标系中，抛物线y＝ $\frac{1}{2}$ x²＋bx＋c经过点A（-4，0），点M为抛物线的顶点，点B在y轴上，且OA＝OB，直线AB与抛物线在第一象限交于点C（2，6）．

(1)、求抛物线的解析式及顶点M的坐标；

(2)、求直线AB的函数解析式及sin∠ABO的值；连接OC．若过点O的直线交线段AC于点P，将三角形AOC的面积分成1：2的两部分，请求出点P的坐标；

(3)、在坐标平面内是否存在点N，使以点A、O、C、N为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．

查看试题解析

x	…	－3	－2	－1	0	1	3	…
y	…	－27	－13	－3	3	5	－3	…