山东省烟台市芝罘区2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-12-20 类型:期中考试
一、单选题
-
1. 在中, , 则下列式子定成立的是A、 B、 C、 D、2. 二次函数 图象的顶点坐标是( )A、 B、 C、 D、3. 在中, , , , 则的长为( )A、5 B、 C、45 D、4. 抛物线可由抛物线平移得到,平移方法是( )A、先向右平移3个单位,再向下平移4个单位 B、先向左平移6个单位,再向上平移5个单位 C、先向左平移3个单位,再向下平移4个单位 D、先回右平移3个单位,再向上平移1个单位5. 已知 ,用计算器求∠A的大小,下列按键顺序正确的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 6. 厂房屋顶人字形(等腰三角形)钢架的中柱(D为底边中点)长10米, , 则跨度的长是( )
6. 厂房屋顶人字形(等腰三角形)钢架的中柱(D为底边中点)长10米, , 则跨度的长是( ) A、米 B、米 C、米 D、米7. 设是抛物线上的三点,则 , , 的大小关系用“<”连接正确的是( )A、 B、 C、 D、8. 已知直线 , 且相邻的两条平行直线间的距离均等,将一个含45°的直角三角板按图示放置,使其三个顶点分别在三条平行线上,则的值是( )
A、米 B、米 C、米 D、米7. 设是抛物线上的三点,则 , , 的大小关系用“<”连接正确的是( )A、 B、 C、 D、8. 已知直线 , 且相邻的两条平行直线间的距离均等,将一个含45°的直角三角板按图示放置,使其三个顶点分别在三条平行线上,则的值是( ) A、 B、 C、 D、9. 在同一坐标系内,一次函数与二次函数的图像可能是( )A、
A、 B、 C、 D、9. 在同一坐标系内,一次函数与二次函数的图像可能是( )A、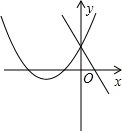 B、
B、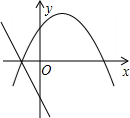 C、
C、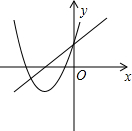 D、
D、 10. 如图,已知的三个顶点均在正方形格点上,则的值为( )
10. 如图,已知的三个顶点均在正方形格点上,则的值为( ) A、 B、 C、 D、11. 如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数解析式是 , 则该运动员此次掷铅球的成绩是( )
A、 B、 C、 D、11. 如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数解析式是 , 则该运动员此次掷铅球的成绩是( )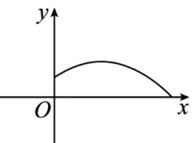 A、6m B、12m C、8m D、10m12. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,其对称轴为直线x=﹣ , 且与x轴的一个交点坐标为(﹣2,0).下列结论:①abc>0;②a=b;③2a+c=0;④关于x的一元二次方程ax2+bx+c﹣1=0有两个相等的实数根.其中正确结论的序号是( )
A、6m B、12m C、8m D、10m12. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,其对称轴为直线x=﹣ , 且与x轴的一个交点坐标为(﹣2,0).下列结论:①abc>0;②a=b;③2a+c=0;④关于x的一元二次方程ax2+bx+c﹣1=0有两个相等的实数根.其中正确结论的序号是( )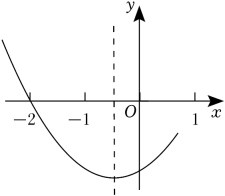 A、①③ B、②④ C、③④ D、②③
A、①③ B、②④ C、③④ D、②③二、填空题
-
13. 函数y= 的自变量x的取值范围是 .14. 如图,在中, , 点在上, , , 则的值是 .
 15. 在平面直角坐标系中,若函数的图像与坐标轴只有一个交点,那么的取值范围是 .16. 下图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯次点B到点C上升的高度h是m.
15. 在平面直角坐标系中,若函数的图像与坐标轴只有一个交点,那么的取值范围是 .16. 下图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯次点B到点C上升的高度h是m. 17. 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值= .
17. 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值= . 18. 已知函数的图像过点和 , 且 , 则的取值范围是 .
18. 已知函数的图像过点和 , 且 , 则的取值范围是 .三、解答题
-
19. 计算: .20. 已知抛物线 .
 (1)、求出这个抛物线的对称轴方程和顶点坐标;(2)、在给定的坐标系中画出这条抛物线,设抛物线与x轴交于A,B两点,y轴交于点C,求的面积.21. 如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们西北方向距离6海里的B处有一艘捕鱼船正在沿南偏西75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以14海里的速度沿北偏西某一方向航行,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
(1)、求出这个抛物线的对称轴方程和顶点坐标;(2)、在给定的坐标系中画出这条抛物线,设抛物线与x轴交于A,B两点,y轴交于点C,求的面积.21. 如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们西北方向距离6海里的B处有一艘捕鱼船正在沿南偏西75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以14海里的速度沿北偏西某一方向航行,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间. 22. 如图,一个高3米的涵洞的剖面示意图为一段抛物线,涵洞底部宽米,涵洞内水面宽度米.
22. 如图,一个高3米的涵洞的剖面示意图为一段抛物线,涵洞底部宽米,涵洞内水面宽度米. (1)、请建立适当的平而直角坐标系,并求出抛物线的函数关系式;(2)、求涵洞内的水深.23. 如图,某超市计划将门前的部分楼梯改造成无障碍通道.已知楼梯共有五级均匀分布的台阶,高AB=0.75m,斜坡AC的坡比为1:2,将要铺设的通道前方有一井盖,井盖边缘离楼梯底部的最短距离ED=2.55m.为防止通道遮盖井盖,所铺设通道的坡角不得小于多少度?(结果精确到1)
(1)、请建立适当的平而直角坐标系,并求出抛物线的函数关系式;(2)、求涵洞内的水深.23. 如图,某超市计划将门前的部分楼梯改造成无障碍通道.已知楼梯共有五级均匀分布的台阶,高AB=0.75m,斜坡AC的坡比为1:2,将要铺设的通道前方有一井盖,井盖边缘离楼梯底部的最短距离ED=2.55m.为防止通道遮盖井盖,所铺设通道的坡角不得小于多少度?(结果精确到1)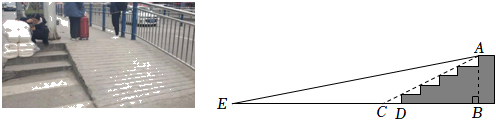
(参考数据表)
计算器按键顺序
计算结果(已精确到0.001)

11.310

0.003
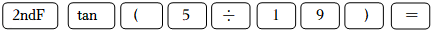
14.744

0.005
24. 为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)、试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)、当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)、为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
25. 如图①,已知直线与x轴交于点A,与y轴交于点C,抛物线经过A,C两点,且与x轴的另一个交点为B,对称轴为直线 , D是第二象限内抛物线上的动点,设点D的横坐标为m. (1)、求抛物线的表达式;(2)、求四边形面积S的最大值及此时D点的坐标;(3)、过点D向y轴作垂线(如图②),垂足为点E,是否存在点D,使与相似?若存在,请求出点D横坐标m的值;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、求四边形面积S的最大值及此时D点的坐标;(3)、过点D向y轴作垂线(如图②),垂足为点E,是否存在点D,使与相似?若存在,请求出点D横坐标m的值;若不存在,请说明理由.