山东省烟台市栖霞市2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-12-20 类型:期中考试
一、单选题
-
1. 若点(﹣5,y1),(﹣3,y2),(3,y3)都在反比例函数的图象上,则( )A、y1>y2>y3 B、y2>y1>y3 C、y3>y1>y2 D、y1>y3>y22. 一次函数和反比例函数在同一平面直角坐标系中的图象如图所示,则二次函数的图象可能是( )
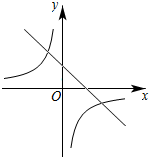 A、
A、 B、
B、 C、
C、 D、
D、 3. 正比例函数 与反比例函数 的图象相交于A,C两点,AB⊥x轴于点B,CD⊥x轴于点D(如图),则四边形ABCD的面积为( )
3. 正比例函数 与反比例函数 的图象相交于A,C两点,AB⊥x轴于点B,CD⊥x轴于点D(如图),则四边形ABCD的面积为( ) A、1 B、 C、2 D、4. 如图,的顶点是正方形网格的格点,则的值为( )
A、1 B、 C、2 D、4. 如图,的顶点是正方形网格的格点,则的值为( )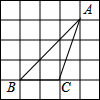 A、 B、 C、 D、5. 如图,是电杆的一根拉线,测得米, , 则拉线的长为( )
A、 B、 C、 D、5. 如图,是电杆的一根拉线,测得米, , 则拉线的长为( )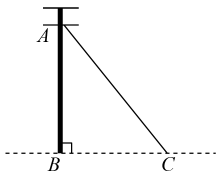 A、米 B、米 C、米 D、米6. 将二次函数配方为的形式为( )A、 B、 C、 D、7. 如图,甲、乙为两座建筑物,它们之间的水平距离为 , 在A点测得D点的仰角为 , 在B点测得D点的仰角为 , 则乙建筑物的高度为( )
A、米 B、米 C、米 D、米6. 将二次函数配方为的形式为( )A、 B、 C、 D、7. 如图,甲、乙为两座建筑物,它们之间的水平距离为 , 在A点测得D点的仰角为 , 在B点测得D点的仰角为 , 则乙建筑物的高度为( )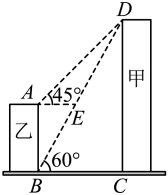 A、 B、 C、 D、8. 若A( , ),B( , ),C( , )为二次函数的图象上的三点,则的大小关系是( )A、 B、 C、 D、9. 将抛物线向右平移2个单位,再向上平移1个单位,所得抛物线相应的函数表达式是( )A、 B、 C、 D、10. 若函数y=ax2﹣x+1(a为常数)的图象与x轴只有一个交点,那么a满足( )A、a= B、a≤ C、a=0或a=﹣ D、a=0或a=
A、 B、 C、 D、8. 若A( , ),B( , ),C( , )为二次函数的图象上的三点,则的大小关系是( )A、 B、 C、 D、9. 将抛物线向右平移2个单位,再向上平移1个单位,所得抛物线相应的函数表达式是( )A、 B、 C、 D、10. 若函数y=ax2﹣x+1(a为常数)的图象与x轴只有一个交点,那么a满足( )A、a= B、a≤ C、a=0或a=﹣ D、a=0或a=二、填空题
-
11. 已知函数求x的取值范围 .12. 如图,河堤横断面迎水坡的坡比是 , 堤高 , 则坡面的长度是m.
 13. 轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则B处与灯塔A的距离是海里.
13. 轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则B处与灯塔A的距离是海里.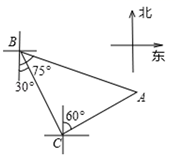 14. 如图,以地面为x轴,一名男生推铅球,铅球行进高度y(单位:米)与水平距离x(单位:米)之间的关系是 . 则他将铅球推出的距离是米.
14. 如图,以地面为x轴,一名男生推铅球,铅球行进高度y(单位:米)与水平距离x(单位:米)之间的关系是 . 则他将铅球推出的距离是米.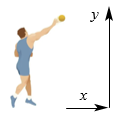 15. 某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为元(利润=总销售额-总成本).
15. 某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为元(利润=总销售额-总成本).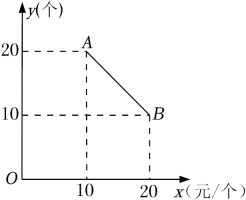 16. 二次函数的大致图象如图所示,顶点坐标为 , 下列结论:①;②;③若方程有两个根和 , 且 , 则;④的最小值为 . 其中正确结论的是 .
16. 二次函数的大致图象如图所示,顶点坐标为 , 下列结论:①;②;③若方程有两个根和 , 且 , 则;④的最小值为 . 其中正确结论的是 .
三、解答题
-
17. 计算(1)、(2)、 .18. 如图,在△ABC中,∠C=90°,点D,E分别在AC,AB上,BD平分∠ABC,DE⊥AB于点E,AE=6,cosA= .
 (1)、求CD的长;(2)、求tan∠DBC的值.19. 已知二次函数的部分图象如图所示.
(1)、求CD的长;(2)、求tan∠DBC的值.19. 已知二次函数的部分图象如图所示. (1)、求该函数图象与x轴的另一个交点坐标;(2)、求这个二次函数的解析式;(3)、直接写出满足时x的取值范围.(4)、求不等式的解.20. 如图,一次函数()与反比例函数()的图象交于A , B两点.
(1)、求该函数图象与x轴的另一个交点坐标;(2)、求这个二次函数的解析式;(3)、直接写出满足时x的取值范围.(4)、求不等式的解.20. 如图,一次函数()与反比例函数()的图象交于A , B两点.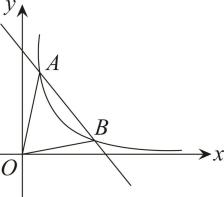 (1)、求一次函数的解析式;(2)、根据图象,直接写出使成立的的取值范围;(3)、求的面积.21. 为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:
(1)、求一次函数的解析式;(2)、根据图象,直接写出使成立的的取值范围;(3)、求的面积.21. 为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题: (1)、药物燃烧时,y关于x的函数关系式为 , 自变量x的取值范围为;药物燃烧后,y关于x的函数关系式为 .(2)、研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过 分钟后,员工才能回到办公室;(3)、研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?22. 某型号飞机的机翼形状如图所示,根据图中数据计算AC,BD和AB的长度(结果保留小数点后两位).
(1)、药物燃烧时,y关于x的函数关系式为 , 自变量x的取值范围为;药物燃烧后,y关于x的函数关系式为 .(2)、研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过 分钟后,员工才能回到办公室;(3)、研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?22. 某型号飞机的机翼形状如图所示,根据图中数据计算AC,BD和AB的长度(结果保留小数点后两位).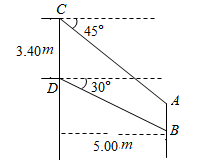 23. 现要修建一条隧道,其截面为抛物线型,如图所示,线段表示水平的路面,以O为坐标原点,以所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.根据设计要求: , 该抛物线的顶点P到的距离为.
23. 现要修建一条隧道,其截面为抛物线型,如图所示,线段表示水平的路面,以O为坐标原点,以所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.根据设计要求: , 该抛物线的顶点P到的距离为. (1)、求满足设计要求的抛物线的函数表达式;(2)、现需在这一隧道内壁上安装照明灯,如图所示,即在该抛物线上的点A、B处分别安装照明灯.已知点A、B到的距离均为 , 求点A、B的坐标.24. 某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中8≤x≤15,且x为整数).当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天的销售量为95件.(1)、求y与x之间的函数关系式.(2)、若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为多少元?(3)、设该商店销售这种消毒用品每天获利w(元),当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?25. 如图,在平面直角坐标系中,抛物线(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,-4),点C坐标为(2,0).
(1)、求满足设计要求的抛物线的函数表达式;(2)、现需在这一隧道内壁上安装照明灯,如图所示,即在该抛物线上的点A、B处分别安装照明灯.已知点A、B到的距离均为 , 求点A、B的坐标.24. 某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中8≤x≤15,且x为整数).当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天的销售量为95件.(1)、求y与x之间的函数关系式.(2)、若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为多少元?(3)、设该商店销售这种消毒用品每天获利w(元),当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?25. 如图,在平面直角坐标系中,抛物线(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,-4),点C坐标为(2,0).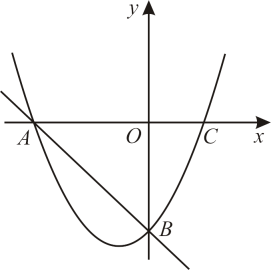 (1)、求此抛物线的函数解析式.(2)、点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.(3)、点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.
(1)、求此抛物线的函数解析式.(2)、点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.(3)、点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.