山东省烟台市蓬莱区2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-12-20 类型:期中考试
一、单选题
-
1. 在 中, , ,则 等于( )A、 B、 C、 D、2. 把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦函数值( )
A、不变 B、缩小为原来的 C、扩大为原来的3倍 D、不能确定3. 若点( , ),( , ),( , ),都是反比例函数图像上的点,并且 , 则下列各式中正确的是( )A、 B、 C、 D、4. 在平面直角坐标系中,抛物线与坐标轴交点的个数是( ).A、3 B、2 C、1 D、05. 若用我们数学课本上采用的科学计算器计算sin36 18',按键顺序正确的是( )A、 B、
B、 C、
C、 D、
D、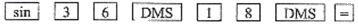 6. 将抛物线 向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线解析式为( )A、 B、 C、 D、7. 如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )
6. 将抛物线 向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线解析式为( )A、 B、 C、 D、7. 如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )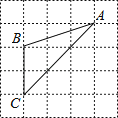 A、 B、 C、 D、8. 如图,已知点A,B分别在反比例函数和的图象上,若点A是线段的中点,则k的值为( ).
A、 B、 C、 D、8. 如图,已知点A,B分别在反比例函数和的图象上,若点A是线段的中点,则k的值为( ).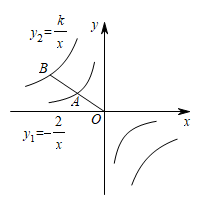 A、 B、8 C、 D、9. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( )
A、 B、8 C、 D、9. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( ) A、abc<0 B、2a+b=0 C、b2-4ac>0 D、a-b+c>010. 反比例函数与二次函数在同一平面直角坐标系中的大致图象如图所示,则它们的解析式可能分别是( )
A、abc<0 B、2a+b=0 C、b2-4ac>0 D、a-b+c>010. 反比例函数与二次函数在同一平面直角坐标系中的大致图象如图所示,则它们的解析式可能分别是( ) A、 , B、 , C、 , D、 ,
A、 , B、 , C、 , D、 ,二、填空题
-
11. 在函数 中,自变量 的取值范围是.12. 将抛物线绕它的顶点旋转后得到的抛物线解析式为 .13. 如图,中, , 顶点A,B分别在反比例函数与的图象上,则的度数为 .
 14. 二次函数y=(a-1)x2-x+a2-1 的图象经过原点,则a的值为.15. 如图1是一台手机支架,图2是其侧面示意图, , 可分别绕点A,B转动,测量知 , .当 , 转动到 , 时,点C到 的距离为cm.(结果保留小数点后一位,参考数据: , )
14. 二次函数y=(a-1)x2-x+a2-1 的图象经过原点,则a的值为.15. 如图1是一台手机支架,图2是其侧面示意图, , 可分别绕点A,B转动,测量知 , .当 , 转动到 , 时,点C到 的距离为cm.(结果保留小数点后一位,参考数据: , )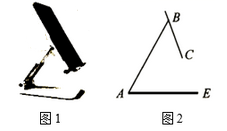 16. 已知 , , , , 是抛物线上的点,则 , , 的大小关系是(用“<”连接).
16. 已知 , , , , 是抛物线上的点,则 , , 的大小关系是(用“<”连接).三、解答题
-
17. 计算:(1)、(2)、已知为锐角, , 计算的值.18. 如图,一次函数的图形与反比例函数的图象交于点P,点P在第一象限,轴于点A,一次函数的图象分别交x轴、y轴于点C、D,且 , .
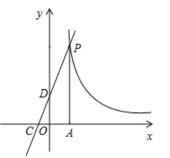 (1)、求点D的坐标;(2)、求一次函数与反比例函数的解析式;(3)、根据图象直接写出当时,一次函数值大于等于反比例函数的值时x的取值范围.19. 已知二次函数 .(1)、求顶点坐标轴和对称轴,并画出函数图象.(2)、当时方程有解,请根据图像直接写出t的取值范围.20. 如图中是抛物线形拱桥,P处有一照明灯,水面宽 , 从O、A两处观测P处,仰角分别为、 . 且 , , 以O为原点,OA所在直线为x轴建立直角坐标系.若水面上升 , 水面宽为多少?
(1)、求点D的坐标;(2)、求一次函数与反比例函数的解析式;(3)、根据图象直接写出当时,一次函数值大于等于反比例函数的值时x的取值范围.19. 已知二次函数 .(1)、求顶点坐标轴和对称轴,并画出函数图象.(2)、当时方程有解,请根据图像直接写出t的取值范围.20. 如图中是抛物线形拱桥,P处有一照明灯,水面宽 , 从O、A两处观测P处,仰角分别为、 . 且 , , 以O为原点,OA所在直线为x轴建立直角坐标系.若水面上升 , 水面宽为多少?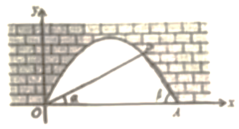 21. 如图,防洪大堤的横断面是梯形,背水坡AB的坡度i=1: ,且AB=20m.身高为1.7m的小明站在大堤A点,测得高压电线杆顶端点D的仰角为30°.已知地面CB宽30m,求小明到电线杆的距离和高压电线杆CD的高度(结果保留根号).
21. 如图,防洪大堤的横断面是梯形,背水坡AB的坡度i=1: ,且AB=20m.身高为1.7m的小明站在大堤A点,测得高压电线杆顶端点D的仰角为30°.已知地面CB宽30m,求小明到电线杆的距离和高压电线杆CD的高度(结果保留根号). 22. 某市政府大力扶持大学生创业,李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,如果以单价26元销售,那么一个月内可售出240台.根据销售经验,提高销售单价会导致销售量减少,即销售单价每提高1,销售量相应减少10台.根据物价部门规定,这种护眼台灯的销售单价不得低于进价且不得高于32元.(1)、求每月销售量y(件)与销售单价x(元)之间的函数关系式(2)、设李明每月获得利润为w(元),当销售单价定为多少元时每月可获得最大利润,每月最大利润是多少?(3)、如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?(4)、如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)23. 如图,抛物线与x轴交于两点(在的左边),与y轴交于C,;双曲线经过抛物线的顶点 , 点的横坐标为1.
22. 某市政府大力扶持大学生创业,李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,如果以单价26元销售,那么一个月内可售出240台.根据销售经验,提高销售单价会导致销售量减少,即销售单价每提高1,销售量相应减少10台.根据物价部门规定,这种护眼台灯的销售单价不得低于进价且不得高于32元.(1)、求每月销售量y(件)与销售单价x(元)之间的函数关系式(2)、设李明每月获得利润为w(元),当销售单价定为多少元时每月可获得最大利润,每月最大利润是多少?(3)、如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?(4)、如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)23. 如图,抛物线与x轴交于两点(在的左边),与y轴交于C,;双曲线经过抛物线的顶点 , 点的横坐标为1. (1)、求抛物线和双曲线的解析式.(2)、点P为抛物线上一动点,且在第一象限,连接 , 求当四边形取得最大值时,点P的坐标,并求出这个最大值.(3)、若在此抛物线和双曲线上存在点Q,使得 , 请求出点Q的坐标.
(1)、求抛物线和双曲线的解析式.(2)、点P为抛物线上一动点,且在第一象限,连接 , 求当四边形取得最大值时,点P的坐标,并求出这个最大值.(3)、若在此抛物线和双曲线上存在点Q,使得 , 请求出点Q的坐标.