山东省烟台市牟平区2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-12-20 类型:期中考试
一、单选题
-
1. 计算的值( )A、3 B、1 C、 D、2. 已知二次函数y=2x2−4x−1在0≤x≤a时,y取得的最大值为15,则a的值为( )A、1 B、2 C、3 D、43. 将 的各边长都缩小为原来的 , 则锐角A的正弦值( )A、缩小为原来的 B、不变 C、扩大为原来的倍 D、缩小为原来的4. 小嘉说:将二次函数 的图象平移或翻折后经过点 有4种方法:
①向右平移2个单位长度 ②向右平移1个单位长度,再向下平移1个单位长度③向下平移4个单位长度④沿x轴翻折,再向上平移4个单位长度
你认为小嘉说的方法中正确的个数有( )
A、1个 B、2个 C、3个 D、4个5. 用科学计算器求的值,按键顺序正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 在平面直角坐标系中,将抛物线y=x2﹣(m﹣1)x+m(m>1)沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图,点A,B,C在正方形网格的格点上,则sin∠BAC=( )
6. 在平面直角坐标系中,将抛物线y=x2﹣(m﹣1)x+m(m>1)沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图,点A,B,C在正方形网格的格点上,则sin∠BAC=( )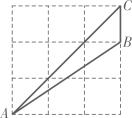 A、 B、 C、 D、8. 如图,坡角为α的斜坡上有一棵垂直于水平地面的大树AB,当太阳光线与水平线成45°角沿斜坡照下,在斜坡上的树影BC长为m,则大树AB的高为( )
A、 B、 C、 D、8. 如图,坡角为α的斜坡上有一棵垂直于水平地面的大树AB,当太阳光线与水平线成45°角沿斜坡照下,在斜坡上的树影BC长为m,则大树AB的高为( )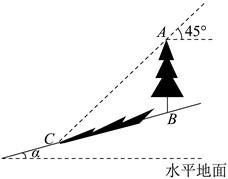 A、 B、 C、 D、9. 抛物线上部分点的横坐标x,纵坐标y的对应值如表:
A、 B、 C、 D、9. 抛物线上部分点的横坐标x,纵坐标y的对应值如表:x
-2
-1
0
1
y
0
4
6
6
下列结论错误的是( )
A、抛物线的开口向下 B、抛物线的对称轴为直线 C、抛物线与x轴的一个交点坐标为 D、函数的最大值为10. 根据如图所示的二次函数的图象,判断反比例函数与一次函数的图象大致是( )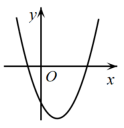 A、
A、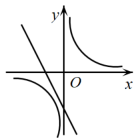 B、
B、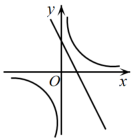 C、
C、 D、
D、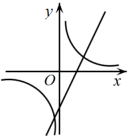 11. 数学活动小组到某广场测量标志性建筑AB的高度.如图,他们在地面上C点测得最高点A的仰角为22°,再向前70m至D点,又测得最高点A的仰角为58°,点C,D,B在同一直线上,则该建筑物AB的高度约为( )(精确到1m.参考数据: , , , )
11. 数学活动小组到某广场测量标志性建筑AB的高度.如图,他们在地面上C点测得最高点A的仰角为22°,再向前70m至D点,又测得最高点A的仰角为58°,点C,D,B在同一直线上,则该建筑物AB的高度约为( )(精确到1m.参考数据: , , , )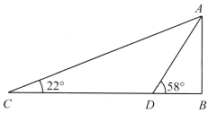 A、28m B、34m C、37m D、46m12. 在平面直角坐标系中,已知二次函数的图象如图所示,有下列5个结论:①;②;③;④;⑤.其中正确的有( )
A、28m B、34m C、37m D、46m12. 在平面直角坐标系中,已知二次函数的图象如图所示,有下列5个结论:①;②;③;④;⑤.其中正确的有( )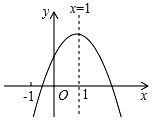 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 抛物线 ( 为常数)与x轴交点的个数是 .14. 如图,在中, , 点D为边的中点,连接 , 若 , , 则的值为 .
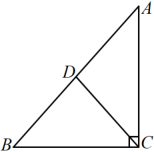 15. 如图,某一时刻太阳光从窗户射入房间内,与地面的夹角 , 已知窗户的高度 , 窗台的高度 , 窗外水平遮阳篷的宽 , 则的长度为(结果精确到).
15. 如图,某一时刻太阳光从窗户射入房间内,与地面的夹角 , 已知窗户的高度 , 窗台的高度 , 窗外水平遮阳篷的宽 , 则的长度为(结果精确到). 16. 抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,其与x轴的一个交点坐标为(﹣3,0),对称轴为x=﹣1,则当y<0时,x的取值范围是.
16. 抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,其与x轴的一个交点坐标为(﹣3,0),对称轴为x=﹣1,则当y<0时,x的取值范围是.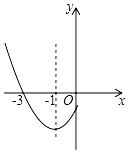 17. 如图,有甲乙两座建筑物,从甲建筑物点处测得乙建筑物点的俯角为 , 点的俯角为 , 为两座建筑物的水平距离.已知乙建筑物的高度为 , 则甲建筑物的高度为.( , , , 结果保留整数).
17. 如图,有甲乙两座建筑物,从甲建筑物点处测得乙建筑物点的俯角为 , 点的俯角为 , 为两座建筑物的水平距离.已知乙建筑物的高度为 , 则甲建筑物的高度为.( , , , 结果保留整数).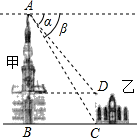 18. 小明在学习“二次函数”内容后,进行了反思总结.如图,二次函数y=ax2+bx+c(a≠0)图像的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图像他得出下列结论:①ab>0且c>0;②a+b+c=0;③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为﹣3和1;④若点(﹣4,y1),(﹣2,y2),(3,y3)均在二次函数图象上,则y1<y2<y3;⑤3a+c<0,其中正确的结论有 . (填序号,多选、少选、错选都不得分)
18. 小明在学习“二次函数”内容后,进行了反思总结.如图,二次函数y=ax2+bx+c(a≠0)图像的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图像他得出下列结论:①ab>0且c>0;②a+b+c=0;③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为﹣3和1;④若点(﹣4,y1),(﹣2,y2),(3,y3)均在二次函数图象上,则y1<y2<y3;⑤3a+c<0,其中正确的结论有 . (填序号,多选、少选、错选都不得分)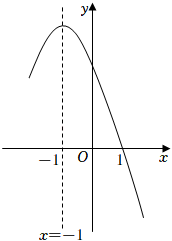
三、解答题
-
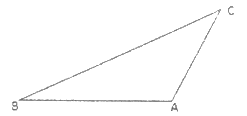
19. 如图,在中, , , , 求的长.( , )
 20. 小红看到一处喷水景观,喷出的水柱呈抛物线形状,她对此展开研究:测得喷水头P距地面0.7m,水柱在距喷水头P水平距离5m处达到最高,最高点距地面3.2m;建立如图所示的平面直角坐标系,并设抛物线的表达式为 ,其中x(m)是水柱距喷水头的水平距离,y(m)是水柱距地面的高度.
20. 小红看到一处喷水景观,喷出的水柱呈抛物线形状,她对此展开研究:测得喷水头P距地面0.7m,水柱在距喷水头P水平距离5m处达到最高,最高点距地面3.2m;建立如图所示的平面直角坐标系,并设抛物线的表达式为 ,其中x(m)是水柱距喷水头的水平距离,y(m)是水柱距地面的高度.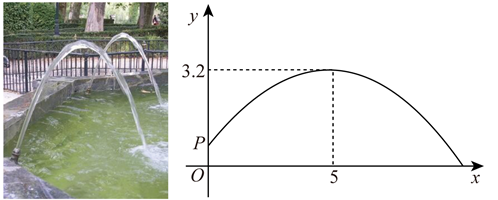 (1)、求抛物线的表达式.(2)、爸爸站在水柱正下方,且距喷水头P水平距离3m,身高1.6m的小红在水柱下方走动,当她的头顶恰好接触到水柱时,求她与爸爸的水平距离.21. 小华同学将笔记本电脑水平放置在桌子上,当是示屏的边缘线 与底板的边缘线 所在水平线的夹角为120°时,感觉最舒适(如图①).侧面示意图为图②;使用时为了散热,他在底板下面垫入散热架,如图③,点B、O、C在同一直线上, , , .
(1)、求抛物线的表达式.(2)、爸爸站在水柱正下方,且距喷水头P水平距离3m,身高1.6m的小红在水柱下方走动,当她的头顶恰好接触到水柱时,求她与爸爸的水平距离.21. 小华同学将笔记本电脑水平放置在桌子上,当是示屏的边缘线 与底板的边缘线 所在水平线的夹角为120°时,感觉最舒适(如图①).侧面示意图为图②;使用时为了散热,他在底板下面垫入散热架,如图③,点B、O、C在同一直线上, , , .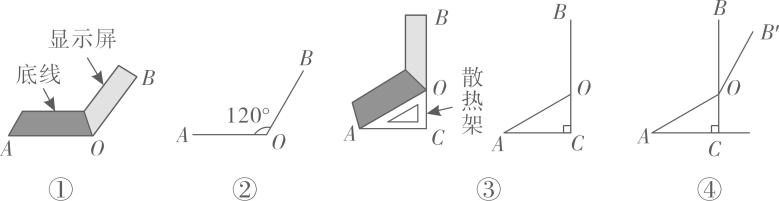 (1)、求 的长;(2)、如图④,垫入散热架后,要使显示屏的边缘线 与水平线的夹角仍保持120°,求点 到 的距离.(结果保留根号)22. 打油茶是广西少数民族特有的一种民俗,某特产公司近期销售一种盒装油茶,每盒的成本价为50元,经市场调研发现,该种油茶的月销售量y(盒)与销售单价x(元)之间的函数图象如图所示.
(1)、求 的长;(2)、如图④,垫入散热架后,要使显示屏的边缘线 与水平线的夹角仍保持120°,求点 到 的距离.(结果保留根号)22. 打油茶是广西少数民族特有的一种民俗,某特产公司近期销售一种盒装油茶,每盒的成本价为50元,经市场调研发现,该种油茶的月销售量y(盒)与销售单价x(元)之间的函数图象如图所示.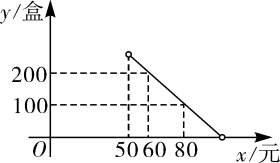 (1)、求y与x的函数解析式,并写出自变量x的取值范围;(2)、当销售单价定为多少元时,该种油茶的月销售利润最大?求出最大利润.23. 2022年北京冬奥会的成功举办激发了人们对冰雪运动的热情.如图是某滑雪场的横截面示意图,雪道分为AB,BC两部分,小明同学在C点测得雪道BC的坡度i=1:2.4,在A点测得B点的俯角∠DAB=30°.若雪道AB长为270m,雪道BC长为260m.
(1)、求y与x的函数解析式,并写出自变量x的取值范围;(2)、当销售单价定为多少元时,该种油茶的月销售利润最大?求出最大利润.23. 2022年北京冬奥会的成功举办激发了人们对冰雪运动的热情.如图是某滑雪场的横截面示意图,雪道分为AB,BC两部分,小明同学在C点测得雪道BC的坡度i=1:2.4,在A点测得B点的俯角∠DAB=30°.若雪道AB长为270m,雪道BC长为260m.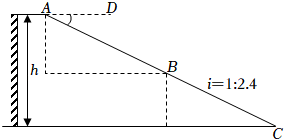 (1)、求该滑雪场的高度h;(2)、据了解,该滑雪场要用两种不同的造雪设备来满足对于雪量和雪质的不同要求,其中甲设备每小时造雪量比乙设备少35m3 , 且甲设备造雪150m3所用的时间与乙设备造雪500m3所用的时间相等.求甲、乙两种设备每小时的造雪量.24. 如图,抛物线(b,c是常数)的顶点为C,与x轴交于A,B两点, , , 点P为线段上的动点,过P作//交于点Q.
(1)、求该滑雪场的高度h;(2)、据了解,该滑雪场要用两种不同的造雪设备来满足对于雪量和雪质的不同要求,其中甲设备每小时造雪量比乙设备少35m3 , 且甲设备造雪150m3所用的时间与乙设备造雪500m3所用的时间相等.求甲、乙两种设备每小时的造雪量.24. 如图,抛物线(b,c是常数)的顶点为C,与x轴交于A,B两点, , , 点P为线段上的动点,过P作//交于点Q.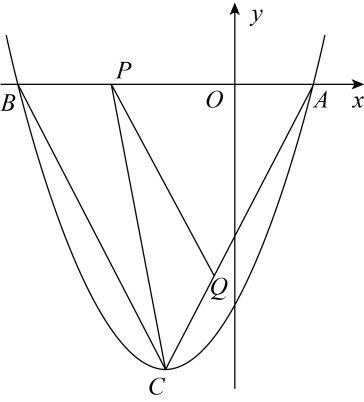 (1)、求该抛物线的解析式;(2)、求面积的最大值,并求此时P点坐标.25. 如图,在直角坐标系中,二次函数的图象与x轴交于A,B两点,与y轴交于点 , 对称轴为直线 , 顶点为点D.
(1)、求该抛物线的解析式;(2)、求面积的最大值,并求此时P点坐标.25. 如图,在直角坐标系中,二次函数的图象与x轴交于A,B两点,与y轴交于点 , 对称轴为直线 , 顶点为点D.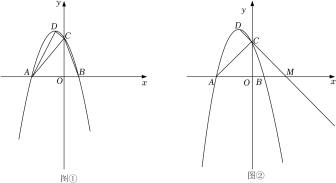 (1)、求二次函数的表达式;(2)、连接DA,DC,CB,CA,如图①所示,求证:;(3)、如图②,延长DC交x轴于点M,平移二次函数的图象,使顶点D沿着射线DM方向平移到点且 , 得到新抛物线 , 交y轴于点N.如果在的对称轴和上分别取点P,Q,使以MN为一边,点M,N,P,Q为顶点的四边形是平行四边形,求此时点Q的坐标.
(1)、求二次函数的表达式;(2)、连接DA,DC,CB,CA,如图①所示,求证:;(3)、如图②,延长DC交x轴于点M,平移二次函数的图象,使顶点D沿着射线DM方向平移到点且 , 得到新抛物线 , 交y轴于点N.如果在的对称轴和上分别取点P,Q,使以MN为一边,点M,N,P,Q为顶点的四边形是平行四边形,求此时点Q的坐标.