山东省潍坊市寒亭区2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-12-20 类型:期中考试
一、单选题
-
1. 下列圆中既有圆心角又有圆周角的是( ).A、
 B、
B、 C、
C、 D、
D、 2. 若用我们数学课本上采用的科学计算器计算 , 按键顺序正确的是( )A、
2. 若用我们数学课本上采用的科学计算器计算 , 按键顺序正确的是( )A、 B、
B、 C、
C、 D、
D、 3. 如图,已知四边形四边形 , , , 则的长是( ).
3. 如图,已知四边形四边形 , , , 则的长是( ).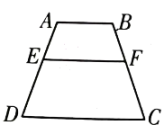 A、6 B、 C、 D、44. 如图,的直径与弦交于点E,若B为的中点,则下列说法错误的是( ).
A、6 B、 C、 D、44. 如图,的直径与弦交于点E,若B为的中点,则下列说法错误的是( ). A、 B、 C、 D、5. 苏州虎丘塔是我国江南著名的园林景点. 它建成于宋代(961年),共7层,高h米. 由于地基的原因,塔身自400年前就开始向西北方向倾斜. 据测量,至今塔顶的中心偏离底层中心铅垂线的角度为 , 被称为“东方比萨斜塔”. 如今虎丘塔塔顶的中心偏离底层中心铅垂线的距离是( )米
A、 B、 C、 D、5. 苏州虎丘塔是我国江南著名的园林景点. 它建成于宋代(961年),共7层,高h米. 由于地基的原因,塔身自400年前就开始向西北方向倾斜. 据测量,至今塔顶的中心偏离底层中心铅垂线的角度为 , 被称为“东方比萨斜塔”. 如今虎丘塔塔顶的中心偏离底层中心铅垂线的距离是( )米 A、 B、 C、 D、6. 已知点在第四象限,则关于x的一元二次方程的根的情况是( ).A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定7. 课下小亮和小莹讨论一道题目:“已知点O是的外心, , 求”.小亮的解答为:如图,画以及它的外接圆O,连接 , 由 , 得 . 而小莹说:“小亮考虑的不周全,应该还有另一个不同的值”.下列判断正确的是( )
A、 B、 C、 D、6. 已知点在第四象限,则关于x的一元二次方程的根的情况是( ).A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定7. 课下小亮和小莹讨论一道题目:“已知点O是的外心, , 求”.小亮的解答为:如图,画以及它的外接圆O,连接 , 由 , 得 . 而小莹说:“小亮考虑的不周全,应该还有另一个不同的值”.下列判断正确的是( )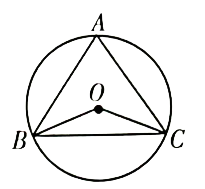 A、小亮求的结果不对,应该是 B、小莹说的不对,就是 C、小莹说的对,的另一个值是 D、两人说的都不对,的值有无数个8. 一个容器盛满纯果汁5升,第一次倒出一部分果汁后加满水,第二次又倒出同样体积稀释过的果汁,再加满水,此时容器中的纯果汁剩下4升.设每次倒出x升,根据题意列出的方程是( )A、 B、 C、 D、
A、小亮求的结果不对,应该是 B、小莹说的不对,就是 C、小莹说的对,的另一个值是 D、两人说的都不对,的值有无数个8. 一个容器盛满纯果汁5升,第一次倒出一部分果汁后加满水,第二次又倒出同样体积稀释过的果汁,再加满水,此时容器中的纯果汁剩下4升.设每次倒出x升,根据题意列出的方程是( )A、 B、 C、 D、二、多选题
-
9. 在方格纸(每个小正方形的边长为1)上的位置如图所示,顶点都在格点上,交于点D,D在格线上,下列选项中正确的是( )
 A、 B、 C、 D、10. 如图,点B,C在x轴上,点A和D的纵坐标分别为2, , 连接与交于点E, , 下列选项中正确的是( )
A、 B、 C、 D、10. 如图,点B,C在x轴上,点A和D的纵坐标分别为2, , 连接与交于点E, , 下列选项中正确的是( ) A、 B、 C、 D、11. 直角三角形斜边的长为15,两条直角边的差为5.如果要求两条直角边的长,可以设较短的直角边的长为x,从而列出方程: . 在估计这个方程的正实数根时,下列说法正确的是( ).A、该方程有一个正实数根 B、可以估计x的范围是 C、可以估计x的范围是 D、可以估计x的范围是12. 如图,是半圆的直径,C是半圆弧的中点,D是的中点,下列结论中正确的是( )
A、 B、 C、 D、11. 直角三角形斜边的长为15,两条直角边的差为5.如果要求两条直角边的长,可以设较短的直角边的长为x,从而列出方程: . 在估计这个方程的正实数根时,下列说法正确的是( ).A、该方程有一个正实数根 B、可以估计x的范围是 C、可以估计x的范围是 D、可以估计x的范围是12. 如图,是半圆的直径,C是半圆弧的中点,D是的中点,下列结论中正确的是( )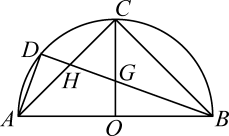 A、 B、 C、 D、
A、 B、 C、 D、三、填空题
-
13. 若是关于x的一元二次方程,则m= .14. 如图,小亮测得学校门口栏杆的短臂长1米,长臂长4米,当短臂外端A下降0.6米时,长臂外端B升高米.
 15. 如图,小莹沿一条笔直的小路自西向东步行,小莹在A处测得旗杆C在北偏东方向,30分钟后小莹到达B处,测得旗杆C在北偏西方向,小莹在这条小路上离旗杆最近的距离是1000米,则小莹步行的速度为米/分钟.(参考数据:)
15. 如图,小莹沿一条笔直的小路自西向东步行,小莹在A处测得旗杆C在北偏东方向,30分钟后小莹到达B处,测得旗杆C在北偏西方向,小莹在这条小路上离旗杆最近的距离是1000米,则小莹步行的速度为米/分钟.(参考数据:) 16. 如图,某古城大门口的平面图上方是半圆,下方是矩形,有一辆装货后宽3米的货车从大门中间进入古城,那么货车装货后的最大高度为米.
16. 如图,某古城大门口的平面图上方是半圆,下方是矩形,有一辆装货后宽3米的货车从大门中间进入古城,那么货车装货后的最大高度为米.
四、解答题
-
17.(1)、计算式子的值;(2)、根据要求解下列一元二次方程:
①(配方法);
②(因式分解法).
18. 如图,在直角坐标系中,的顶点坐标分别为 . (1)、请在图中标出外接圆的圆心C,并写出点C的坐标.(2)、在直角坐标系的第三象限,画出以点O为位似中心,与位似的图形,使它与的相似比为 , 并写出点A,B对应点的坐标.19. 用反证法证明:一个三角形中不能有两个角是直角.
(1)、请在图中标出外接圆的圆心C,并写出点C的坐标.(2)、在直角坐标系的第三象限,画出以点O为位似中心,与位似的图形,使它与的相似比为 , 并写出点A,B对应点的坐标.19. 用反证法证明:一个三角形中不能有两个角是直角.已知: , , 是的三个内角.
求证: , , 中不能有两个角是直角.
20. 已知关于x的一元二次方程 .(1)、求证:该方程总有两个实数根;(2)、方程的两个实数根满足 , 求实数m的值.21. 内接于 , D,F分别是与上的点, . 连接并延长交的延长线于点E,连接 . (1)、求证:;(2)、若为边长等于6的等边三角形,且 . 求 .22. 如图,小亮站在池塘边,看到水中点A处有一装饰灯,由于光的折射,这个装饰灯的实际位置在点B处,的延长线垂直于水面l,垂足为点C.装饰灯射入小亮眼中的光线与水面l的交点为O,入射角为 , 折射角为 , 法线为 , 已知装饰灯到水面的距离为m,求点A与点B之间的距离.(用含字母m, , 的式子表示)
(1)、求证:;(2)、若为边长等于6的等边三角形,且 . 求 .22. 如图,小亮站在池塘边,看到水中点A处有一装饰灯,由于光的折射,这个装饰灯的实际位置在点B处,的延长线垂直于水面l,垂足为点C.装饰灯射入小亮眼中的光线与水面l的交点为O,入射角为 , 折射角为 , 法线为 , 已知装饰灯到水面的距离为m,求点A与点B之间的距离.(用含字母m, , 的式子表示) 23. 今年以来,某市接待游客人数逐月增加,据统计,八月份和十月份到某景区游玩的游客人数分别为4万人和5.76万人.(1)、求八月到十月该景区游客人数平均每月的增长率;(2)、若该景区仅有A,B两个景点,售票处出示的三种购票方式如表所示:
23. 今年以来,某市接待游客人数逐月增加,据统计,八月份和十月份到某景区游玩的游客人数分别为4万人和5.76万人.(1)、求八月到十月该景区游客人数平均每月的增长率;(2)、若该景区仅有A,B两个景点,售票处出示的三种购票方式如表所示:购票方式
甲
乙
丙
可游玩景点
A
B
A和B
门票价格
100元/人
80元/人
160元/人
据预测,十一月份选择甲、乙、丙三种购票方式的人数分别有2万人、3万人和2万人,并且当甲、乙两种门票价格不变时,丙种门票价格每下降1元,将有600名原计划购买甲种门票的游客和400名原计划购买乙种门票的游客改为购买丙种门票.设十一月份景区门票总收入为W万元,丙种门票下降m元,请写出W与m之间的表达式,并求出要想让十一月份门票总收入达到798万元,丙种门票应该下降多少元?
24. 【阅读理解】:如图,在中,a,b,c分别是 , , 的对边, , 其外接圆半径为R.根据锐角三角函数的定义: , , 可得 , 即(规定). (1)、【探究活动】:如图,在锐角中,a,b,c分别是 , , 的对边,其外接圆半径为R,那么:(用>,=或<连接),并说明理由 .
(1)、【探究活动】:如图,在锐角中,a,b,c分别是 , , 的对边,其外接圆半径为R,那么:(用>,=或<连接),并说明理由 .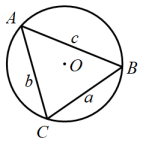 (2)、【初步应用】:事实上,以上结论适用于任意三角形.在中,a,b,c分别是 , , 的对边.已知 , , , 求 .(3)、【综合应用】:如图,在某次数学实践活动中,小莹同学测量一栋楼的高度,在A处用测角仪测得地面点C处的俯角为45°,点D处的俯角为15°,B,C,D在一条直线上,且C,D两点的距离为100m,求楼的高度.(参考数据: , )
(2)、【初步应用】:事实上,以上结论适用于任意三角形.在中,a,b,c分别是 , , 的对边.已知 , , , 求 .(3)、【综合应用】:如图,在某次数学实践活动中,小莹同学测量一栋楼的高度,在A处用测角仪测得地面点C处的俯角为45°,点D处的俯角为15°,B,C,D在一条直线上,且C,D两点的距离为100m,求楼的高度.(参考数据: , )