山东省威海市环翠区2022-2023学年九年级上学期期中数学试题

试卷更新日期：2022-12-20 类型：期中考试

进入出卷网下载

一、单选题

1. 反比例函数y＝ $\frac{1}{x}$ （x＜0）的图象位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 如图，在 $4 \times 5$ 的正方形网格中，每个小正方形的边长都是1， $△ A B C$ 的顶点都在这些小正方形的顶点上，那么 $\sin ∠ A C B$ 的值为（）．

A、 $\frac{3 \sqrt{5}}{5}$ B、 $\frac{\sqrt{17}}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
3. 如图，点A是反比例函数y $= \frac{6}{x}$ （x＞0）上的一点，过点A作AC⊥y轴，垂足为点C，AC交反比例函数y＝ $\frac{2}{x}$ 的图象于点B，点P是x轴上的动点，则△PAB的面积为（）

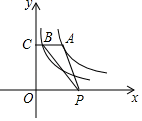A、2 B、4 C、6 D、8

查看试题解析
4. 如图，在离铁塔150米的A处，用测倾仪测得塔顶的仰角为α，测倾仪高AD为1.5米，则铁塔的高BC为（）

A、(1.5+150tanα) 米 B、(1.5+ $\frac{150}{\tan α}$ )米 C、(1.5+150sinα)米 D、(1.5+ $\frac{150}{\sin α}$ )米

查看试题解析
5. 如图，在矩形ABCD中，点E在DC上，将矩形沿AE折叠，使点D落在BC边上的点F处．若AB＝3，BC＝5，则tan∠DAE的值为（）

A、 $\frac{1}{2}$ B、 $\frac{9}{20}$ C、 $\frac{2}{5}$ D、 $\frac{1}{3}$

查看试题解析
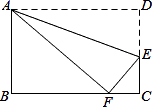6. 关于二次函数 $y = \frac{1}{4} x^{2} - 6 x + a + 27$ ，下列说法错误的是（）

A、若将图象向上平移10个单位，再向左平移2个单位后过点 $(4, 5)$ ，则 $a = - 5$ B、当 $x = 12$ 时，y有最小值 $a - 9$ C、 $x = 2$ 对应的函数值比最小值大7 D、当 $a < 0$ 时，图象与x轴有两个不同的交点

查看试题解析
7. 已知点（﹣2，a），（2，b），（3，c）在函数y＝ $\frac{k}{x}$ （k＞0）的图象上，则下列判断正确的是（　　）

A、a＜b＜c B、b＜a＜c C、a＜c＜b D、c＜b＜a

查看试题解析
8. 二次函数y=x²的图象平移后经过点（2，0），则下列平移方法正确的是（　　）

A、向左平移2个单位，向下平移2个单位 B、向左平移1个单位，向上平移2个单位 C、向右平移1个单位，向下平移1个单位 D、向右平移2个单位，向上平移1个单位

查看试题解析
9. 如图，一座厂房屋顶人字架的跨度 $A C = 12 cm$ ，上弦 $A B = B C$ ， $∠ B A C = 25 °$ .若用科学计算器求上弦AB的长，则下列按键顺序正确的是（）

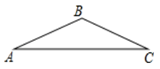A、 $6 \div \cos 25 =$ B、 $6 \times \sin 25 =$ C、 $6 \div \tan 25 =$ D、 $12 \div \cos 25 =$

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c$ 的图像如图所示，反比例函数 $y = \frac{a}{x}$ 与正比例函数 $y = b x$ 在同一坐标系内的大致图像是（）

A、 B、 C、 D、

查看试题解析
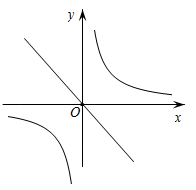11. 如图，在直角坐标系中，以坐标原点 $O (0 ， 0) ， A (0 ， 4) ， B (3 ， 0)$ 为顶点的 $R t △ A O B$ ，其两个锐角对应的外角角平分线相交于点P，且点P恰好在反比例函数 $y = \frac{k}{x}$ 的图象上，则P点的横坐标为（）

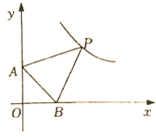A、5 B、6 C、7 D、8

查看试题解析
12. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，有下列结论① $b^{2} - 4 a c > 0$ ；② $a b c > 0$ ；③ $8 a + c > 0$ ；④ $9 a + 3 b + c < 0$ 其中，正确结论的个数是（）

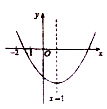A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 点A（a，b）是一次函数y=x﹣2与反比例函数y= $\frac{4}{x}$ 的交点，则a²b﹣ab²= ．

查看试题解析
14. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，点D为 $A B$ 边的中点，连接 $C D$ ，若 $B C = 4$ ， $C D = 3$ ，则 $\cos ∠ D C B$ 的值为．

查看试题解析
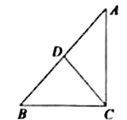15. 已知函数y₁＝﹣（m+1）x²+nx+2与y₂＝mx+2的图象都经过A（4，﹣4）．若y₂≤y₁ ，则x的取值范围为．

查看试题解析
16. 如图，海上有一灯塔P，位于小岛A北偏东60°方向上，一艘轮船从北小岛A出发，由西向东航行 $24nmile$ 到达B处，这时测得灯塔P在北偏东30°方向上，如果轮船不改变航向继续向东航行，当轮船到达灯塔P的正南方，此时轮船与灯塔P的距离是 $n mile$ .（结果保留一位小数， $\sqrt{3} \approx 1.73$ ）

查看试题解析
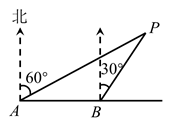17. 竖直向上抛出小球的高度h（米）与抛出的时间t（秒）满足关系式 $h = - 4.9 t^{2} + 24.5 t$ ，从地面相隔1秒竖直向上分别抛出的两个小球，当两个小球在空中处于同一个高度时，这个高度离地面米．

查看试题解析
18. 下列关于二次函数 $y = - {(x - m)}^{2} + m^{2} + 1$ （ $m$ 为常数）的结论，①该函数的图象与函数 $y = - x^{2}$ 的图象形状相同；②该函数的图象一定经过点 $(0, 1)$ ；③当 $x > 0$ 时，y随x的增大而减小；④该函数的图象的顶点在函数 $y = x^{2} + 1$ 的图像上，其中所有正确的结论序号是.

查看试题解析

三、解答题

19. 计算： ${(2022 - π)}^{0} - 4 c o s 30 ° + 4 t a n 45 ° - | 3 - \sqrt{12} |$

查看试题解析
20. 如图，B，C是反比例函数y= $\frac{k}{x}$ （k≠0）在第一象限图象上的点，过点B的直线y=x-1与x轴交于点A，CD⊥x轴，垂足为D，CD与AB交于点E，OA=AD，CD=3.

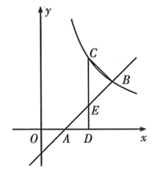(1)、求此反比例函数的表达式；

(2)、求△BCE的面积.

查看试题解析
21. 某农场计划建造一个矩形养殖场，为充分利用现有资源，该矩形养殖场一面靠墙（墙的长度为10m），另外三面用栅栏围成，中间再用栅栏把它分成两个面积为1：2的矩形，已知栅栏的总长度为24m，设较小矩形的宽为xm（如图）.

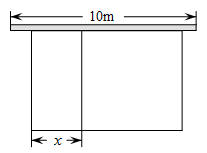(1)、若矩形养殖场的总面积为36 $m^{2}$ ，求此时x的值；

(2)、当x为多少时，矩形养殖场的总面积最大？最大值为多少？

查看试题解析
22. 如图，三角形花园 $A B C$ 紧邻湖泊，四边形 $A B D E$ 是沿湖泊修建的人行步道．经测量，点C在点A的正东方向， $A C = 200$ 米．点E在点A的正北方向．点B，D在点C的正北方向， $B D = 100$ 米．点B在点A的北偏东 $30 °$ ，点D在点E的北偏东 $45 °$ ．

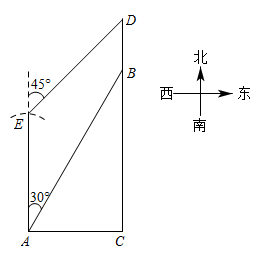(1)、求步道 $D E$ 的长度（精确到个位）；

(2)、点D处有直饮水，小红从A出发沿人行步道去取水，可以经过点B到达点D，也可以经过点E到达点D．请计算说明他走哪一条路较近？（参考数据： $\sqrt{2} \approx 1.4$ ， $\sqrt{3} \approx 1.7$ ）

查看试题解析