山东省青岛市崂山区2022-2023学年九年级上学期期中数学试题

试卷更新日期：2022-12-20 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式中是一元二次方程的是（）

A、 $x^{2} + x = 2 y$ B、 $x^{2} = 1$ C、 $a x^{2} + b x + c = 0$ D、 $x^{2} + x + 1$

查看试题解析
2. 如图，在菱形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点O，E为 $A D$ 边的中点， $A B =6$ ，则 $O E$ 的长为（）．

A、2 B、3 C、6 D、12

查看试题解析
3. 已知 $x = - 1$ 是关于x的一元二次方程 $x^{2} + k x - 2 = 0$ 的一个根，则k的值为（）

A、1 B、 $- 1$ C、2 D、 $- 2$

查看试题解析
4. 学校团委举行“感动校园十大人物”颁奖活动，某班决定从甲、乙、丙、丁四人中随机派两名代表参加此活动，则甲、乙两人恰有一人参加此活动的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{5}{6}$ C、 $\frac{1}{6}$ D、 $\frac{1}{2}$

查看试题解析
5. 如图，一张长方形纸板长40cm，宽30cm，剪掉2个小正方形和2个小长方形（阴影部分即剪掉部分），剩余的部分可折成一个有盖的长方体纸盒，若纸盒底面ABCD的面积等于300 $c m^{2}$ ，设剪掉的小正方形边长为x cm，则根据题意可得方程（　　）

A、 $(20 - x) (30 - 2 x) = 300$ B、 $(20 - x) (30 - x) = 300$ C、 $(20 - 2 x) (30 - x) = 300$ D、 $(20 - 2 x) (30 - 2 x) = 300$

查看试题解析
6. 如图，矩形ABCD的对角线AC、BD相交于点O，∠AOB=120°， $C E ∥ B D$ ， $D E ∥ A C$ ，若AD=2，则四边形CODE的周长为（）

A、12 B、10 C、8 D、4

查看试题解析
7. 如图，在某一时刻测得1米长的竹竿竖直放置时影长1.2米，在同一时刻旗杆AB的影长不全落在水平地面上，有一部分落在楼房的墙上，他测得落在地面上影长为BD＝9.6米，留在墙上的影长CD＝2米，则旗杆的高度（　　）

A、9米 B、9.6米 C、10米 D、10.2米

查看试题解析
8. 如图，在正方形 $A B C D$ 中，E为 $A D$ 上一点，连接 $B E$ ， $B E$ 交对角线 $A C$ 于点F，连接 $D F$ ，若 $∠ A B E = 30 °$ ，则 $∠ C F D$ 的度数为（）．

A、 $45 °$ B、 $70 °$ C、 $75 °$ D、 $80 °$

查看试题解析

二、填空题

9. 关于 $x$ 的方程 $x^{2} + x - 2 = 0$ 的两个实数根为 $x_{1}$ ， $x_{2}$ ，则 $x_{1}^{2} + x_{2}^{2} =$ ．

查看试题解析
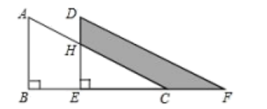
10. 在一个不透明的袋中装有若干个红球和4个黑球，每个球除颜色外完全相同．摇匀后从中摸出一个球，记下颜色后再放回袋中．不断重复这一过程，共摸球100次．其中有40次摸到黑球，估计袋中红球的个数是．

查看试题解析
11. 如图，两个直角三角形重叠在一起，将其中一个沿点B到点C的方向平移到 $Δ D E F$ 的位置， $A B = 10$ ， $D H = 4$ ，平移距离为6，则阴影部分的面积为．

查看试题解析
12. 电影《长津湖之水门桥》讲述了一段波澜壮阔的历史，一上映就获得全国人民的追捧，某地第一天票房约2亿元，以后每天票房按相同的增长率增长，第三天票房收入达2.88亿元，若把增长率记作x，则方程可以列为.

查看试题解析
13. 用图中两个可以自由转动的转盘做“配紫色”游戏，分别转动两个转盘，若其中一个转出红色，另一个转出蓝色即可配成紫色，则配成紫色的概率是．

查看试题解析
14. 如图，已知正方形 $A B C D$ 的边长为4，P是对角线 $B D$ 上一点， $P E ⊥ B C$ 于点E， $P F ⊥ C D$ 于点F，连接 $A P$ ， $E F$ ．给出下列结论：① $P D = \sqrt{2} D F$ ；②四边形 $P E C F$ 的周长为8；③ $E F$ 的最小值为2；④ $A P ⊥ E F$ ．其中正确结论的序号为．

查看试题解析

三、解答题

15. 已知：线段a， $∠ α$ ．
求作：菱形 $A B C D$ ，使 $B C = a$ ， $∠ A B C = ∠ α$ ．

查看试题解析
16. 用适当的方法解方程

(1)、 ${(2 x - 1)}^{2} = {(3 - x)}^{2}$

(2)、 $x^{2} - 4 x - 7 = 0$ （配方法）

(3)、 $x^{2} - 5 x - 6 = 0$

(4)、已知关于x的一元二次方程 $m x^{2} - (2 m - 1) x + m - 2 = 0$ 有两个不相等的实数根．求m的取值范围．

查看试题解析
17. 一个不透明的箱子里装有3个红色小球和若干个白色小球，每个小球除颜色外其他完全相同，每次把箱子里的小球摇匀后随机摸出一个小球，记下颜色后再放回箱子里，通过大量重复实验后，发现摸到红色小球的频率稳定于0.75左右.

(1)、请你估计箱子里白色小球的个数；

(2)、现从该箱子里摸出1个小球，记下颜色后放回箱子里，摇匀后，再摸出1个小球，求两次摸出的小球颜色恰好不同的概率（用画树状图或列表的方法）.

查看试题解析
18. 如图，菱形 $A B C D$ 的对角线 $A C$ 与 $B D$ 交于点O，分别过点C、点D作 $B D$ 、 $A C$ 的平行线交于点E，连接 $E O$ 交 $C D$ 于点F．

(1)、求证：四边形 $D E C O$ 是矩形；

(2)、若 $A C = 4$ ， $B D = 6$ ，求 $E F$ 的长．

查看试题解析
19. 如图，某小区有一块长为18米，宽为6米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为60平方米，两块绿地之间及周边留有宽度相等的人行通道，求人行道的宽度为多少米？

查看试题解析
20. 已知：如图，在▱ABCD中，点E是BC的中点，连接AE并延长交DC的延长线于点F，连接BF．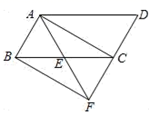

(1)、求证：△ABE≌△FCE；

(2)、若AF＝AD，判断四边形ABFC的形状，并说明理由．

查看试题解析
21. 如图，数学兴趣小组利用硬纸板自制的Rt△ABC来测量操场旗杆MN的高度，他们通过调整测量位置，并使边AC与旗杆顶点M在同一直线上，已知AC＝0.8米，BC＝0.5米，目测点A到地面的距离AD＝1.5米，到旗杆的水平距离AE＝20米，求旗杆MN的高度．

查看试题解析
22. 某超市销售一种商品，成本价为50元/千克，规定每千克售价不低于成本价，且不高于85元．经市场调查，该商品每天的销售量y（千克）与售价x（元/千克）满足一次函数关系，如图所示：

(1)、求y与x之间的函数表达式；

(2)、该商场销售这种商品要想每天获得1350元的利润，每件商品的售价应定为多少元？

查看试题解析
23.
问题提出：用n个三角形最多可以把平面分成几部分？
为了找到解决问题的办法，我们可以把上述问题简单化：

(1)、探究（一）：我们先考虑最简单的情况：用一个三角形最多可以把平面分成几部分？
①用1个三角形分平面只有一种情况，平面本身是1部分，一个三角形将平面分成三角形内和三角形外2部分，即增加1部分，所以用1个三角形最多可以把平面分成2部分．
②用2个三角形最多可以把平面分成几部分？
两个三角形不能相交时将平面分成3部分．
相交时：如图1~图6，用2个三角形分平面有6种情况：如图1，当两个三角形只有1个交点时，这两个三角形将平面分成3部分；当两个三角形有2个交点时，这两个三角形将平面分成4部分；当两个三角形有3个交点时，这两个三角形将平面分成5部分；当两个三角形有4个交点时，这两个三角形将平面分成6部分，根据前面给出的规律，在图6的位置画出图形，并补全表格
用2个三角形分平面
情况1图1
情况2图2
情况3图3
情况4图4
情况5图5
情况6图6
交点个数
1
2
3
4
5
增加部分
1
2
3
4
5
能分成的区域数量
3
4
5
6
7
由上图可知：新增加的部分数与新增加的交点个数的关系是

(2)、探究（二）：用3个三角形最多将平面分成几部分？

(3)、探究（三）：用4个三角形最多可以将平面分成几部分？说明理由．
问题解决：用10个三角形最多可以把平面分成部分
建立模型：用n个三角形最多可以把平面分成部分
拓展延伸：用n个m边形最多可以把平面分成部分．

查看试题解析
24. $△ A B C$ 中， $A C = B C = 10 c m$ ， $C D ⊥ A B$ ， $C D = 8 c m$ ，点P以 $1 c m / s$ 的速度由B向A运动，同一时刻点Q、R分别从C、A以 $2 c m / s$ 的速度向B、C运动，当其中一个点运动停止时，其他点的运动也停止．运动时间为 $t (单位 s ， 0 < t < 5)$ ．

(1)、t为何值时， $P R ∥ B C$ ？

(2)、t为何值时，点P在 $B Q$ 的中垂线上？

(3)、是否存在t值，使得 $S_{△ B Q P} ： S_{四边形 C D P Q} = 1 ： 4$ ？若存在求出t值，

查看试题解析

用2个三角形分平面	情况1图1	情况2图2	情况3图3	情况4图4	情况5图5	情况6图6
交点个数	1	2	3	4	5
增加部分	1	2	3	4	5
能分成的区域数量	3	4	5	6	7